Задача №1

Постановка задачи:

На предприятии два цеха выпускают однотипную продукцию. Однако характеристики их оборудования различны, вследствие чего они имеют различные зависимости производительности от вложения средств:

для 1-го цеха ;

для 2-го цеха ;

где y - производительность за неделю; х - количество средств, вложенных за неделю.

Функции остатка средств за неделю равны: для 1-го цеха 0.95 х; для 2-го цеха 0.8 х.

Количество средств, выделенных на оба цеха в течение месяца, составляет 40 единиц. Средства перераспределяются еженедельно и не резервируются. Требуется оптимально распределить средства на планируемый месяц.

Решение:

1. На четвертом шаге условная максимальная производительность равна W₄(k’’’,x4)=max{+}, где k''' может принимать значения от kmin’’’=0.8³∙40=20.48 до kmax’’’=0.95³∙40=34.295.

Построим графики функцииW₄(k’’’,x4), для каждого k’’’ от 20.48 до 34.295 с шагом 1

Найдем максимумы функции W₄(k’’’,x4), для каждого k’’’:

k’’’	x4	W4max
20.48	10,8	44,67
21	11	44,68
22	11,6	44,72
23	12,13	44,74
24	12,66	44,76
25	13,19	44,78
26	13,72	44,8
27	14,24	44,81
28	14,77	44,82
29	15,3	44,83
30	15,82	44,85
31	16,35	44,85
32	16,88	44,86
33	17,41	44,87
34	17,93	44,88
34.295	18,1	44,88

Построим графики зависимости условно максимальной производительности W₄ и условно оптимального управления X4 от k’’’

2) На третьем шаге условная максимальная производительность равна W₃(k’’,x3)=max{+}, где k’’ может принимать значения от kmin’’=0.8²∙40=25.6 до kmax’’=0.95²∙40=36.1.

Построим графики функции W₃(k’’,x3), для каждого k’’ от 25.6 до 36.1 с шагом 1

Найдем максимумы функции W₃(k’’,x3), для каждого k’’:

k’’	x3	W3max
26	12,85	89,52
27	13,34	89,55
28	13,84	89,58
29	14,33	89,61
30	14,82	89,64
31	15,32	89,66
32	15,81	89,68
33	16,3	89,7
34	16,79	89,72
35	17,29	89,73
36	17,78	89,75

Построим графики зависимости условно максимальной производительностиW₃ и условно оптимального управления x3 от k’’

3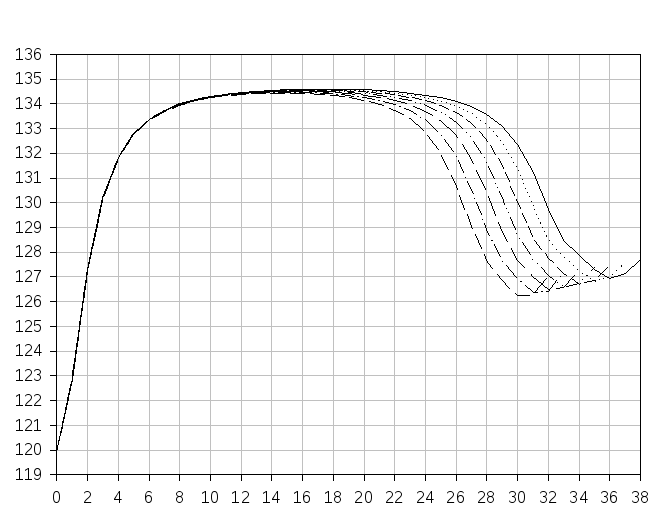) На втором шаге условная максимальная производительность равнаW₂(k’,x2)=max{+}, где k' может принимать значения от kmin’=0.8∙40=32 до kmax’=0.95∙40=38

Построим графики функции W₂(k’,x2), для каждого k’ от 32 до 38 с шагом 1

Найдем максимумы функции W₂(k’,x2), для каждого k’:

k’	x2	W2max
32	14,6	134,43
33	15,05	134,46
34	15,5	134,49
35	15,96	134,52
36	16,41	134,54
37	16,86	134,57
38	17,32	134,59

Построим графики зависимости условно оптимальной производительностиW₂ и условно оптимального управления x2 от k’

4) На первом шаге оптимальная производительность равна W₁(k,x1)=max{+}, где k=40

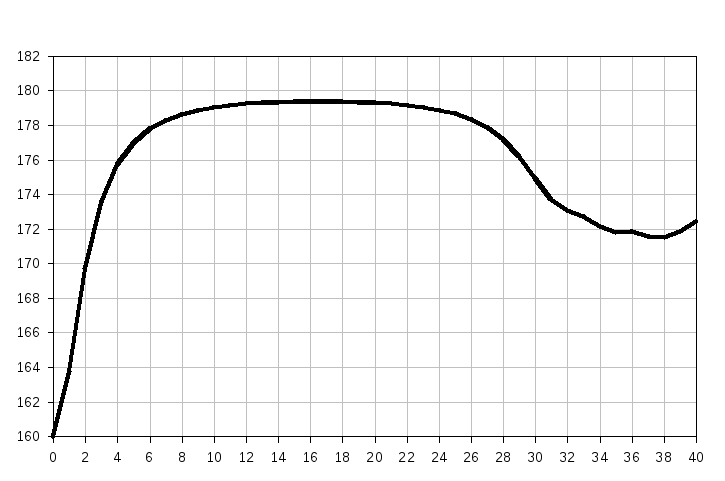Построим график функцииW₁(k,x1), где k=40:

Осуществим прямую прогонку решения задачи, для этого определим на единственной кривой графика W₁(k,x1) максимум, находим оптимальное управление на первом шаге x1=16.54, показывающее, сколько средств надо вкладывать в первый цех, и соответствующую максимальную производительность за месяц W1=179.4, а также количество средств вкладываемы[ во второй цех:

x1’=k-x1, x1’=40-16.54=23.46;

Находим соответствующий запас средств к концу первого шага:

k’=x1∙0.95+(40-x1)∙0.8=34.48;

Входя с этим значением k’ в график x₂(k’) найдем оптимальное управление на втором шаге, показывающее сколько средств нужно вкладывать в первый цех:

x2=15.55;

А также количество средств вкладываемых во второй цех:

x2’=k’-x2=34.48-15.55=18.93;

Остаток средств к концу второго шага будет

k’’=0.95∙x2+0.8∙x2’;

k’’=29.94;

Входя с этим значением k’’ в график x₃(k’’) найдем оптимальное управление на третьем шаге, показывающее сколько средств нужно вкладывать в первый цех:

x3=14.8;

А также количество средств вкладываемых во второй цех:

x3’=k’’-x3=29.94-14.8=15.14;

Остаток средств к концу третьего шага будет

k’’’=0.95∙x3+0.8∙x3’;

k’’’=26.16;

Входя с этим значением k’’’ в график x₄(k’’’) найдем оптимальное управление на третьем шаге, показывающее сколько средств нужно вкладывать в первый цех:

x4=13.8;

А также количество средств вкладываемых во второй цех:

x4’=k’’’-x4=26.16-13.8=12.39;

Таким образом, можно сформулировать следующие рекомендации по оптимальному распределению средств. Из имеющегося в начале месяца запаса средств k=40 усл. ед. и остающихся средств в конце каждой недели нужно вкладывать по неделям в цеха I и II следующие суммы:

Недели	1-я	2-я	3-я	4-я
I цех	16.54	15.55	14.8	13.8
II цех	23.46	18.93	15.14	12.39

При таком планировании будет получена максимальная производительность за месяц, равная W₁max=179.4 усл. ед.

Определим остаток средств на конец месяца: 13.8∙0.95+12.39∙0.8=23 усл. ед.

Задача №2.

Постановка задачи:

Эту же продукцию выпускают два других предприятия, на которых объем выпуска продукции в месяц составляет в среднем 100 и 150 ед. Общее количество продукции трех предприятий, выпускаемой за месяц, необходимо перевезти в шесть городов в пропорции 1:2:3:4:5:6. Транспортные расходы на перевозку единицы готовой продукции (в млн. руб.) представлены в таблице.

	B1	B2	B3	B4	B5	B6
A1	4	6	4.5	5	8	1
A2	6	5	8	7	2	1
A3	7	2	6	3	6	3

Требуется: найти план перевозок, оптимальный по критерию стоимости;

Математическое представление задачи:

целевая функция: ΣCijXij → min;

ограничения: Ai = ΣjXij, i=[1,3], j=[1,6];

Ki*X0 = ΣiXij, i= [1,3], j= [1,6];

Табличное представление исходных данных:

ПО\ПН	B1	B2	B3	B4	B5	B6	Запасы
A1	4	6	4.5	5	8	1	179
A2	6	5	8	7	2	1	100
A3	7	2	6	3	6	3	150
Потребности	20	41	61	82	102	123	429

Решение в ППП МикроЛП:

Файл данных:

NAME

NAME

ROWS

N Z

E A1

E A2

E A3

E B1

E B2

E B3

E B4

E B5

E B6

N COBJ

COLUMNS

X11 Z 4.0

X11 A1 1.0

X11 B1 1.0

X11 COBJ 0.0

X12 Z 6.0

X12 A1 1.0

X12 B2 1.0

X12 COBJ 0.0

X13 Z 4.5

X13 A1 1.0

X13 B3 1.0

X13 COBJ 0.0

X14 Z 5.0

X14 A1 1.0

X14 B4 1.0

X14 COBJ 0.0

X15 Z 8.0

X15 A1 1.0

X15 B5 1.0

X15 COBJ 0.0

X16 Z 1.0

X16 A1 1.0

X16 B6 1.0

X16 COBJ 0.0

X21 Z 6.0

X21 A2 1.0

X21 B1 1.0

X21 COBJ 0.0

X22 Z 5.0

X22 A2 1.0

X22 B2 1.0

X22 COBJ 0.0

X23 Z 8.0

X23 A2 1.0

X23 B3 1.0

X23 COBJ 0.0

X24 Z 7.0

X24 A2 1.0

X24 B4 1.0

X24 COBJ 0.0

X25 Z 2.0

X25 A2 1.0

X25 B5 1.0

X25 COBJ 0.0

X26 Z 1.0

X26 A2 1.0

X26 B6 1.0

X26 COBJ 0.0

X31 Z 7.0

X31 A3 1.0

X31 B1 1.0

X31 COBJ 0.0

X32 Z 2.0

X32 A3 1.0

X32 B2 1.0

X32 COBJ 0.0

X33 Z 6.0

X33 A3 1.0

X33 B3 1.0

X33 COBJ 0.0

X34 Z 3.0

X34 A3 1.0

X34 B4 1.0

X34 COBJ 0.0

X35 Z 6.0

X35 A3 1.0

X35 B5 1.0

X35 COBJ 0.0

X36 Z 3.0

X36 A3 1.0

X36 B6 1.0

X36 COBJ 0.0

RHS

R1 A1 179.0

R1 A2 100.0

R1 A3 150.0

R1 B1 20.0

R1 B2 41.0

R1 B3 61.0

R1 B4 82.0

R1 B5 102.0

R1 B6 123.0

ENDATA

Результат решения:

0итер вв . выв. оценка функционал недопустим. число,длина

прямые,дв. столб. файла

0 0 0 .0000 858.00000 9 0 0 0

1 17 2 1.0000 612.00000 8 0 1 5

2 25 4 2.0000 530.00000 7 0 2 9

3 27 6 1.0000 366.00000 6 0 3 14

4 22 9 2.0000 166.00000 5 0 4 18

5 26 7 3.0000 112.00000 4 0 5 23

6 14 10 .5000 44.00000 3 0 6 30

7 28 8 1.0000 40.00000 2 0 7 36

0дв. алгоритм прекращен

8 12 3 1.5000 1055.00000 0 0 8 44

0оптимальное решение.

8 0 3 .0000 1055.00000 0 0 8 44

секция строк

строка N тип доп.переменная нижняя граница верхняя граница дв. оценка

Z 1 BS -1055.00000 (NONE) (NONE) 1.00000

A1 2 FX . 179.00000 179.00000 -4.00000

A2 3 FX . 100.00000 100.00000 -1.50000

A3 4 FX . 150.00000 150.00000 -5.50000

B1 5 BS . 20.00000 20.00000 .

B2 6 FX . 41.00000 41.00000 3.50000

B3 7 FX . 61.00000 61.00000 -.50000

B4 8 FX . 82.00000 82.00000 2.50000

B5 9 FX . 102.00000 102.00000 -.50000

B6 10 FX . 123.00000 123.00000 3.00000

COBJ 11 BS . (NONE) (NONE) .

секция столбцов

столбец N тип переменная нижняя граница верхняя граница дв. оценка

X11 12 BS 20.00000 . (NONE) .

X12 13 LL . . (NONE) 5.50000

X13 14 BS 36.00000 . (NONE) .

X14 15 LL . . (NONE) 3.50000

X15 16 LL . . (NONE) 3.50000

X16 17 BS 123.00000 . (NONE) .

X21 18 LL . . (NONE) 4.50000

X22 19 LL . . (NONE) 7.00000

X23 20 LL . . (NONE) 6.00000

X24 21 LL . . (NONE) 8.00000

X25 22 BS 100.00000 . (NONE) .

X26 23 LL . . (NONE) 2.50000

X31 24 LL . . (NONE) 1.50000

X32 25 BS 41.00000 . (NONE) .

X33 26 BS 25.00000 . (NONE) .

X34 27 BS 82.00000 . (NONE) .

X35 28 BS 2.00000 . (NONE) .

X36 29 LL . . (NONE) .50000

Вывод данных завершен

1 24 LL . . (NONE) 1.50000

X32

План перевозок, оптимальный по критерию стоимости представлен в данной таблице:

ПО\ПН	В1	В2	В3	В4	В5	В6	Запасы
А1	20 4	0 6	36 4,5	0 5	0 8	123 1	179
А2	0 6	0 5	0 8	0 7	100 2	0 1	100
А3	0 7	41 2	25 6	82 3	2 6	0 3	150
Потребности	20	41	61	82	102	123	429

Мы получили оптимальный план перевозок, стоимость перевозки при таком решении f(x)=20∙4+41∙2+36∙4.5+25∙6+82∙3+100∙2+2∙6+123=1055 усл. ед.