Задача по тпр №4 (вар 6)

[ PASTE HERE ]

Задача 4-6. Из теоретических соображений известно, что связь между зависимой переменной y и переменной x можно описать двухпараметрической функцией . Значения параметров a и b определяются в соответствии с критерием наименьших квадратов на основе экспериментальных данных, представленных в таблице. Найти a и b.

Метод решения: Метод Хука-Дживса

x	0,2	0,4	0,7	0,9
y	0,4	1,0	1,0	0,8

Решение:

Целевой функцией в этой задаче будет сумма квадратов разностей , приведённых в таблице и , рассчитываемая по формуле:

Решение с помощью программы на языке Си:

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

//GloBal VariAbles

float step;

int a_direction, b_direction;

float a, b, new_a, new_b, old_a, old_b, e = 0.001;

int i1,i2;

float getWvalue(float a, float b);

void direction_search(float a, float b);

void main(void){

//iniTial valUes

step = 0.1;

a = 2.1;

b =-0.4;

i2 = 0;

while( step >= e){

direction_search(a,b);

new_a = a + (a_direction*step);

new_b = b + (b_direction*step);

i1 = i2;

while( getWvalue(new_a,new_b) < getWvalue(a,b) ){

old_a = a;

old_b = b;

a = new_a;

b = new_b;

new_a = 2*a - old_a;

new_b = 2*b - old_b;

i2++;

}

if(i1==i2)

step = step/2;

i2 = 0;

}

printf("Result: a = %f\tb = %f\n", a, b);

printf(" W = %f\n", getWvalue(a,b));

}

void direction_search(float a, float b){

if( getWvalue(a+step,b) < getWvalue(a,b) )

a_direction = 1;

else // if >=

a_direction = 0;

if( getWvalue(a-step,b) < getWvalue(a,b) )

a_direction = -1;

if( getWvalue(a,b+step) < getWvalue(a,b) )

b_direction = 1;

else // if >=

b_direction = 0;

if( getWvalue(a,b-step) < getWvalue(a,b) )

b_direction = -1;

}

// W function

float getWvalue(float a, float b){

return (

pow((0.4-(sin(0.04*a)/(1+(0.2*b)))),2) +pow((1-(sin(0.16*a)/(1+(0.4*b)))),2) +

pow((1-(sin(0.49*a)/(1+(0.7*b)))),2) + pow((0.8-(sin(0.81*a)/(1+(0.9*b)))),2));

}

Программа вывела: a=3.15, b=-0.23, W(a,b)=0.337.

Проверка с помощью Excel дала следующие результаты:

1) С помощью функции «Поиск решения»:

a	3,147415	W	0,337423
b	-0,23209

2) Таблица:

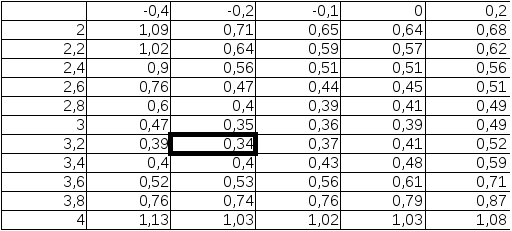
Ответ: a=3.15, b=-0.23.