Задача по ТПР №4 (вар 3)

[ PASTE HERE ]

Отчет по практической работе №4

“Безусловная однопараметрическая оптимизация”.

(4-3)

Задача: Определить место строительства предприятия между двумя магазинами, расстояние между которыми 120 км, и размер поставок в каждый из пунктов, если выпуск продукции завода составляет 200 единиц. Зависимость продажной цены единицы продукции в каждом из магазинов от объема поставок V_i и затрат на перевозку единицы продукции от расстояния S_i (в км.) между предприятием и магазином заданы в таблице.

Вариант	Пункт сбыта	Цена	Затраты на перевозку	Метод решения
4-3	1 2	490-0.7*V1 500-0.8*V2	15+0.3*S1 15+0.2*S2	Метод Пауэлла

Решение:

В качестве показателя эффективности целесообразно взять прибыль от продаж единиц продукции в магазины. Тогда прибыль от поставок в магазин 1:

(490-0.7*V₁-15-0.3*S₁)*V₁,

Прибыль от поставок в магазин 2:

(500-0.8*V₂-15-0.2*S₂)*V₂

Учитывая, что расстояние между городами равно 120 км., а выпуск продукции – 200 единиц получим:

S₂=120-S₁, V₂=200-V₁

Тогда целевая функция для определения максимальной прибыли:

(490-0.7*V₁-15-0.3*S₁)*V₁+(500-0.8*V₂-15-0.2*S₂)*V₂ -> max

После преобразований получим:

-1.5V₁²+334V₁+40S₁-0.5S₁V₁+60200 -> max (1)

где V₁, S₁ - объем поставок и затраты на перевозку единицы продукции в магазин 1.

Алгоритм метода Пауэлла:

Шаг 1. Задать начальную точку x₀ и систему N линейно независимых направлений s_i; целесообразно принять s_i=e_i, i=1,2,...,N.

Шаг 2. Минимизировать W(x) при последовательном движении по N+1 направлениям; при этом полученная ранее точка минимума берется в качестве исходной, а направление s_N используется как при первом, так и при последнем поиске.

Шаг 3. Определить новое сопряженное направление с помощью обобщенного свойства параллельного подпространства.

Шаг 4. Заменить s₁ на s₂ и так далее (s_i=s_i+1). Заменить s_N сопряженным направлением. Перейти к шагу 2.

Шаг 5. По определенному на 3-ем шаге направлению провести одномерный поиск. Результат – найденный оптимум функции.

Программа:

Далее приведен листинг программы на языке С, реализующей метод Пауэлла:

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

// Точность

#define EPSILON 0.001

// Новое направление

float s[2];

float e1[2], e2[2];

float W(float x, float y);

float WW(float t, float *x);

float maxHalf(float *x);

// Целевая функция

float W(float x, float y) {

return -1.5*x*x+334*x+40*y-0.5*x*y+60200;

}

// Целевая функция по направлению

float WW(float t, float *m) {

float x, y;

x=m[0]+s[0]*t;

y=m[1]+s[1]*t;

return W(x,y);

}

// Метод деления отрезка пополам

float maxHalf(float *x) {

int i;

float a=0,b=120;

float x1,x2,xm;

float len;

xm=(a+b)/2; len=b-a;

while (fabs(len) >= EPSILON) {

x1=a+len/4;

x2=b-len/4;

if (WW(x1,x) > WW(xm,x)) {

b=xm; xm=x1;

}

else if (WW(x2,x) > WW(xm,x)) {

a=xm; xm=x2;

} else {

a=x1; b=x2;

}

len/=2;

}

return x1;

}

// Главная программа

int main(void) {

// Точки

float x0[2],x1[2],x2[2],x3[2],x4[2];

int i;

// Минимум соответствующей одномерной задачи оптимизации

float t;

// Расстояние между x1 и x3

float L;

// Задание единичных векторов

e1[0]=1; e1[1]=0;

e2[0]=0; e2[1]=1;

// Начальная точка

x0[0]=90; x0[1]=0;

for (i=0; i<2; i++)

x1[i]=x2[i]=x3[i]=x4[i]=0;

// Пока не достигнем заданной точности повторять основные шаги

do {

for (i=0; i<2; i++) s[i]=e2[i];

t=maxHalf(x0);

for (i=0; i<2; i++) {

x1[i]=x0[i]+s[i]*t;

s[i]=e1[i];

}

t=maxHalf(x1);

for (i=0; i<2; i++) {

x2[i]=x1[i]+s[i]*t;

s[i]=e2[i];

}

t=maxHalf(x2);

for (i=0; i<2; i++) {

x3[i]=x2[i]+s[i]*t;

}

L=sqrt(pow(x3[0]-x1[0],2)+pow(x3[1]-x1[1],2)+pow(x3[2]-x1[2],2));

for (i=0; i<2; i++) {

e1[i]=e2[i];

e2[i]=(x3[i]-x1[i])/L;

}

t=maxHalf(x3);

for (i=0; i<2; i++) {

x4[i]=x3[i]+s[i]*t;

x0[i]=x4[i];

}

} while (L > EPSILON);

// Вывод результатов

printf("V1 = %1.8f\n", x3[0]);

printf("S1 = %1.8f\n", x3[1]);

printf("W = %1.8f\n", W(x3[0],x3[1]));

getchar();

return 0;

}

Программа выдала следующие результаты:

V1 = 111.3338

S1 = 0.001831

W = 78792.63798

Необходимо отметить, что существенное значение имеет выбор начальной точки.

Решение с помощью функции Excel «Поиск решения» и тестовый график:

Установив необходимые ограничения, получаем следующие результаты:

V1	S1	W
111.3333	0	78792.66667

Также в Mathcad был построен тестовый график поверхности:

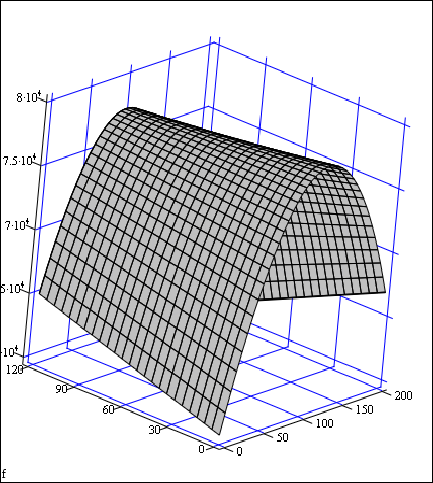
С помощью пакета Mathcad было получено следующее решение:

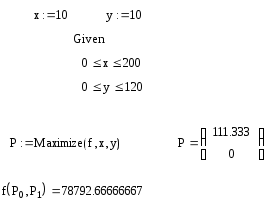
Видно, что результаты практически совпадают, что говорит о достоверности вычислений.

Ответ: Прибыль будет максимальной, если построить предприятие на расстоянии 0 км. от магазина 1 (то есть в том же месте, где и магазин 1) и поставлять в магазин 1 – 111.3 единиц продукции, а в магазин 2 –88.7 единиц. Тогда прибыль составит 78792.7 денежных единиц.

4