Санкт-Петербургский государственный электротехнический

университет «ЛЭТИ» имени В.И. Ульянова (Ленина)

Кафедра АСОИУ

Курсовая работа

по дисциплине «Теория и методы принятия решений»

Вариант № 7.10

Выполнила:.

Группа:

Факультет: ОФ

Проверил: Яшин А.И

Санкт-Петербург

2006

Задача№1

На предприятии вкладываются средства в развитие двух цехов. Функции дохода от вложенных средств для 1-го и 2 –го цехов различны и представлены следующими зависимостями:

для 1-го цеха y=120+(1,8*x+25)^1/2;

для 2-го цеха y=140+(2,0*x+30)^1/2;

Где у- доход за 1 квартал (млн. руб)

x- количество средств, вложенных за 1 квартал равны:

для 1-го цеха Q=0,8*x;

для 2-го цеха L=09*x.

Количества средств, выделяемых на развитие обоих цехов в течение года, составляет 140 единиц. Средства перераспределяются поквартально и не резервируются. Требуется оптимально распределить между двумя цехами средства на планируемый год.

4 шаг

Q=0,8^3*140

L=0,9^3*140

W4(k)=120+(1,8*X+25)^1/2)+140(2,0*(k-X)+30)^(1/2)=

260+(1,8*X+25)^1/2)+(2,0*(k-X)+30)^(1/2)

Q	89,6
L	102,06
KSR	95,83
K1	98,945
K2	92,715

x	K 71,68	k 79,275	k 86,87	k 94,465	K 102,06
	W4(x)	W4(x)	W4(x)	W4(x)	W4(x)
0	351,68	359,275	366,87	374,465	373,4397
10,206	343,0597	350,6547	358,2497	365,8447	364,5056
20,412	334,1256	341,7206	349,3156	356,9106	355,3926
30,618	325,0126	332,6076	340,2026	347,7976	346,1599
40,824	315,7799	323,3749	330,9699	338,5649	336,8399
51,03	306,4599	314,0549	321,6499	329,2449	327,4526
61,236	297,0726	304,6676	312,2626	319,8576	318,0114
71,442	287,6314	295,2264	302,8214	310,4164	308,5256
81,648	278,1456	285,7406	293,3356	300,9306	299,0023
91,854	268,6223	276,2173	283,8123	291,4073	289,4467
102,06	259,0667	266,6617	274,2567	281,8517	373,4397

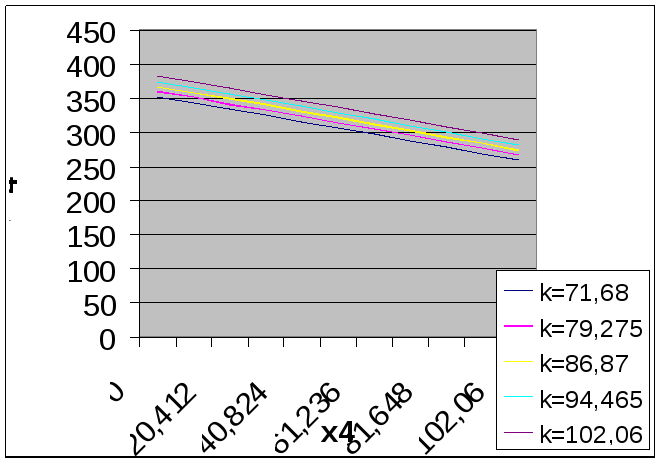
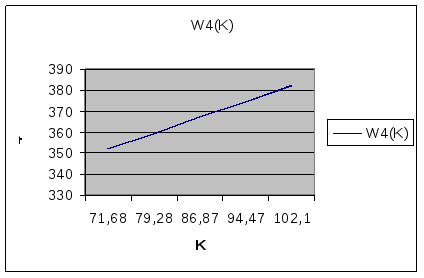
3.Шаг

Q	89,6
L	113,4
KSR	101,5
K1	95,55
K2	107,45

W3(k) =260+(1,8*X+25)^1/2)+(2,0*(k-X)+30)^(1/2)+W4(K ‘)

K’=0,8*x+0,9*(K-X)

x	K 89,6	k 95,55	K 101,5	k 107,45	k 113,4
	W3(x)	W3(x)	W3(x)	W3(x)	W3(x)
0	558,2941	558,419	559,8486	560,5962	561,326
10,745	559,9662	552,1894	561,6111	562,3988	563,1656
21,49	560,8529	553,9613	562,6066	563,4415	564,2518
32,235	561,2248	555,28	563,1126	564,0046	564,8668
42,98	561,1712	556,251	563,2304	564,1935	565,1193
53,725	560,7001	556,9099	562,9903	564,0453	565,0517
64,47	559,7431	557,2394	562,3717	563,553	564,6666
75,215	558,075	557,1398	561,2878	562,66	563,9277
85,96	554,3907	556,2047	559,4847	561,2118	562,7344
96,705	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	558,6588	560,8028
107,45	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!

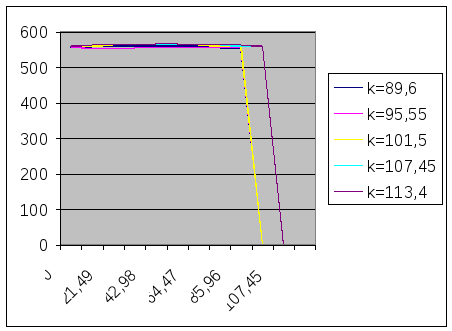
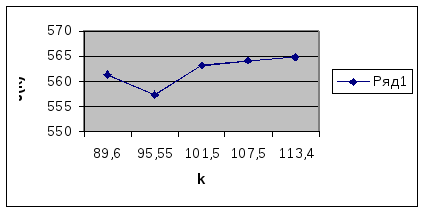
2.Шаг

Q	144
L	162
KSR	153
K1	157,5
K2	148,5

W2 =260+(1,8*X+25)^1/2)+(2,0*(k-X)+30)^(1/2)+W3 (K’)

K’=0,8*x+0,9*(K-X)

x	K 144	k 148,5	K 153	k 157,5	k 162
	W2x)	W2x)	W2x)	W2x)	W2x)
0	564,8384	565,3255	565,806	566,2801	566,7481
16,2	567,542	568,0585	568,5672	569,0683	569,5623
32,4	568,9303	569,4825	570,0251	570,5586	571,0833
48,6	569,5718	570,1683	570,7528	571,3259	571,8883
64,8	569,6379	570,2919	570,93	571,5534	572,1631
81	569,1637	569,8966	570,6073	571,2977	571,9695
97,2	568,08	568,9323	569,7497	570,5363	571,2955
113,4	566,1257	567,1986	568,2013	569,1467	570,0441
129,6	561,8302	563,8662	565,4091	566,7323	567,9186
145,8	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	562,724
162	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!	#ЧИСЛО!

1.Шаг

Ko=140 ед.

X	W1(K)
0	564,3997
18	567,2747
36	568,6206
54	569,0965
72	568,8693
90	567,9165
108	565,983
126	561,5431
144	#ЧИСЛО!
162	#ЧИСЛО!
180	#ЧИСЛО!

W(max)=W1(140)=569,0965 при х1=54 =>

Запас средств после 1 шага: K1*=0,8*54+0,9*(140-54)=120,6

Зайдём с этим значением в график x2(K) и найдём оптимальное управление на 2-ом шаге x2=64,8 =>K2*=102,06

Зайдём с этим значением в график x3K) и найдём оптимальное управление на 3ом шаге x3=42,98 =>K3*=87,556

Зайдём с этим значением в график x4(k) найдём оптимальное управление на 4-ом шаге

X4=0 =>K4=78,8

Таким образом, можно сформулировать следующие рекомендации по вложению средств.

Из имеющегося в начале запаса Ко=140 и остающихся средств в конце каждого квартала нужно поквартально вкладывать следующие суммы в 1 и 2 цех.

Отрасли	1 квартал	2 квартал	3 квартал	4 квартал
1	54	64,8	42,98	0
2	86	55,8	59,08	87,556