Point 4. Integration by parts
Theorem 3. Let
be two continuously differentiable functions. The next formula
(formula of integration by parts)
is true
(
12 )
■It’s known that the differential of a product of two functions equals
.
Integrating this equality we obtain
.■
According tо the formula (7) we represent the expression under the integral sign in the form of a product of two functions, namely u and dv. Then we differentiate the first function and integrate the second one.
Ex. 19.
.
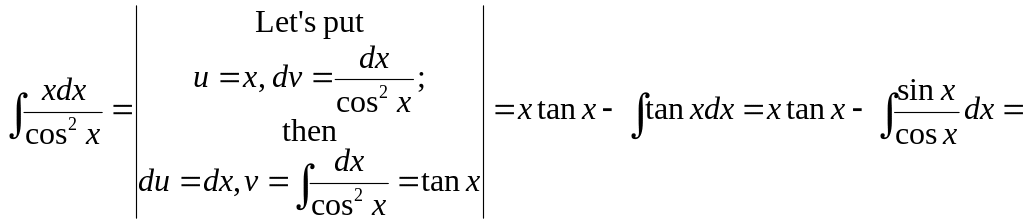
Ex. 20.
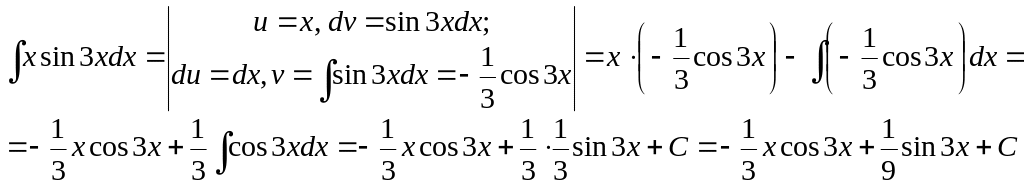
Note 5. Integration by parts by necessity can be performed several times.
Ex. 21.
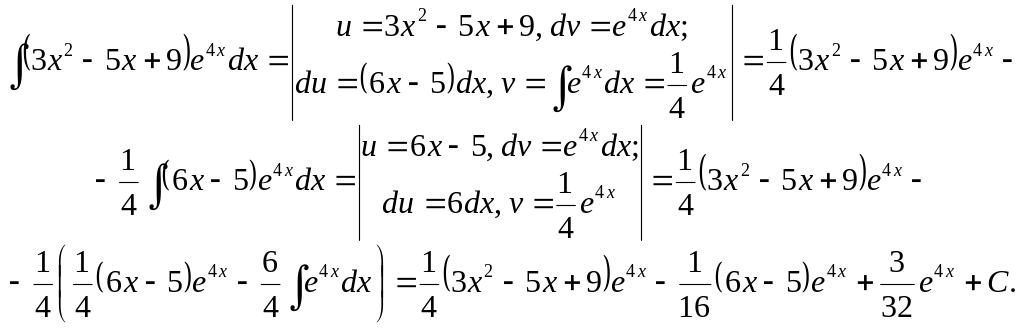
Note 6. Sometimes integration by parts leads to an equation in a required integral
Ex. 22.
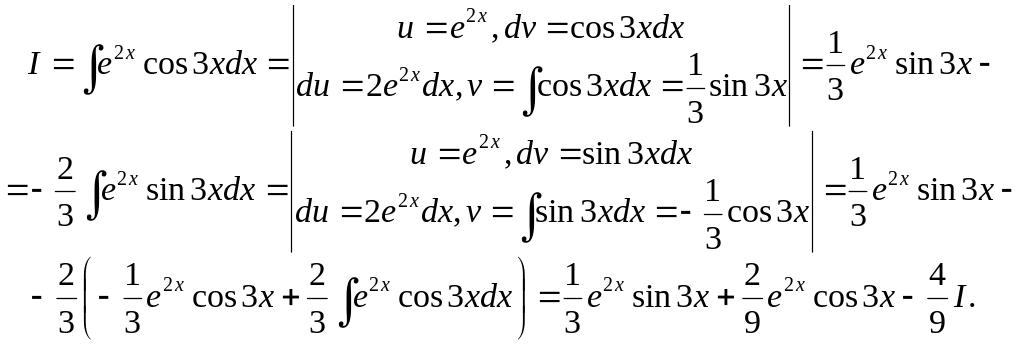
We’ve got the equation in the sought integral I and hence
Ex. 23.
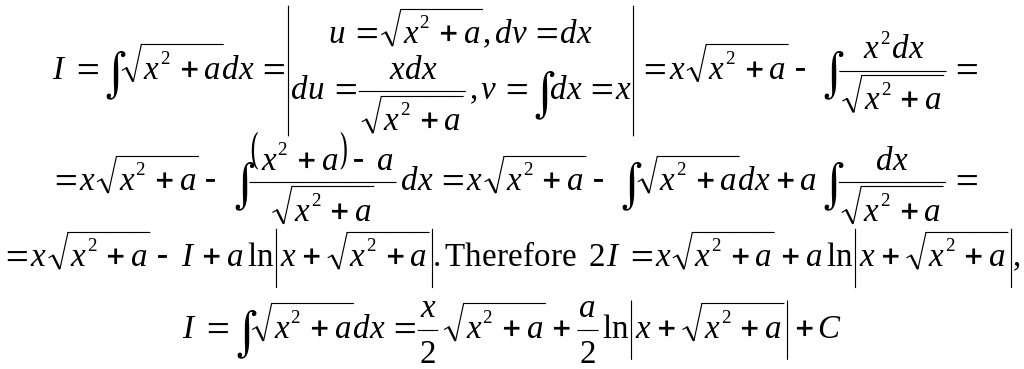
Note 7. There are
no general rules to choose
.
But in some cases one can give certain advices.
In the cases of integrals
,
where
is a polynomial, it’s well to put
.
In the cases of integrals
it’s well to put
.
Ex. 24.
.
Lecture no.20. Classes of integrable functions
POINT 1. RATIONAL FRACTIONS (RATIONAL FUNCTIONS)
POINT 2. TRIGONOMETRIC FUNCTIONS
POINT 3. IRRATIONAL FUNCTIONS
Point 1. Rational functions (rational fractions)
Def. 1. Rational function (rationas fraction) is called a function which can be represented as a ratio of two polynomials
.
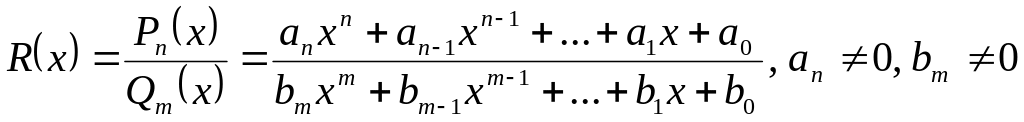( 1 )
Def. 2. Rational
function (rationas fraction) (1) is called
proper one
if
and improper
otherwise (
).
Theorem 1 (extraction of integer part of an improper rational function). Every improper rational function can be represented as a sum of some polynomial (so-called integer part) and a proper rational function.
■Let
.
Dividing the numerator
by the denominator
we get
where
polynomials
are a quotient and a remainder respectively and
is a proper rational function.■
Ex. 1. Extract an integer part of an improper rational fraction
a) The first (theoretical) way. After division of
by
we get
b) The second way. Subtracting and adding 1 in the numerator we’ll have
There are partial [simplest, elementary] fractions of 1- 4 types.
1.
;
2.
;
3.
;
4.
.
We’ve
integrated the fractions 1, 3 in the Point 2 of preceding lecture
(ex. 14, 16, formulas (7), (10) and (11)). To integrate the fraction
2 we can put
.
Integration of the fraction 4 with the help of the substitution
leads to a linear combination of a simple integral
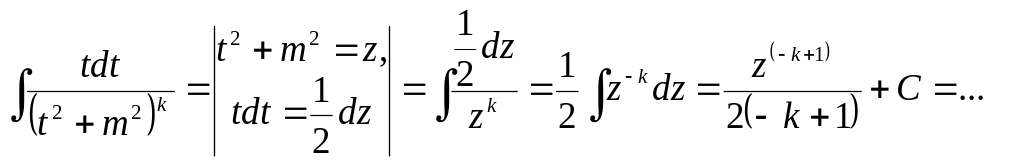
and the next one
.
As
to evaluation of this latter see textbooks. For small values of k
(
)
one can use the next substitution:
.
Ex. 2.
.
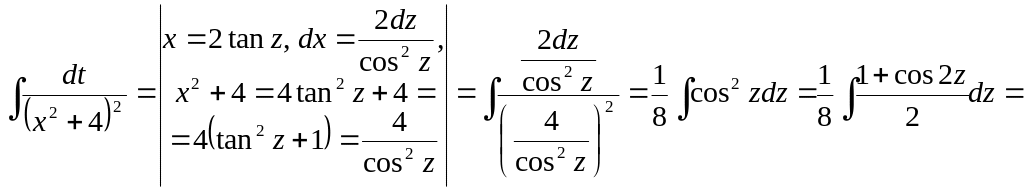
Thus we can say that we able to integrate partial fractions 1 – 4.
Theorem 2 (a partial decomposition of a proper rational function). Every proper rational function can be represented as a linear combination of partial fractions.
For example
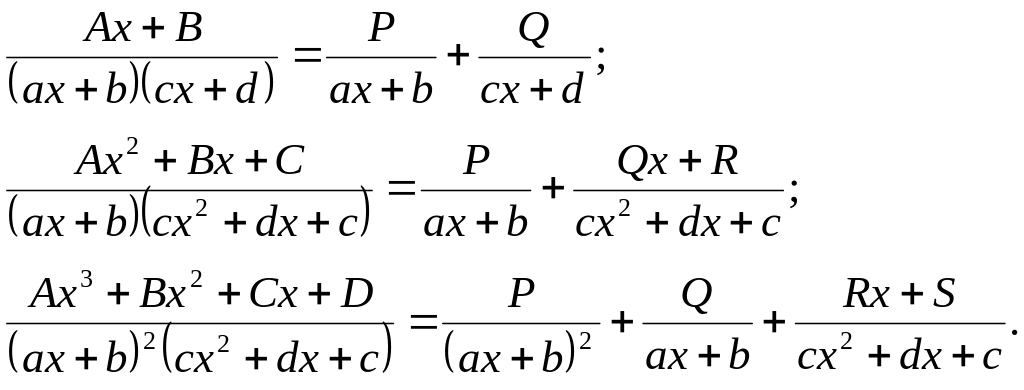
Here
are some unknown numbers (undetermined coefficients), which one can
find by so-called method of undetermined
coefficients.
Corollary. Every rational function can be integrated by virtue of the linear property of indefinite integral.
Rule of integration of a rational function. To integrate a rational function it’s necessary:
1. To extract an integer part of the function if it is improper one.
2. To factorize the denominator of obtained proper function into a product of polynomials of degree not higher than two.
3. To make a partial decomposition of the proper function.
4. To integrate all the terms of the obtained algebraic sum.
5. To write an answer.
Ex. 3.
.
Ex. 4. Evaluate the indefinite integral
.
1 step (factorizing the denominator of the proper rational function).
.
2 step (a partial decomposition of the proper function).
Let’s
assign two particular values to x
in (*), namely
.
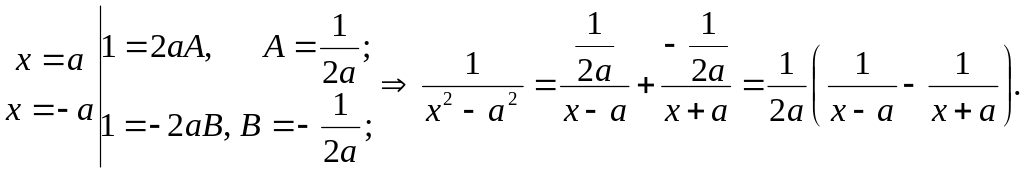
3 step (integration of the given function by integration of its partial decomposition).
Ex. 5. Calculate the next indefinite integral
1 step (a partial decomposition of the proper rational function with factorized denominator).
,
.
(**)
Assigning tree
arbitrary values to x in
(**), for example
,
we get a system of linear equations in
,
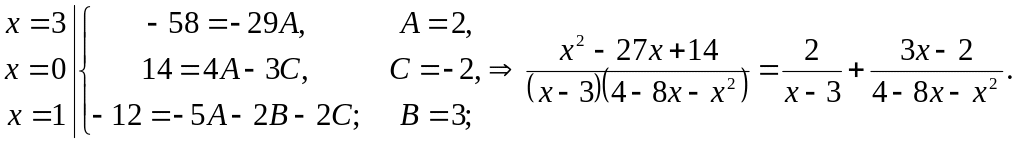
2 step (integration of all the terms of obtained partial decomposition of the integrand)
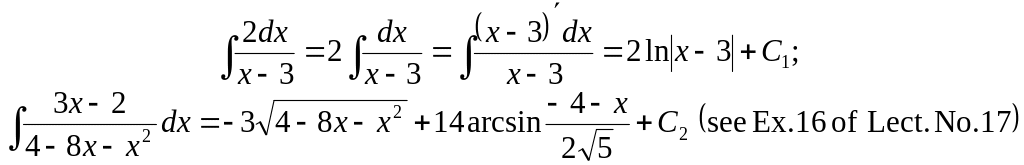
Answer.
