Lecture no. 24. Double integral

POINT 1. DOUBLE INTEGRAL

POINT 2. EVALUATION OF A DOUBLE INTEGRAL IN CARTESIAN COORDINATES

POINT 3. IMPROPER DOUBLE INTEGRAL. POISSON’S FORMULA

Point 1. Double integral

Def. 1. Let a function of two variables be given in a some domain D of the -plane (fig. 1).

1. We divide the domain into n parts with areas and diameters .

2. We take arbitrary point in every part , find the value of the function at this point and multiply it by the area of .

3. We add all these products Fig. 1 and get an integral sum

.

4. Let and . If there exists the limit of the integral sum , then this limit is called the double integral of the function over the domain D and is denoted by

( 1 )

Theorem 1 (existence of a double integral). If a function is continuous in a domain D then its double integral over D exists.

It is evident that for a double integral gives the area of the domain D,

. ( 2 )

Mechanic sense of a double integral. If is the surface density of a plate , then its mass equals the next double integral

( 3 )

■An element of the mass

;

it is the mass of the element with the area and with a constant surface density (fig. 2). Sum of all these elements gives the mass of the plate which is re- Fig. 2 presented by a double integral (3).■

Def. 2. A cylindrical body [a curvilinear cylinder] is called a body bounded:

a) above by a surface ;

b) below by a domain D;

c) aside by a cylindrical surface with the generatrix parallel to -axis (fig. 3).

Geometric sense of a double integral. The volume of a cylindrical body equals the double Fig. 3 Fig. 4 integral

. ( 4 )

■An element of the volume

is the volume of a right circular cylinder with the base of the area and the height (fig. 4). The volume of a cylindrical body is the sum of all these elements and is represented by the double integral (4).■

Properties of a double integral are the same as for a definite integral.

For example:

1 (linearity). For any functions and any constants

.

2 (additivity). If a domain is divided into two disjoint parts , (fig. 5), then

. Fig. 5

Point 2. Evaluation of a double integral in cartesian coordinates

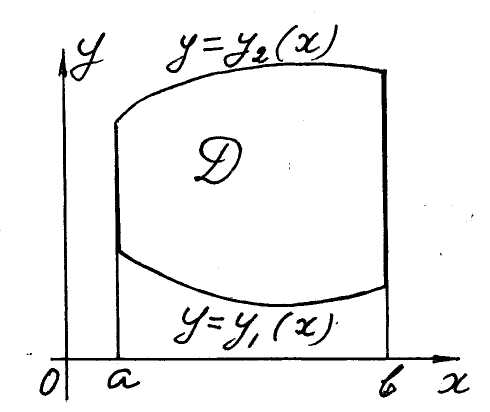Def. 3. A domain D is called a domain of the first type if it is bounded (see fig. 6):

a) from the left by a straight line ;

b) from the right by a straight line ;

c) below by a line ;

d) above by a line , Fig. 6 .

A double integral over a domain of the first type is calculated by a formula

. ( 5 )

Correspondingly to this formula we integrate at first with Fig. 7 respect to y from to , that is calculate an inner integral

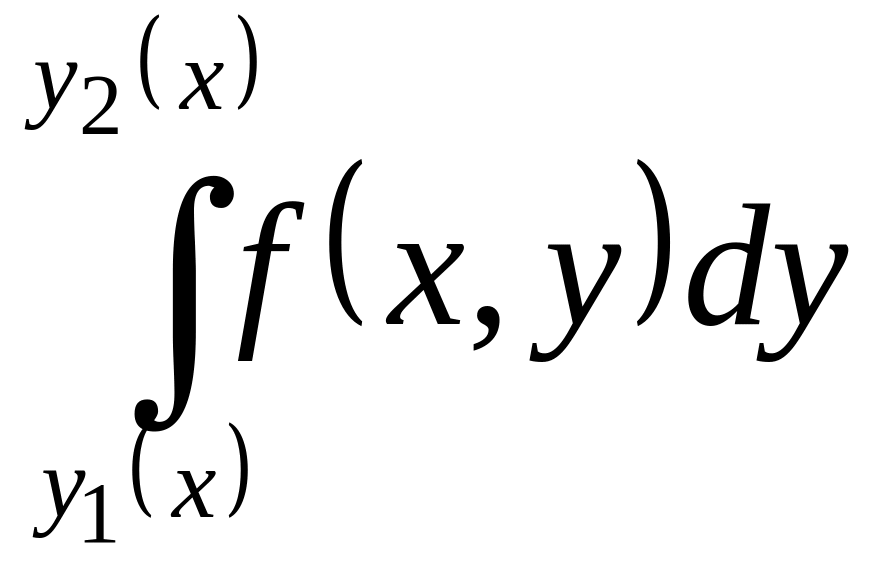, and then we integrate the result with respect to x from a to b.

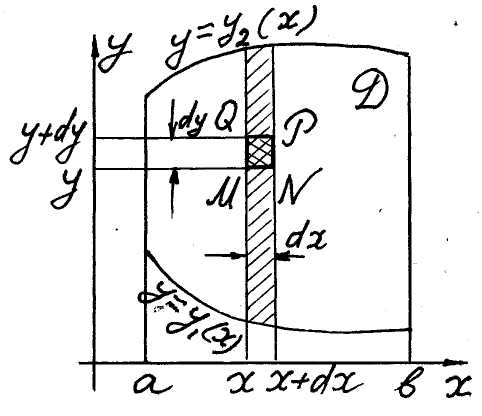
■We’ll prove the formula (5) proceeding from the mechanic sense of a double integral. Let the integrand be the surface density of a plate, defi-ned by the figure (fig. 6). Hence the mass of the plate equals the double integral

.

Now we’ll find the same mass by the other way and compare the results. The mass of the element of the plate between and (fig. 7) equals . Adding all such the masses from to we find the mass of the hatched strip (fig. 7), namely

.

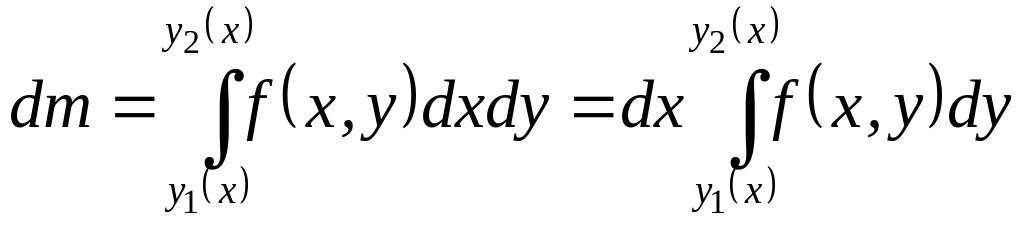Adding finally the masses of all such the strips from to we find the mass of the whole plate that is

.

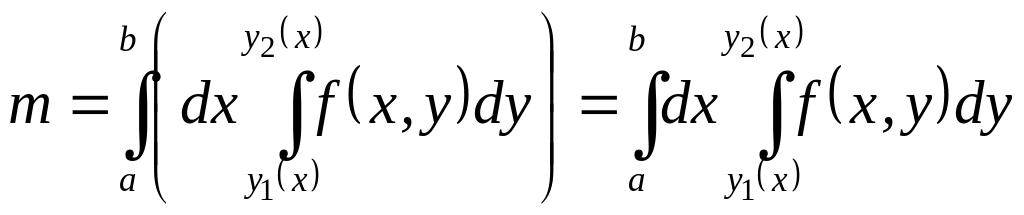Comparing of two results of the mass calculating proves validity of the formula (5).■

Note 1. Integral with respect to x from a to b is called that exterior [external]. The right side of the formula (5) is called the repeated integral.

Def. 4. A domain D is called a domain of the se-cond type if it is bounded (see fig. 8):

a) below by a straight line ; b) above by a a straight line ; c) from the left by a line ; Fig. 8 d) from the right by a line ,

.

A double integral over a domain D of the second type is calculated by a formula

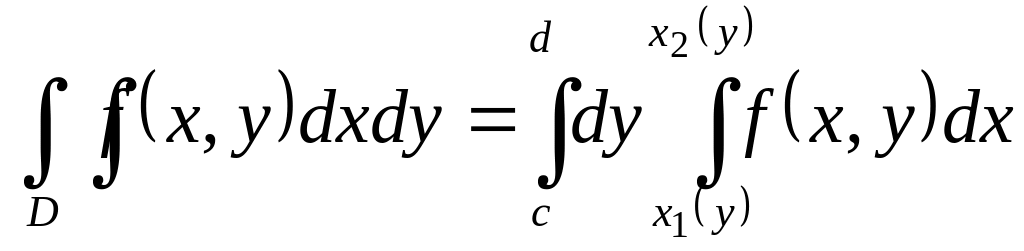. ( 6 )

At first we calculate an inner integral

,

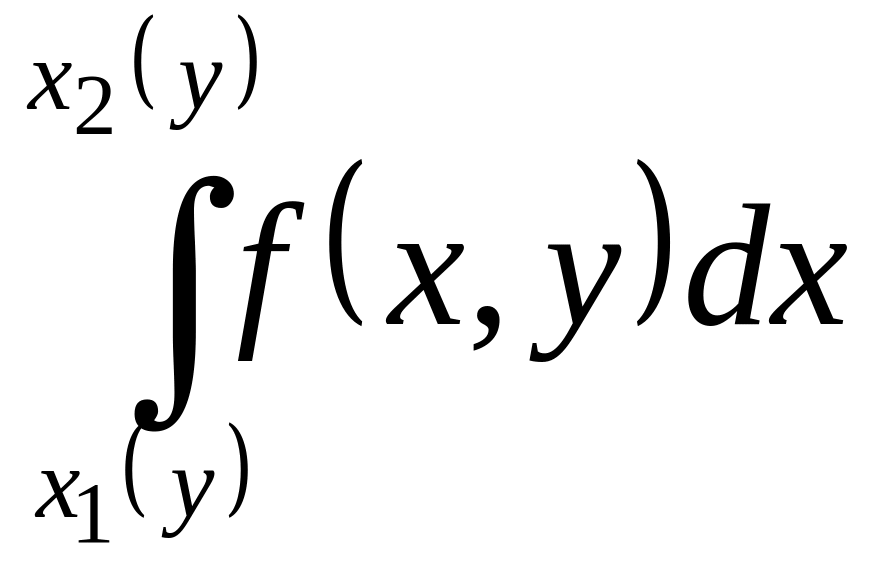that is integrate with respect to x from to , and then we integrate the result with respect to y from c to d.

■Prove this formula yourselves.■

Ex. 1. Let a domain of integration is a rectangle

with the sides parallel to Ox-, Oy-axes (fig. 9). The rec-tangle is the domain of the first and second types, there- Fig. 9 fore we can use both formulas (5) and (6),

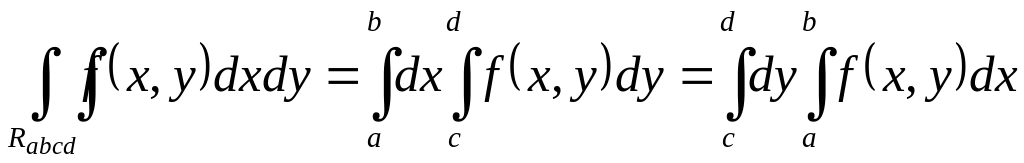. ( 7 )

The formula (6) means that in the case of the rectangle we can integrate in any order. But one of orders of integration can lead to easier calculations than the other one.

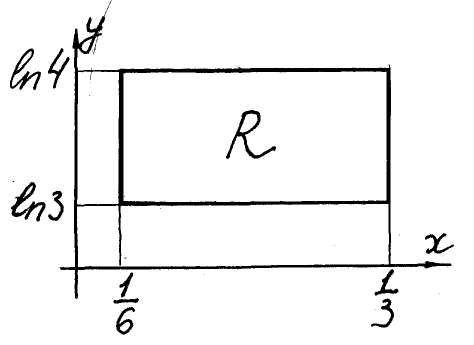
Ex. 2. Find the mass of a plate

(fig. 10) if the surface density of the plate equals . Fig. 10 We find the mass by the formula (3). A domain of integration R is a rectangle with the sides parallel to Ox-, Oy-axes. Using the formula (7) we get

.

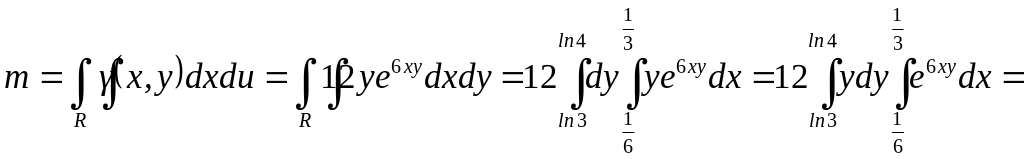
The other order of integration isn’t well (verify!).

Ex. 3. Evaluate by two ways the integral if the domain D is defined by inequalities (fig. 11).

The domain D is that of the first and second types.

The first way. We consider D as a domain of the first type,

, Fig. 11 that is D is bounded

a) from the left by the straight line ;

b) from the right by the straight line ;

c) below by the line ;

d) above by the line .

Using the formula (5) we have

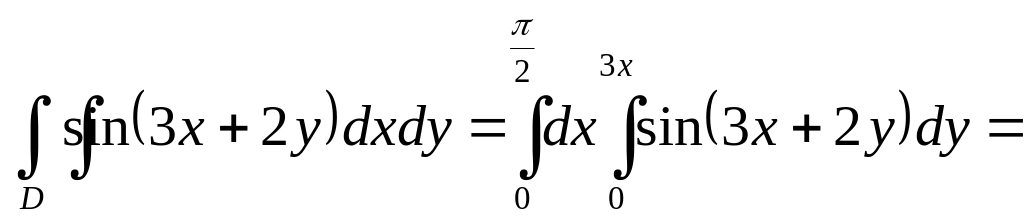
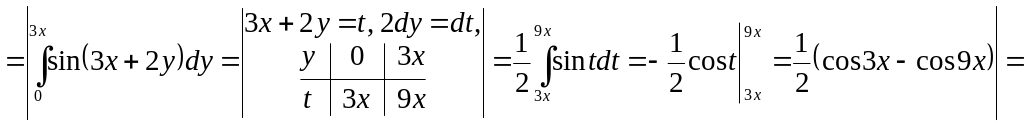
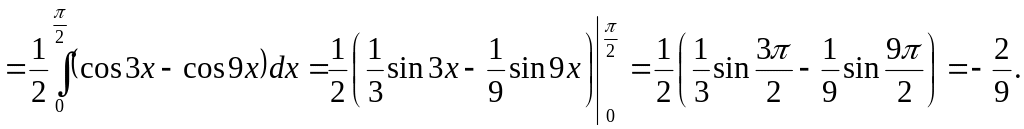
In the second way we treat D as a domain of the second type,

,

that is D is bounded

a) below by the straight line ;

b) above by the straight line ;

c) from the left by the line ;

d) from the right by the line .

Therefore with the help of the formula (6) we write

.

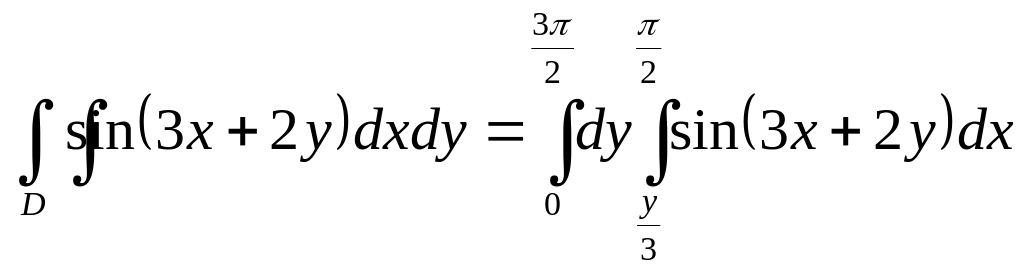Fulfill evaluation of the integral yourselves.

Ex. 4. Set the limits of integration in a double integral over a triangular domain D with the vertices (fig. 12)

At first we compile the equations of the straight lines OA and AB.

OA:

AB:

Fig. 12 .

The first way. The domain D is that of the first type because of it’s bounded from the left by a straight line x = 0, from the right by a straight line x = 5, below by a line , above by a line hence on the base of the formula (5)

.

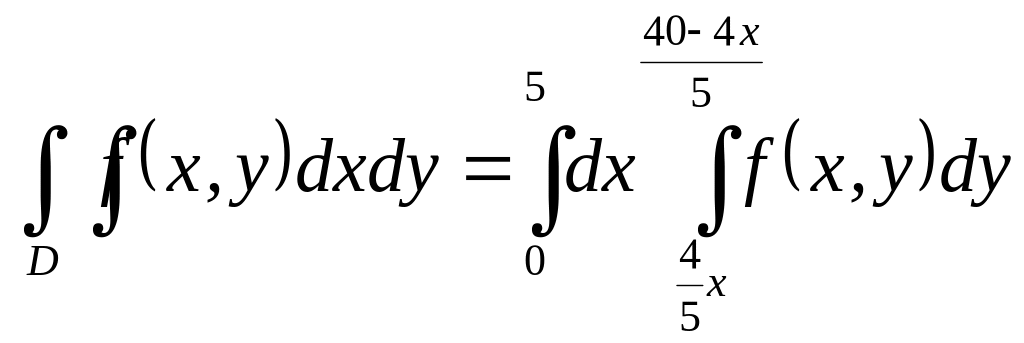The second way. To apply the formula (6) we divide the domain D into two domains of the second type by a straight line y = 4 (fig. 12). If we describe them by two double inequalities, namely

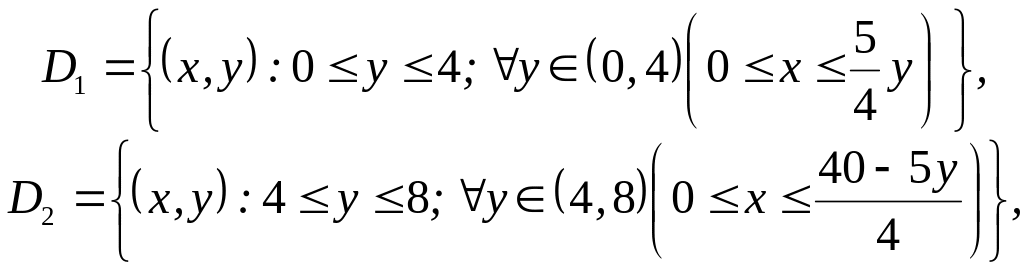
we’ll get

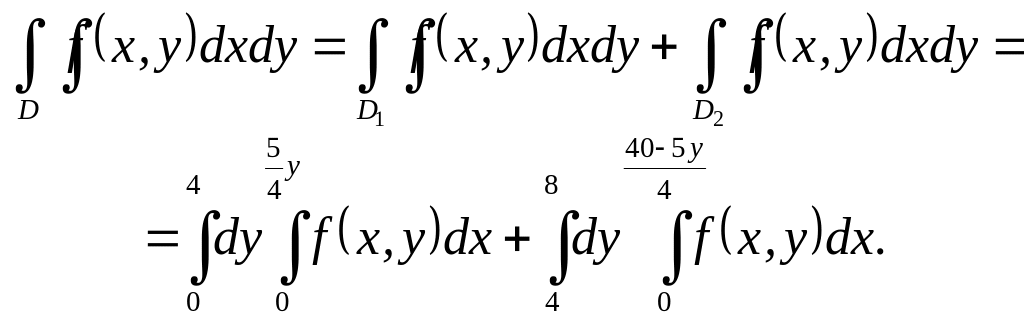
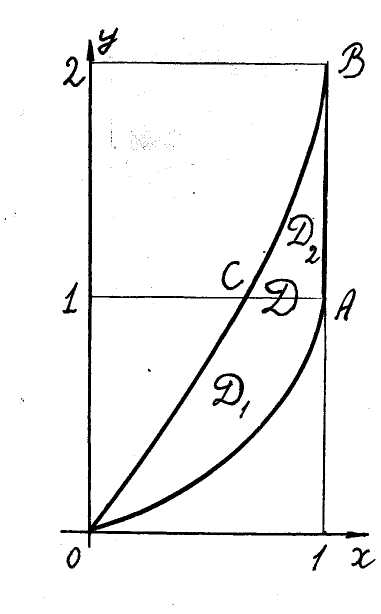
Ex. 5. Evaluate the double integral over the domain

(fig. 13).

The domain D is that of the first type. It can be divided into two do-mains of the second type by the straight line Fig. 13 (fig. 13),

,

,

.

The integral in question equals the sum of two integrals. It’s well to calculate

the first one over the domain D and the second one as the sum of integrals over and .

.
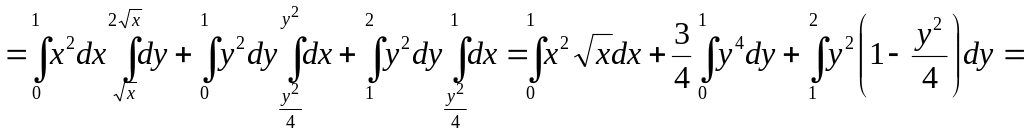