Improper integrals of the second kind
Def 6. Let a
function
is continuous on one of these three sets: a)
b)
,
c)
with discontinuity point a,
b, c
respectively. One introduces the next
three improper integrals of the second
kind (integrals
of discontinuous functions over a finite interval)
namely
;
( 14 )
;
( 15 )
.
( 16 )
Notions of convergence or divergence are introduced in the same way that for improper integrals of the first kind.
Def. 7. The principal value of the integral (16) is called the next limit
.
( 16 )
Ex. 7. Improper integrals
( 17 )
are
convergent for
and divergent for
.
■Let’s study the first integral
.
a) If
we have
(divergence);
b) In the case
■
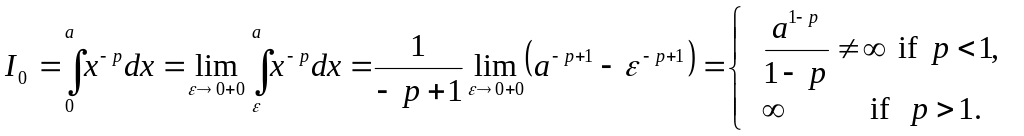Ex. 8. Investigate the integral
for convergence (
is discontinuity point).
.
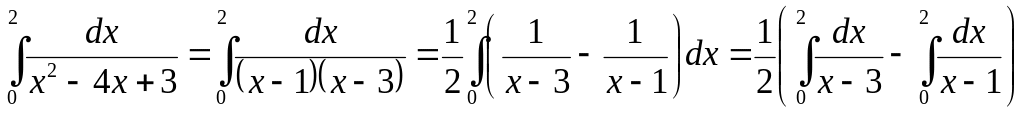The
first integral is usual one because of its integrant is continuous on
the segment
,
and the second is divergent improper integral
.
Therefore the given improper integral diverges.
Ex. 9. Find the principal value of the next
divergent integral
.
.
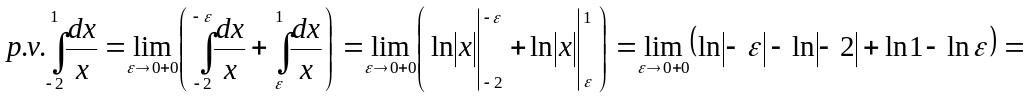
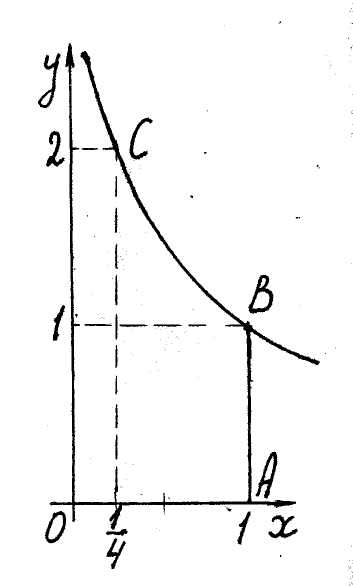Ex.
10. Find the area of an infinite figure bounded by the lines
,
,
,
(fig. 7).
.
Note 2 (Newton-Leibniz formula). Evaluation of improper integrals of the se-cond kind can be represented in the form of
Fig. 7 Newton-Leibniz formula. Let for
example a function
is continuous on an interval
and for any its primitive
we denote
.
Then
Ex. 11.
.
Ex. 12. If
then
,
.
Note 3 (change of a variable and integration by parts in improper integrals). In process of evaluation of improper integrals we can use change of a variable and in-tegration by parts.
Ex.
12. Integrals
of the example 7 can be reduced by change of a variable to the
integral
of the same example. In particular
Ex. 13.
Ex. 14.
Ex. 15. Prove yourselves that
.
Ex.
16. Prove that
.
■
■
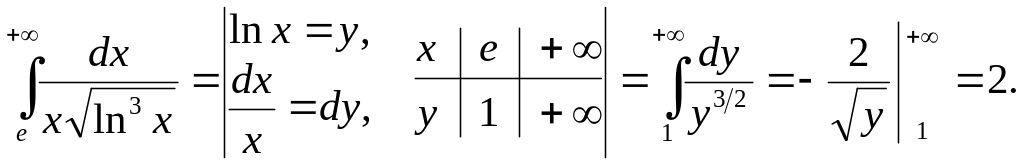Convergence tests
We’ll state and prove theorems for an improper integral
with
an integrand
continuous on the interval
,
but they are valid for all other improper integrals.
Theorem 1. Let
for continuous on
functions
and sufficient large x one
has
.
If the integral
converges then the integral
also converges.
If the integral diverges then the integral also diverges.
■Let for example the integral
converges,
It follows that for any b >
a
and so there exists the limit
,
that is the integral converges.■
Ex. 17. The integral
diverges, because of for any
,
and the integral
diverges.
Ex. 18. Prove convergence of the integral
.
■It’s known that for any
the inequality
holds. Let’s represent the given integral as follows
.
The first and the third improper integrals converge, because of
,
and the integrals
are convergent. Therefore the given integral converges.■
Ex. 19. Prove yourselves divergence of the
integral
.
Ex. 20. Investigate the integral
for convergence.
For any positive x
,
and the given integral diverges on account of divergence of the
integral
.
Theorem 2. Let
for continuous on
functions
and sufficient large x one
has
.
If the integrals
converge then the integral
also converges.
■Validity of the theorem follows from the inequality
and preceding theorem.■
Theorem 3 (absolute convergence). If for continuous on an interval an integral
converges then the integral
converges and is called absolutely convergent.
■Proving follows from the inequality
and the theorem 2.■
Ex. 21. The integral
absolutely converges, for
,
and the integral
converges.
Ex. 22. Prove absolute convergence of the
integrals
,
.