
- •Міністерство освіти і науки україни донецький національний технічний університет
- •Integral calculus (інтеґральне числення)
- •Донецьк 2005
- •Integral calculus lecture no. 19. Primitive and indefinite integral
- •Point 1. Primitive
- •Properties of primitives
- •Point 2. Indefinite integral and its properties
- •Point 3. Integration by substitution (change of variable)
- •Point 4. Integration by parts
- •Lecture no.20. Classes of integrable functions
- •Point 1. Rational functions (rational fractions)
- •Point 2. Trigonometric functions
- •Universal trigonometrical substitution
- •Other substitutions
- •Point 3. Irrational functions
- •Quadratic irrationalities. Trigonometric substitutions
- •Quadratic irrationalities (general case)
- •Indefinite integral: Basic Terminology
- •Lecture no. 21. Definite integral
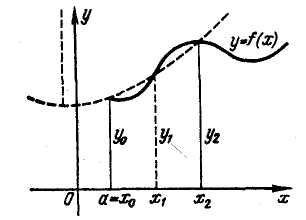
- •Point 1. Problems leading to the concept ofa definite integral
- •Point 2. Definite integral
- •Point 3. Properties of a definite integral
- •I ntegration of inequalities
- •Point 4. Definite integral as a function of its upper variable limit
- •Point 5. Newton-leibniz formula
- •Point 6. Main methods of evaluation a definite integral Change of a variable (substitution method)
- •Integration by parts
- •Lecture no.22. Applications of definite integral
- •Point 1. Problem – solving schemes. Areas
- •Additional remarks about the areas of plane figures
- •Point 3. Volumes
- •Volume of a body with known areas of its parallel cross-sections
- •Volume of a body of rotation
- •Point 4. Economic applications
- •Lecture no. 23. Definite integral: additional questions
- •Point 1. Approximate integration
- •Rectangular Formulas
- •Trapezium Formula
- •Simpson’s formula (parabolic formula)
- •Point 2. Improper integrals
- •Improper integrals of the first kind
- •Improper integrals of the second kind
- •Convergence tests
- •Point 3. Euler г- function
- •Definite integral: Basic Terminology
- •Lecture no. 24. Double integral
- •Point 1. Double integral
- •Point 2. Evaluation of a double integral in cartesian coordinates
- •Point 3. Improper double integrals. Poisson formula
- •Point 4. Double integral in polar coordinates
- •Double integral: Basic Terminology
- •Contents
- •Integral calculus 3
- •Integral calculus (Інтеґральне числення): Методичний посібник по вивченню розділу курсу ”Математичний аналіз” для студентів ДонНту (англійською мовою)
Lecture no. 23. Definite integral: additional questions
POINT 1. APPROXIMATE INTEGRATION
POINT 2. IMPROPER INTEGRALS
POINT 3. EULER Г-FUNCTION
Point 1. Approximate integration
We’ll study the case of nonnegative function
![]() when a definite integral
when a definite integral
![]()
represents the area of a curvilinear trapezium
bounded by straight lines
![]() ,
,
![]() ,
the Ox-axis
and a graph of the function
.
The same results remain valid in general case.
,
the Ox-axis
and a graph of the function
.
The same results remain valid in general case.
Rectangular Formulas
 A. We divide the segment
A. We divide the segment
![]() into n equal
parts of the length
into n equal
parts of the length
![]() by points
by points
![]() .
.
Straight
lines
![]() divide the curve
into n parts
. Let’s denote by
divide the curve
into n parts
. Let’s denote by
Fig. 1
![]()
the
values of the function
![]() at the division points (see fig. 1)
at the division points (see fig. 1)
a) Substituting every part of the curve
by the segments of straight lines
![]() we substitute the curvilinear trapezium by the set of rectangles with
total area
we substitute the curvilinear trapezium by the set of rectangles with
total area
![]()
Therefore
![]()
![]() ( 1 )
( 1 )
b) Similarly, substituting every part of the curve
![]() by the segments of straight lines
by the segments of straight lines
![]() ,
we get
,
we get
![]() ( 2 )
( 2 )
Absolute error of the formulas (1), (2) has the order 1/n, that is

![]() .
.
c) Dividing the segment
![]() into 2n equal
parts of the length
into 2n equal
parts of the length
![]() by points
by points
![]() (fig. 2),
(fig. 2),
we
substitute the curvilinear trapezium by the set of rectan-
Fig.2 gles with bases 2h,
altitudes
![]() and total area
and total area

Hence
![]() ( 3 )
( 3 )
Absolute error of the formula (3) has the order 1/n2, that is
![]()
It means that the formula (3) is more exact than both (1) and (2).
Trapezium Formula

After dividing the segment
![]() into n equal
parts
into n equal
parts
(fig.
3) we divide the graph of the function
into n parts
of the length
![]() by points
by points
![]() .
.
Fig. 3 Substituting every part of
the graph by segments
![]()
we substitute the curvilinear trapezium by the set of trapeziums with total area
![]() .
.
So
we get the next approximate formula (trapezium formula)
![]() ,
,
![]() ( 4 )
( 4 )
Its absolute error has the order 1/n2, that is
![]() .
.
It means that the formulas (3) and (4) have the same order of exactness.
Simpson’s formula (parabolic formula)
Let’s divide (by points
![]() )
the segment
into an even number
2n of
equal parts of the length
and let
)
the segment
into an even number
2n of
equal parts of the length
and let
![]()
be points of the curve corresponding to the division points (see fig. 4 for the case 2n = 6).
At first we draw a quadratic parabola

![]()
through
points
![]() (see
fig. 4, 5). One can prove that the area of the figure between the arc
(see
fig. 4, 5). One can prove that the area of the figure between the arc
![]() of the parabola and the segment
of the parabola and the segment
![]() of the Ox-axis
Fig. 4 equals
of the Ox-axis
Fig. 4 equals
 ,
,
and we can write
 .
.
Fig. 5 Carrying out the same
procedure on the point triplets
![]() …,
…,
![]() we get
we get

![]()
![]()
![]() .
.
Finally we get Simpson’s formula for approximate integration
![]() (5)
(5)
Simpson’s formula (5) is the most exact in comparison with (1) – (4). Indeed, its absolute error has the order 1/n4 that is
![]() .
.
For example in the case n = 3, 2n = 6 (fig. 4) Simpson’s formula has the next form
![]() .
.
Ex. 1. Calculate approximately the integral
![]() .
.
Let’s form the next table of values of the argument and the function:
i |
|
|
|
0 |
|
0.00 |
|
1 |
|
0.04 |
|
2 |
|
0.16 |
|
3 |
|
0.36 |
|
4 |
|
0.64 |
|
5 |
|
1.00 |
|
6 |
|
1.44 |
|
7 |
|
1.96 |
|
8 |
|
2.56 |
|
It
corresponds to division of the segment
![]() into
into
![]() parts of the length
parts of the length
![]() .
.
By the formula (1)
![]() .
.
By the formula (2)
![]() .
.
Using the formula (3) we take 2n
= 8, n =
4,
![]() ,
and so
,
and so
![]() .
.
By the formula (4)
![]() .
.
We’ll apply the formula (5) two times.
At first we divide the segment
into 2n =
4 parts,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
correspondingly
,
correspondingly
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and therefore
,
and therefore

Dividing now the segment
into 2n =
8 parts,
![]() ,
we have
,
we have
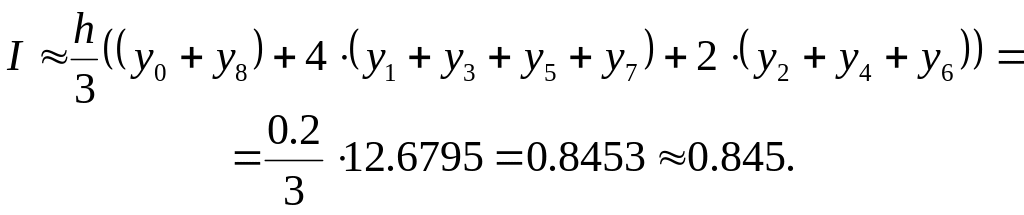
It’s useful to compare all these results with
known approximate value of the same integral up to
![]() ,
namely
,
namely
![]() .
.
