Point 3. Volumes

Volume of a body with known areas of its parallel cross-sections

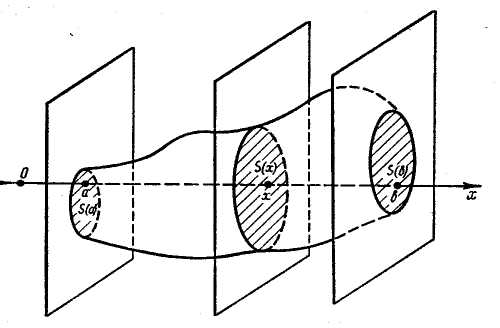
Let some body is situated between the planes , , and for any the area of its cross-se-ction by a plane perpendicular to Ox-axis is known (see fig. 16). The volume of the body equals the integral Fig. 16 . ( 22 )

■ An element of the volume is the volume of a right circular cylinder with the base and the altitude ,

.

Adding all these elements we get the required volume represented by the formula (22).■

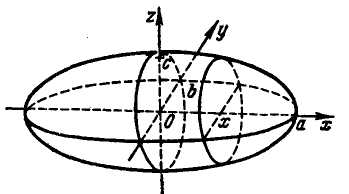
Ex. 15. Find the volume of the triaxial ellipsoid

(fig. 17)

For any the plane section of the body per- Fig. 17 pendicular to the Ox-axis is ellipse with the semi-axes

and the area

.

Therefore the volume of the ellipsoid by the formula (22) equals

.

Volume of a body of rotation

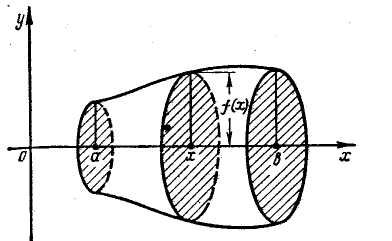A curvilinear trapezium (see fig. 1) rotates about -axis. Prove that the volume of the corresponding body (body of rotation, fig 18) equals the definite integral

. ( 23 )

■ For any a cross-section of the body of ro- Fig. 18 tation by a plane perpendicular to Ox-axis is a circle of radius (fig. 18). Therefore its area , and by the formula (22) the vo-lume of the body in question is given by the formula (23).

Let the same curvilinear trapezium (fig. 1) rotates about -axis and or . Prove that the volume of the corresponding body of rotation is represented by the integral

. ( 24 )

Ex. 16. Let the arc of a sinusoid rotates about the Ox-, Oy-axes. Calculate the volumes of corresponding bodies of rotation.

With the help of the formulas (23), (24) we get

.

.

A curvilinear trapezium (fig. 6) rotates about -axis. Prove that the volume of the corresponding body of rotation is represented by the integral

. ( 25 )

Ex. 17. An ellipse rotates about the Ox-, Oy-axes. Calculate the volumes of corresponding bodies of rotation.

From the equation of the ellipse

,

and by the formulas (24), (25) we have

;

.

Point 4. Economic applications

Problem 1 (produced quantity). Let the labour productivity of a some factory at a time moment t equals . It is known (see the formula (11) of the point 2 of prce-ding lecture) that its produced quantity U during the time interval [0, T] equals

.

Ex. 18. Let the labour productivity of a factory is . Then its produced quantity

.

Problem 2 (costs of conservation of goods). Let is the quantity of goods in the storage at a time moment t, and a quantity h represents the costs of conservation of unit of goods per unit of time. Then the costs of conservation of goods during a time interval (or an element of the costs of conservation) equals

.

Adding all these elements from to we get the costs of conservation of goods during the time interval , that is

.

Let, for example, we study the case of uniform consumption of all goods from at a time to at a time . In this case the quantity of goods at a time mo-ment t is

,

and the costs of conservation of goods equals

.