Point 5. Newton-leibniz formula

Theorem 3. If a function is continuous one on a segment a, b, and F(x) is one of its primitives then Newton-Leibniz formula for evaluation of the definite integral of the function over the segment a, b is true

( 23 )

■ We have two primitives: and the integral (21) with upper variable limit x. By corresponding property of primitives the difference

.

To find the value of the constant C we put . So

,

and therefore

.

Substituting x by b and t by x we obtain the formula (23).■

Note 1. The expression

,

which means the action , is often called the double substitution.

Ex. 5. Calculate the definite integral

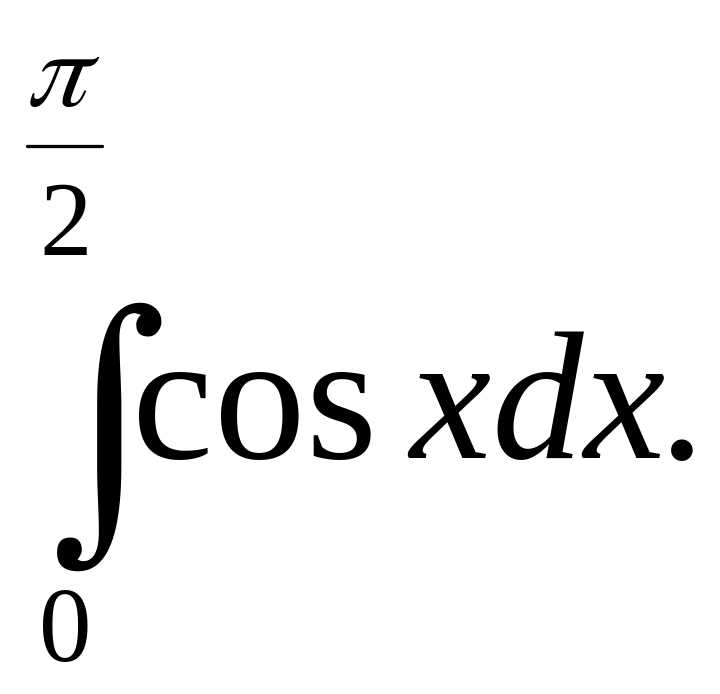
A primitive of is and therefore by Newton-Leibniz formula

Ex. 6. Find the area of a figure bounded by the next lines , (fig. 4).

Fig. 4 The figure in question is a curvilinear trapezium, and so its area by the formula (10) equals the definite integral

.

Ex. 7. A particle moves in a straight line and t sec. after passing a point O the velocity of the particle is ft. per sec. Find the distance of the particle from O after 2 sec.

On the base of the formula (12) the distance in question equals

ft.

Ex. 8. Find the mean value of the function on the segment .

On the base of the formula (20)

.

Point 6. Main methods of evaluation a definite integral Change of a variable (substitution method)

Theorem 4. Let: 1) a function is continuous on a segment [a, b]; 2) a function is continuous with its derivative on a segment [α, β]; 3) φ (α) = a, φ (β) = b. Then the next formula (formula of change of a variable) is true

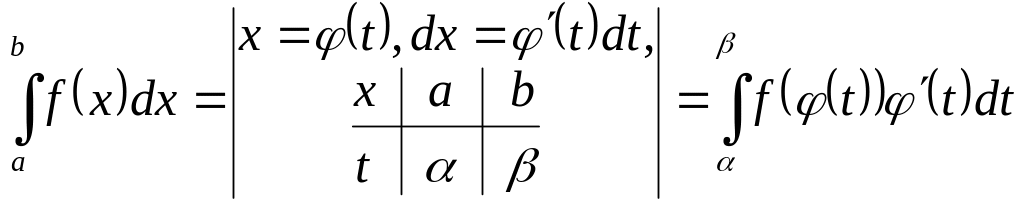. ( 24 )

■ Let is some primitive of a function . Then is the primitive of the function . By Newton-Leibniz formula

;

.■

Note 2. As distinct from an indefinite integral it isn’t necessary to return to preceding variable after integration by the formula (24).

Ex. 9. Calculate the definite integral .

Let’s put . Then , so

Ex. 10. Find the area of a figure bounded by an ellipse (fig. 5).

It’s sufficient to find the quadruplicated area of the Fig. 5 part OAB of the figure.

The first way. From the equation of the ellipse , and so

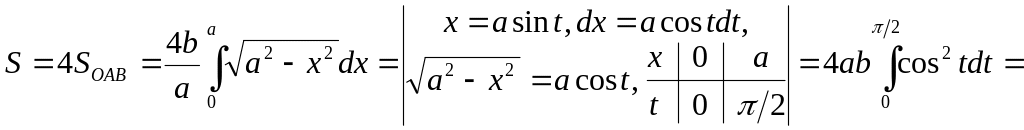
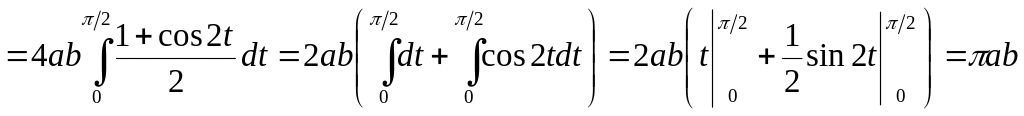
The second way. It’s better to pass to parametric equations of the ellipse, na-mely . In this case

.

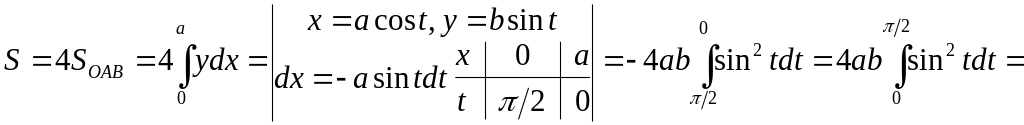
Integration by parts

Theorem 5. If functions are continuous with their derivatives on a segment , then the next formula (formula of integration by parts) is true

( 25 )

■To prove this formula it’s sufficient to integrate from a to b both parts of the identity

and apply Newton-Leibniz formula for the integral of the expression ■

Ex. 11. Evaluate the definite integral .

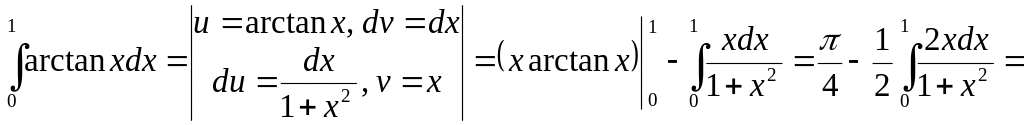
Ex. 12. Find the area of a figure bounded by two curves (see fig. 6).

The curves intersect at the points and form a given figure . Its area is Fig. 6 equal to the difference of the areas of two curvilinear trapeziums . .

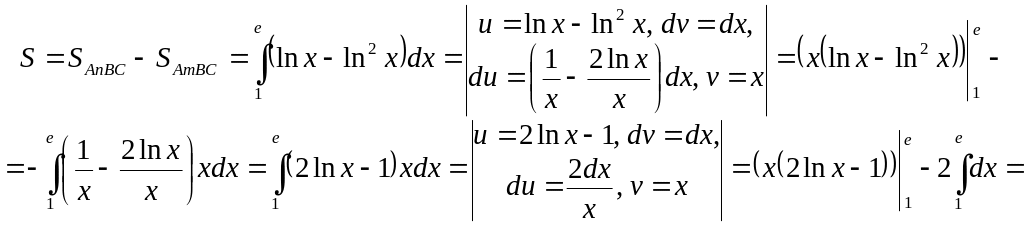
Ex. 13. Let 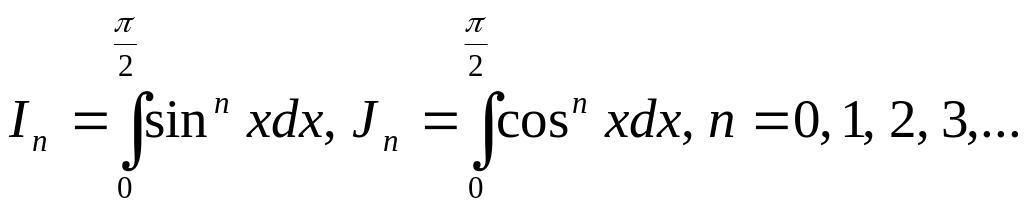. Prove that

.

■

■

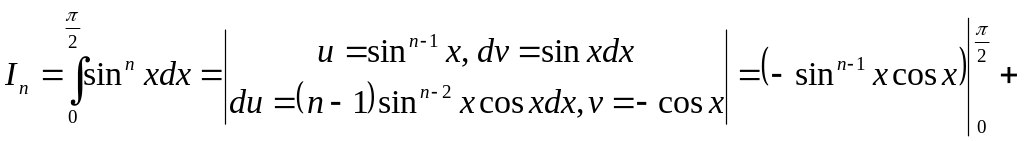
For example

.

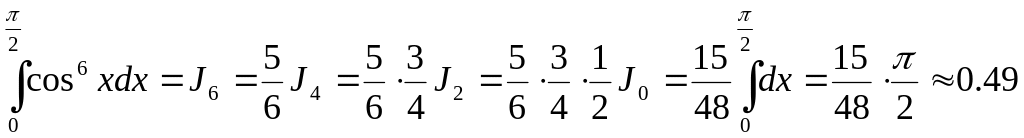Ex. 14. Find the remainder of Taylor formula in Lagrange form.

Let, for example,

.

By Lagrange formula

.

Taking we get

,

and after integration over the segment

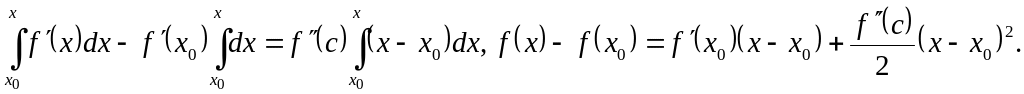Therefore

To get for any n we put and integrate n times over .