41. Розклад ф-ції у ряд Тейлора

Рядом Тейлора функції f (x) називається ряд вигляду:

Тут a – центр розвинення; f ( n )( a ) – значення n -ї похідної в точці x = a ;

– n -й коефіцієнт Тейлора, n = 0 ,1,2 ,....

42.Розклад функції у ряд Фур’є

Ф. f(x) наз. Такою, що відповідає умовам Діріхле на пром.[a;b], якщо вона на цьому пром..:

1)моє скінчене число розривів першого роду

2)має скінчене число екстремумів

3) в усіх точках пром.. [a;b]

Ф f(x), що відповідає умовам Діріхле [-П;П], може бути визначена в усіх точках цього проміжку рядом Фур’є

, де

n=1,2,3….

У випадку парної ф f(x) коеф. для всіх n і ряд Фур’є має вигляд :

, тоді

У випадку непарної ф f(x) коеф. та і ряд Фур’є має вигляд:

, n=1,2,3….

43.Лінії рівня функції кількох змінних. Означення. Навести приклад

Лінією рівня наз. множина всіх точок площини, в яких ф-ія z=f(x;y) набуває однакових значень.

Рівняння ліній рівня записують у вигляді f(x;y)=C.

44.Використання універсальної підстановки при інтегруванні тригонометричних виразів

Інтеграл типу ,де R – раціональна функція своїх аргументів, заміною зводяться до інтегрування функції, яка є раціональною відносно t.

При цьому ; ; ;

На практиці універсальну тригонометричну підстановку використовують,якщо sin x та cos x входять під інтегр. Вираз у невеликому стпені, інакше розрахунки бдуть дуже складні.

45.Метод невизначених коефіцієнтів

Нехай дріб правильний (тобто n<m), а знаменник дробу можна записати у вигляді

, тоді

Де - невизначені коефіцієнти

46.Поняття диференціального рівняння та його розвязоку

Диф. Рівнянням називається рівняння, яке містить шукану похідну ф-ції. Найбільший порядок похідних називається порядком диференційного рівняння.Найб. порядок пох. наз. порядком диф. р-ня.

Звич. ДР наз. нетотож. співвіднош. між шуканою ф-цією однієї змінної самою не залеж. змінною та пох. шук. ф-ції певних порядків.

Розв’язком ДР y’=f(x;y) наз. ф-ція у=(х), яка при підстановці у ДР перетвор. його у тотож.

Розвязок, що містить довільні пост. наз загальним роз. ДР.

47.Теорма Коші про інтегрування та єдиність розв’зку рівняння першого порядку

Інтегральна крива це графік ф., що є розв’язком звичайного піддіференціального рів. Диф. рів. Не розв’язане відносно похідної має вигляд: (1)

Ф розв’язоно відносно похідної: (2)

Задачею Коші для рів. (1)або(2) наз. задачею відшукання функції y=y(x), xє(a,b), яка є розв’язком заданого рів. і задовольняє початкову умову задачі.

(3)

Загал. розв. диф. рів. (1)або(2) це така сукупність функцій , що для будь-якої допустимої фіксованої сталої С ф. є розв’язком даного рів. і для будь-якої допустимої початкової умови(3) існує така С, для якої ця ф. задовольняє дану початкову умову.

Якщо заг. розв. записано у вигляді Ф(x,y,c)=0 , то його наз. загал. інтегралом даного диф. рів.

Якщо ф. f(x,y) має в обл. D неперервні частинні похідні, то через кожну точку цієї обл. проходить єдина інтегральна крива диф.рів y’=f(x,y)

48.Рівняння з відокремленими змінними

Відокремлюваними диф. рів. з відокр. змінними наз.рів. виду

Де всі вказані ф. неперервні на певних проміжках. Такі рів. розв. відокремленням змінних:

; - заг.розв.рів. , або задано у такому вигляді:

49.Однорідні диференціальні рівняння

Д.Р. називається однорідним, якщо його можна подати у вигляді: або

тобто ф. P i Q є однорідними одного й того ж самого порядку.

Ці рів. можна записати у вигляді:

Ці рів. Можна звести до диф.рів. х відокремлюваними зміними за допомогою підстановки

-невідома ф. від х.

50.Лінійні диференціальні рівняння

Лінійним диф.рів. I порядку наз.рів. вигляду -задані неперер. ф. пром.(a;b)

Рів. Розв’язується методом підстановки y=UV, де U та V невідомі ф. тоді

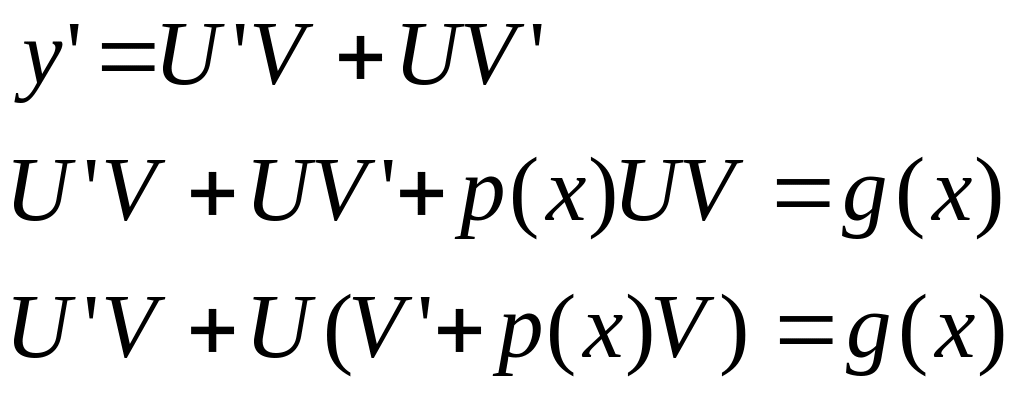
ф. V вибираємо таку, що і тоді

Тоді ф. U визнач. із рів.

51. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами

це рівняння виду ; p і q- числа(коеф.)

f(x)- задана ф.

Розглянемо випадок коли f(x)=0 , то лін. диф. рів. наз. однорідним або без правої частини.

Такі рівняння розв’язують за правилом:

1)скласти характеристичні рів.

розв’язують його та визнач. Корені і

2)якщо і дійсні та різні, то заг. роз. рів. має вигляд

3)якщо = =k є дійсним числом , то заг. роз. рів. має вигляд

4)якщо і спряжені комплексні числа