29.Невласні інтеграли від необмежених функцій (другого роду)

Нехай ф. f(x) визнач. на пром. [a;b), т х=b наз. особливою т. ф. f(x), якщо f(x) при

Нехай ф. f(x) інтегрована на відрізку від [a;b- ] при довільному , такому що , тоді якщо існує скінченна границя то її наз. невласним інтегралом II р. і познач. . Отже за означенням .

У цьому випадку кажуть, що інтеграл існує або збігається, якщо границя нескінчена або не існує то інтеграл також наз. Невласним, але розбіжним.

Анологічно, якщо x=a особлива т., то . Якщо f(x) необмежена в околі якої небудь внутрішньої т. С є (a;b)

30.Наближене обчислення визначених інтегралів

Нехай від заданої та непер. на [a;b] ф-ції у=f(x) треба обч. . Поділимо [a;b] т. а=х₀, х₁, х₂,…,х_n-1, x_n=b ф-ції на n рівних частин завдовжки . Знач. ф-ції f(x) у т. х_і, і=(0,n) познач. так: у₀=f(x₀), у₁₌ f(x₁),…, у_n=f(x_n)

Формула трапецій

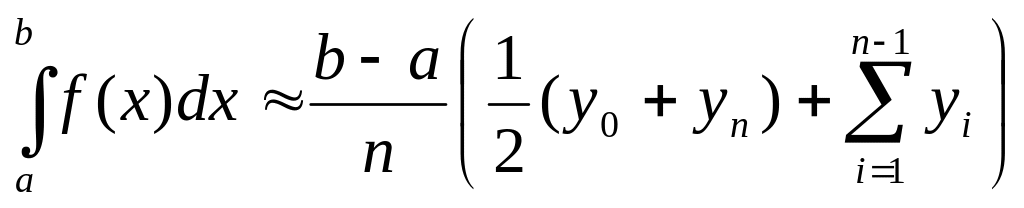Формула Сімпсона

31.Означення числового ряду. Сума числового ряду

Рядом наз. вираз (1), тобто сума з нескінченою кіл-стю доданків кожний доданок ряду (1) наз. його челоном.

Якщо всі члени ряду (1) задані числами то цей рчд наз. числовим.

Приклад числових рядів:

1)геометричний де , q- задані числа

2)гармонічний

3)узагальнений гармонічний , а- задане число.

Суму наз. n-ою частковою сумою числового р.(1), а границю наз. Сумою всіх

32.Властивості рядів. Збіжність числового ряду

Теорема: Якщо ряд збіжний, то:

Властивості рядів:

1)числовий ряд (1) збігається т.і т.т. , коли (критерій Коші)

2)якщо р.(1) збігається , то загал. член , це необхідна умова збіжності ряду.

3)р. (1) збігається т.і т.т. , коли збігається його n-ий залишок

4)для двох збіжних рядів і чисел , тобто збіжні. можна почлено додаватиЮ а спільний множник можна виносити за знак суми.

5)у збіжному ряді ожна довільно будувати(брати у дужки,не переставляючи местами на збіжність та на його суму це не впливає ).

33.Умови збіжності додатних рядів

Означення: знакододатний ряд – ряд вигляду U₁+U₂+…+U_n+…, всі члени якого є додатними(невідємними)

Додатній ряд є збіжним (розбіжним) якщо:

1) Ознака порівняння рядів.

Існує збіжний(розбіжний)додат.р. для якого (перша ознака порівняння)

або (друга ознака порівняння)

2) Ознака Даламбера:

Якщо для знакододатного ряду

існує

то, якщо:D>1, ряд – розбіжний; D<1, ряд – збіжний

3) Радикальна ознака Коші.

k<1, ряд – збіжний; k>1, ряд – розбіжний

4) Інтегральна ознака Коші.

Беремо  від -члена ряду. Якщо невласний інтеграл збіжний, то ряд – збіжний, якщо ж розбіжний, то ряд – розбіжний.

34. Знакозмінні ряди. Ознака Лейбніца.

Знакозмінні ряди це ряди вигляду :

Ознака Лейбніца:

Знакозмінний ряд є збіжним, коли

1)

2)

35.Абсолютно та умовно збіжні ряди

Числовий ряд (1) із довільними членами наз. Абсолютно збіжним, якщо збігається ряд , кожний абсолютно збіжний ряд є також збіжним, але не навпаки.

Р. (1) наз. умовно збіжним,якщо він є збіжним , проте не абсолютно. В абсолютно збіжних рядах можна переставляти місцями члени, що не впливає на його суму. Абсолютно збіжні ряди можна перемножати за правилом Коші. , де