
- •Понятие вариации. Основные показатели вариации
- •Абсолютные показатели вариации
- •Относительные показатели вариации
- •Свойства дисперсии:
- •Вариация качественных признаков
- •Понятие выборочного наблюдения
- •2.Способы и виды отбора ед.-ц из генеральной сов.-ти.
- •3.Ошибки выборочного наблюдения
- •4 .Определение численности выборки
- •5.Малая выборка, её особенности и границы применения
- •1.Понятие о рядах динамики. Виды рядов динамики, правила их построения. Сопоставимость данных в динамики.
- •2.Аналитические показатели ряда динамики
- •3.Методы выявления основной тенденции развития
- •1.Виды и формы взаимосвязей, изучаемых в статистике
- •Статистические методы изучения связей: метод параллельных рядов, метод аналитических группировок, графический метод, балансовый метод, регрессионный анализ
- •3.Корреляционный анализ тесноты связи соц.-эк. Явлений: расчёт коэф.-та и индекса корреляции, эмпирического корреляционного отношения и коэф.-та детерминации.
- •1.Индексы, их сущность и классификация. Индивидуальные и общие индексы.
- •2.Агрегатный индекс - основная форма общего индекса. Сопряжённые индексы
- •3.Средние индексы: средний арифметический и гармонический индексы
- •4.Ряды индексов с постоянными и переменными весами
- •5. Индексы динамики среднего уровня. Система взаимосвязанных индексов
- •6. Индексы рынка ценных бумаг
- •7.Индексы потребительских цен на товары и услуги.(ипц)
Тема: «Статистическое изучение вариации»
Понятие вариации. Основные показатели вариации
Средняя величина – абстрактная обобщ. хар.-ка признака изучаемой совокупности. Однако она не хар.-ет строение этой сов.-ти, не показывает колебания изучаемого признака. В тех случаях, когда отдельные значения признака близки к ср. величине, она явл.-ся типичной(репрезентативной). Если отдельное значение признака у различн. единиц сов.-ти далеки от значения средней, она явл.-ся нетипичной и плохо представляет совокупность.
Средние хар.-ки необходимо дополнить показателями, кот. измеряют отклонения индивид. значений признака от ср. величины. К таким показателям относятся:
1)Абсолютные показатели вариации:
Размах вариации(R)
Среднее линейное отклонение(¯d)
Дисперсия (
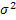 )
)Среднее квадратное отклонение (
 )
)
2)Относительные показатели вариации:
Асциляции (КR)
Лин. коэф.-т вариации (Кd)
Общий коэф.-т вариации (К (V))
Абсолютные показатели вариации
Размах вариации – разность м/у мах и мin значением варьирующего признака, т.е. этот показатель показывает в каких пределах колеблется значения изучаемого признака.
R=Xmax - Xmin
Среднее лин. отклонение – средняя величина из абсолютных отклонений индивид. значений признака от средней величины.
![]() =
=![]() ,
х – отклонения
,
х – отклонения
![]() =
=
![]() - для дискретного ряда
- для дискретного ряда
Дисперсия – ср. квадрат отклонений индивид. значений признака от их средней.
![]() 2
=
2
= ![]()
2
= ![]()
Формула для расчёта дисперсии м.б. преобразована:
2
= ![]()
Дисперсия имеет большое значение в стат. анализе, однако её применение не всегда удобна, т.к. она безразмерная величина. Для измерения вариации признака выч.-ют среднее квадр. отклонение. Она показывает как расположена осн. масса единиц сов.-ти около средней арифметич.:
![]() =
= ![]()
![]() =
= ![]()
Относительные показатели вариации
Относительные показатели рассчит.-ся как отношение абсолютных показателей вариации к к средней арифметической. Чаще всего они выр.-ся в %.
КR
= ![]() ·100
·100
K¯d
=![]() .100
.100
K
= ![]() .100
.100
По величине коэф.-та вариации судят по степени вариации изучаемого признака. Чем больше его величина, тем больше разброс значений около средней. Следовательно тем менее однородна сов.-ть и менее представительна средняя. Сов.-ть счит.-ся однородной, если этот коэф.-т не превашает 33%. Коэ.-т вариации явл.-ся единственно возможными показателями вариации в тех случаях, когда необходимы стат. сов.-ти с разными единицами сов.-ти.
Свойства дисперсии:
1.Если все значения признака уменьшить или увеличить на какое-то число, то дисперсия не изменится.
2.Если все значения
признака уменьшить или увеличить в а
раз, то
дисперсия соотв.-но уменьшится или
увеличится в ![]() раз.
раз.
3.Если все частоты сократить или увеличить в како-то число раз – дисперсия не изменится.
Если исп.-ть все 3 св.-ва одновременно , дисперсия рассчитывается способом момента или способом отсчёта от условного 0.
2 =
= ![]() =
=

Вариация качественных признаков
Для того, чтобы измерить вариацию альтернативного признака введём обозначения:
1-наличия изуч.-го признака
0-отсутствие изуч.-го прзнака
p-та часть единиц, кот.обладает изуч.-ым признаком
q-та часть единиц, кот. не обладает изуч.-ым признаком
Ощая численность совокуп-ти будет p+q=1
2 =
![]() =
=
![]()
x |
f |
xf |
1 |
P |
1p |
0 |
q |
0p |
=
![]()
Вывод: Ср. величина для стат. сов.-ти , в кот. индивид. значение признака принимают 1 из 2 возможных значений равны доли тех единиц,кот. обладают изучаемым признаком.
![]()
Тема: «Выборочный метод в статистике»
