9

ЗАДАНИЕ К РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЕ ПО КУРСУ

«АВТОМАТИЗАЦИЯ СРЕДСТВ МЕХАНИЗАЦИИ И РОБОТОТЕХНИКА»

для студентов специальности 1-53 01 01-05 «АТПП»

СОДЕРЖАНИЕ

1 РАСЧЕТ ПАРАМЕТРОВ ГИДРОПРИВОДА СТАЛКИВАТЕЛЯ ГРУЗА С КОНВЕЙЕРНОЙ ЛЕНТЫ 4

2 РАСЧЕТ РАЗРЕШАЮЩЕЙ СПОСОБНОСТИ, ТОЧНОСТИ РОБОТА И ПРОЦЕНТА СТОЛКНОВЕНИЙ СХВАТА РОБОТА С ДЕТАЛЯМИ 4

3 ПОСТРОЕНИЕ РАБОЧЕЙ ОБЛАСТИ УНИВЕРСАЛЬНОГО ПРОМЫШЛЕННОГО РОБОТА 8

Оценка за РГР и срок выполнения.

РГР, выполненные индивидуально (по последнему номеру зачетки), без явного списывания (или без «следов» группового выполнения) будут оцениваться от 100 баллов, остальные (с одинаковыми рисунками, формулами, пояснениями и т.д.) – от 75.

Срок сдачи: 21.05.2012. Сдавшим 22-25.05.2012 г. оценка снижается на 10%. Сдавшим после 25 мая оценка будет снижена на 20%.

1Расчет параметров гидропривода сталкивателя груза с конвейерной ленты

Пользуясь данными табл. 1, определить параметры гидропривода сталкивателя груза (в виде коробки) с горизонтальной конвейерной ленты: минимальное давление рабочей жидкости P, внутренний диаметр гидроцилиндра D, рабочий ход штока L. Необходимо учесть: силу трения груза о ленту, массу штока и поршня. Недостающие параметры выбрать и рассчитать самостоятельно: материал штока и поршня, диаметр штока и ширину поршня и др. Конструкцию всех элементов выбрать самостоятельно. Нарисовать в примерном масштабе с указанием размеров схему данной технологической операции (конвейерная лента, груз, сталкиватель, приемное устройство для груза и др.).

Таблица 1 – Данные для расчета

№ варианта Пара- метры
Ширина конвейерной ленты, S, мм	400	450	500	550	600	400	450	500	550	600
Масса груза, m, кг	10	15	20	25	30	35	40	45	50	55
Коэффициент трения груза о ленту, f1	0,1	0,11	0,12	0,13	0,14	0,15	0,16	0,17	0,18	0,19
Коэффициент трения штока и поршня внутри цилиндра, f2	0,01	0,02	0,03	0,01	0,02	0,03	0,01	0,02	0,03	0,01

2Расчет разрешающей способности, точности робота и процента столкновений схвата робота с деталями

Пользуясь данными табл. 2, определить разрешающую способность, пространственную разрешающую способность, точность звена робота, процент столкновений схвата робота с деталями.

Теория.

Разрешающая способность - это наименьшее смещение схвата, осуществляемое системой управления роботом при данной разрядности АЦП и ЦАП в цепях обратной связи и управления. Например, если схват робота перемещается на максимальное расстояние d при использовании n-разрядных кодов ЦАП и АЦП в системе управления и приводах, то наименьшее линейное перемещение составляет d/ 2ⁿ. Это происходит из-за того, что отрезку d ставится в соответствие 2ⁿ кодов.

Для вращательных движений нужно делить угловой диапазон  на 2ⁿ, чтобы определить угловую разрешающую способность управления, а затем умножить ее на длину исполнительного механизма для вычисления разрешающей способности на схвате.

Пример 1. Найти разрешающую способность управления линейно перемещающимся схватом, если он проходит расстояние 1000 мм при использовании 10-разрядных кодов ЦАП и АЦП в цепях обратной связи и управления (рис. 1, а). Решение. Имеется 2¹⁰=1024 точек дискретизации на отрезке 1000мм. Таким образом, разрешающая способность управления равна CR=1000/1024=0,9766 мм.

Таблица 2 – Данные для расчета

№ варианта Пара- метры
Движение	Поступ.	Вращ.	Поступ.	Вращ.	Поступ.	Вращ.	Поступ.	Вращ.	Поступ.	Вращ.
Угол поворота, , град		210		230		250		270		290
Длина звена робота, мм		900		1000		1100		1300		1500
Перемещение х, мм	1000		1100		1200		1300		1400
Разрядность АЦП и ЦАП	6	8	10	12	16	6	8	10	12	16
Механическая ошибка робота, мм	0,01	0,015	0,02	0,025	0,03	0,01	0,015	0,02	0,025	0,03
Разрешающая способность, мм
Пространственная разрешающая способность, мм
Точность робота, мм
Размер захватываемой детали с допуском, мм	250,01	270,02	280,03	290,03	300,04	250,03	270,01	280,02	290,04	300,05
Ожидаемое положение схвата робота	25,1	27,1	28,1	29,1	30,1	25,2	27,2	28,2	29,2	30,2
Процент столкнов. схвата робота с деталями, %

Пример 2. Найти разрешающую способность управления робота, работающего в полярной системе координат, при радиусе руки 700 мм и угловом диапазоне вращения 270 , если в приводе используются 8-разрядные коды ЦАП и АЦП в цепях обратной связи по положению и управления (рис. 1, б).

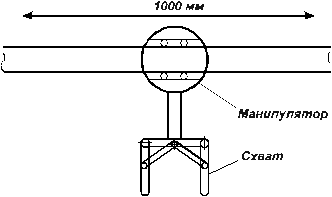
Рисунок 1

а) манипулятор с призматическим сочленением

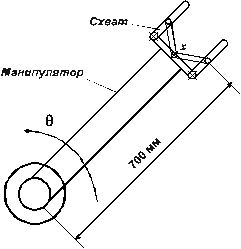
б) манипулятор, работающий в полярной системе координат

Решение. Угловая разрешающая способность управления определяется по формуле

 =(270/180)/256=0,01841 рад.

Тогда разрешающая способность управления на схвате равна

R=7000,01841=12,887 мм.

Заметим, что, если бы использовалось поступательное сочленение, разрешающая способность управления составила бы

CR=700/256=2,743 мм,

что свидетельствует о том, что разрешение при поступательном перемещении в данном случае выше, чем разрешение при вращении.

Пример 3. Определить разрешающую способность управления и ошибку робота модели PUMA, показанного на рис. 2. Определить также пространственную разрешающую способность и точность робота, если механическая ошибка равна 0,02 мм. (Предполагается, что для обратной связи по положению и для управления используется 10-разрядный ЦАП.) Рассматривать только плоскую задачу.

Решение. Для сочленения А:

Угловое разрешение UR=200·2 /(360·1024)=0,0034 рад.

Разрешающая способность управления в точке В по отношению к сочленению А равна 0,0034·425=1,445 мм.

Для шарнира В:

Угловое разрешение UR=270· /(180·1024)=0,0046 рад.

Разрешающая способность управления в точке С по отношению к сочленению В равна 0,0046·425=1,955 мм.

Точности сочленений равны соответственно 0,7225 мм и 0,9775 мм. Окончательно пространственные точности сочленений равны 0,7325 и 0,9875 мм соответственно.

Рисунок 2 – Строение робота PUMA 560

Разрешающая способность управления, а также пространственная разрешающая способность и ошибки робота имеют статистическое распределение. Примем, что эти распределения являются гауссовыми (нормальными), такими, что существуют среднее и среднее квадратическое отклонения ошибок. Для данной целевой точки позиционирования пространственные ошибки могут рассматриваться как допуски на размеры захватываемой детали. Среднее квадратическое отклонение при нормальном распределении может быть определено как 1/3 этих допусков. При помощи следующей процедуры можно найти процент деталей, с которыми произойдет столкновение.

Находится математическое ожидание положения робота _r, соответствующее целевой точке. Пространственные ошибки интерпретируются как допуски t_r; таким образом, _r±t_r - ожидаемое положение схвата робота. Математическое ожидание размера захватываемых деталей обозначим через _p с двусторонним допуском t_p. Средние квадратические отклонения для схвата робота и детали _r и _p могут быть вычислены как

_r = t_r /3 и _p = t_p /3. (1)

Из формулы (2) можно найти значение Z, соответствующее желаемой площади под кривой нормального распределения; оно равно

. (2)

По значению Z находим соответствующую A_Z в табл 3. Вероятность столкновения или процент отсева могут быть найдены из соотношения P=0,5-A_Z. Если для сборки узла используется более двух деталей, применяем ту же процедуру для нахождения средних размеров всех деталей, которые необходимо вводить внутрь других деталей. Находим соответствующие средние квадратические отклонения и переходим, как показано выше, к определению Z, а затем процента отсева, обусловленного столкновениями. Последующий пример поясняет положение.

Пример 4. Манипуляционный робот вводит круглый вал в отверстие, причем d_s=24,99±0,005 мм и d_h=25±0,01 мм. Суммарная пространственная ошибка разрешения (точность) на схвате робота равна 0,005 мм. Определить процент отсева, обусловленного столкновениями, в предположении нормального закона распределения отклонений.

Решение. Эффективный диаметр вала при учете ошибок позиционирования робота равен

d_s*=24,9925±0,0075 мм.

Средние квадратические отклонения вала и отверстия равны соответственно

_s*=0,0075/3=0,0025, _h=0,01/3=0,0033,

так что (_s*²+_h²)^1/2=0,00414. Окончательно Z=(25-24,9925) /0,00414=1,81.

Это соответствует (см. табл. 1) A_Z=0,4649. Тогда P=0,5-0,4649=0,0351 или процент отсева равен 3,51%.