Недетерминированные конечные автоматы.

Пусть A⁰– недетерминированный конечный автомат.

A⁰= <P⁰,S⁰,s₀⁰,φ⁰,F⁰>

F⁰– множество конечных подмножеств алфавита состояний.

S = {S₀ , S₁ , S₂}

M(S) = {{ S₀ } , { S₁ } , { S₂ } , { S₀ , S₁} , { S₀ , S₂} , { S₁ , S₂} , { S₀ , S_{1 ,} S₂}}

M^* <= M

φ:P*SS– детерминированный алфавит

φ⁰:P*SM^*- недетерминированный автомат

Отличие недетерминированного автомата состоит в том, что функции перехода может определять не одно состояние, в которое переходит автомат, а некоторое подмножество состояний.

ТЕОРЕМА:ЕслиL(A⁰) – язык который допускается некоторым конечным автоматомA⁰, то существует детерминированный конечный автоматAкоторый допускает этот же язык.

Преобразование недетерминированного автомата в детерминированный.

Имеется два способа:

1. Общий способ

Пример:

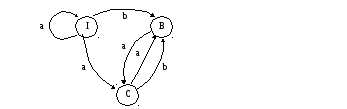
P = {a,b}

S = {I,B,C}

M(S) = {[I] , [B] , [C] , [IB] , [IC] , [BC] , [IBC] , o}

φ( I , a) = [I , c]

φ( I , b) = [B]

φ( B , a) = [C]

φ( B , b) = []

φ( C , a) = [B]

φ( C , b) = [B]

φ( IB , a) = [IC]

φ( IB , b) = [B]

φ( IC , a) = [I ,C , B]

φ( IC , b) = [B]

φ( BC , a) = [BC]

φ( BC , b) = [B]

φ( IBC , a) = [IBC]

φ( IBC , b) = [B]

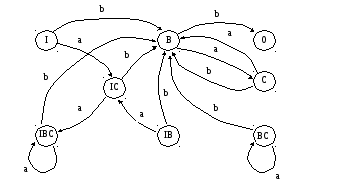
Вершины IBиBCявляются недостижимыми, а вершины 0 нет в выходном сигнале для состоянияB, следовательно граф упроститься:

Это общий способ построения автомата.

Недостаток заключается в том, сто в процессе преобразования возникает большое число недостижимых вершин, которые необходимо удалять.

2 способ. Сокращенный способ.

1. Строится заготовка таблицы переходов детерминированного конечного автомата.

2. В качестве начального состояния выбирается начальное состояние недетерминированного автомата и для него строим подмножество состояний, в которое переходим из начального. Строку заносим в заготовку таблицы переходов.

3. Если полученное подмножество состояний или состояния отсутствуют в левой части таблицы переходов, то они заносятся туда и осуществляется переход к пункту 2.

Процесс заканчивается если в результате получения подмножества, мы не получаем новое подмножество , которое создается в левом столбце.

Пример:

Pi / Si	a	b
I	IC	B
IC	ICB	B
B	C	---
ICB	ICB	B
C	B	B

Пример :Недетерминированный конечный автомат.

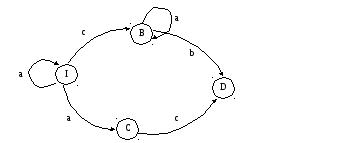
D– конечная вершина.

Преобразование некоторых типов грамматики к автоматному ввиду.

Утверждение : любой конечный язык, не содержащий пустой цепочки является автоматным языком, следовательно существует автоматная грамматика, порождающая данный язык.

Доказательство данного утверждения заключается в указании способа построения автоматной грамматики, порождающий данный язык.

Пусть задан язык:

L= {x₁x₂x₃…x_n}x_i€V_t^*

X_i = a₁a₂a₃…a_m a_i €V_t

Для построения грамматики введем следующие нетерминальные символы: A₁A₂…A_m-1и следующие правила:

X_i  a₁A₁ A₁ a₂A₂ …A_m-2a_m-1A_m-1 A_m-1a_m

Применяя данную процедуру по всем цепочкам X_iполучим множество порождающих правил автоматной грамматики, соответствующей исходному языку.

Рассмотрим контекстно-свободные грамматики.

Контекстно-свободная грамматика является левосторонней , если все ее правила только левосторонние (правосторонняя наоборот) либо заклячительные правила.

Правила вида:

AxB– правосторонняя, гдеA,B– нетерминальные символы.

ABx– левосторонняя.

Ax– заключительное правило.

Для любой правосторонней или левосторонней грамматики может быть построено эквивалентная ей правосторонняя или левосторонняя автоматная грамматика.

Доказательство:

G= <V_t,Vⁿ,I,R> создается набор правил вида:

A  xB, гдеx € V_t^*

Предположим, что x_i=a₁a₂…a_mвведем нетерминальные символыA₁A2…A_m-1и добавим правилоAa₁A₁

A₁a₂A₂ A_m-1 a_m-1A_m-1 A_m-1  a_mB либо A_m-1  a_m

Цепочка правил, заканчивающаяся A_m-1 a_mBзаменит одно правилоAxB. Цепочка правил, заканчивающаясяA_m-1 a_mзаменит правилоAx

Применяя данную процедуру по всем контекстно-свободным грамматикам получим набор правил автоматной грамматики. В любой контекстно-свободной грамматики могут оказаться правила вида AB, она может быть преобразована к контекстно-свободную грамматику не содержащую таких правил.

если ώξ₁Aξ₂ и есть правило

AB,BCxто применяя эти правила в результате получим:

ξ₁Aξ₂ξ₁Bξ₂ ξ₁Cxξ₂это равносильно тому, чтоACx

Доказательство: пусть есть правило вида

R={…AB…BCx}

В этом случае вывод любой цепочки, содержащий нетерминальный символ A, осуществляется следующим образом, пусть есть вывод

ώξ₁Aξ₂, тогда данная цепочка преобразуется в конечную следующим образом:

ξ₁Aξ₂ ξ₁Bξ₂ ξ₁Cxξ₂

Равносильно A  Cx

Чтобы исключить цепочку ξ₁Bξ₂вместоA,Bнужно записатьACx.