6.3. Приклад. Побудувати мп-автомат, який розпізнає мову

{шш^Е | ш Є {а,Ь}*}.

Цей приклад аналогічний до попереднього за винятком того, що вхідне слово не містить всередині букви с і, отже, ми не знаємо, коли починати порівняння між буквами вхідного слова і буквами стеку. Як же вирішити цю проблему? Нагадаємо, що МП-автомат є НСА, а тому ми можемо в будь-який час починати порівняння. Вхідне слово аналізується доти, доки вхідні букви, що залишилися, зіставляються коректно з буквами стеку по відношенню до деякої точки поділу. Звідси слідує, що шуканий МП-автомат задається графом:

Ь, е/Ь а, е/а

Ь, Ь/е а, а/е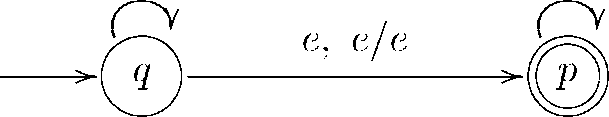

Побудуємо три обчислювальні шляхи для слова аЬЬа, перший з яких розпізнає дане слово, а два інші - ні.

(Д, аЬЬа, е) ь (д, ьЬа, а) ь (д, Ьа, Ьа) ь (р, Ьа, Ьа) ь (р, а, а) ь (р, е, е); (д, аЬЬа, е) ь (д, ьЬа, а) ь (д, Ьа, Ьа) ь (д, а, ьЬа) ь (р, а, ьЬа);

(д, аЬЬа, е) \ (д, ЬЬа, а) \ (д, ЬЬа, а).

6.4. Приклад. Побудувати МП-автомат, який розпізнає мову

{0^П1^П | п = 0,1,...}.

Користуючись тим же методом, що і в прикладі 6.3, побудуємо граф шуканого автомата.

0, е/0 МЯ.

1, 0/е

О

мСр

е, е/е

При роботі даний автомат зчитує у пам'ять першу половину вхі­дного слова, що складається з нулів, а потім видаляє з пам'яті по одному нулю на кожну одиницю, що поступає на вхід. Крім того, переходи станів гарантують, що всі нулі передують одиницям.

З прикладів 5.7 і 6.4 випливає, що клас мов, які розпізнаються МП-автоматами, ширший від класу регулярних мов. Дані мови на­зиваються контекстно-вільними.

6.5. Приклад. Побудувати МП-автомат, який розпізнає мову

{а^іЬс^к | і, к > 0, і + к = і}.

Основна ідея для розв'язання цієї задачі полягає у використанні різних станів для того, щоб зберігати правильний порядок входжень букв а, Ь і с, а також у використанні стеку для дотримання виконання рівності і + к = і. Таким чином, побудуємо МП-автомат з трьома станами з, д і р, де 5 - початковий стан, р - єдиний кінцевий стан. В стані з автомат кожну букву а відправляє у стек. В стані д він аналізує букви Ь вхідного слова і, або порівнює букви Ь з буквами а зі стеку, або відправляє букви Ь у стек. В стані р він аналізує букви с і співставляє їх з буквами Ь зі стеку.

Ь, е/Ь Ь, а/е

а, е/а

г>

с, Ь/е

СУ

е, е/е

е/е

6.6. Приклад. Побудувати МП-автомат, який розпізнає мову {а^гЬ | 2і =

Для того, щоб слово належало шуканій мові, мають виконуватись рівності і = 3к та і = 2к для деякого к > 0. Таким чином, для кожної букви а вхідного слова потрібно занести дві копії букви а в стек. Далі, кожну букву Ь вхідного слова треба співставити з трьома буквами а стеку. Як же занести дві букви а у стек? Ми можемо занести одну букву а у стек, а потім перейти в допоміжний стан для занесення другої букви а у стек. Аналогічно, спершу порівнюємо кожну букву Ь вхідного слова з однією буквою а, а потім переходимо в два інші допоміжні стани для видалення двох зайвих букв а зі стеку. Граф МП-автомата має вигляд:

Вправи до лекції 6.

6.1. Знайти мову, яка розпізнається МП-автоматом, заданим гра­фом:

0, е/0

О

1, 0/е

СУ

е, е/е

>

6.2. Побудувати МП-автомат, який розпізнає мову:

а) {0^П 1^т2^П | п, т — 0};

б) {аЬ^с^к | і, к — 0, і + і = к};

в) {аЬ^с^к | і, і, к — 0, і = ^ + к};

г) {аVс^к | і, і, к — 0, і + 2к = і};

д) {0^п 1^3п | п, т — 0};

е) {0^п 1^т | п, т — 0, 2п = 5т}.

Розділ III

Формальні алгоритмічні моделі Лекція 1. Машина Тюрінґа. Аналіз МТ.

В попередньому розділі ми вивчили два типи обчислювальних моделей: скінченні автомати і автомати з магазинною пам'яттю, які розпізнають регулярні та контекстно-вільні мови відповідно. Зро­зуміло, що дані моделі мають обмежені обчислювальні можливості в порівнянні з реальними персональними компютерами. Наприклад, формальна мова {а^пЬ^пс^п | п — 0} не розпізнається жодним із зга­даних вище скінченних автоматів, але може бути легко обчислена з допомогою короткої програми на ПК.

В цьому розділі ми опишемо нову обчислювальну алгоритмічну модель, яка називається машиною Тюрінґа (МТ). Основні відмін­ності між машиною Тюрінґа та скінченним автоматом полягають в тому, що стрічка МТ нескінченна і МТ може пересуватись по стрі­чці (чи зміщувати стрічку) в будь-якому напрямі. Це надає машині потенційно нескінченну пам'ять, яку можна використовувати під час обчислень.

МТ складається з керуючого присторою, що міститить головку і зовнішньої пам'яті (стрічки), розмір якої потенційно необмежений. Головка машини Тюрінґа може рухатися вздовж стрічки праворуч і ліворуч, читати і записувати символи, і, отже, поводиться аналогічно як і справжній комп'ютер. Ми на прикладах покажемо, що машина Тюрінґа має ті ж самі обчислювальні можливості, що і багато інших комп'ютерних моделей.

Розглянемо детальніше основні складові машини Тюрінґа.

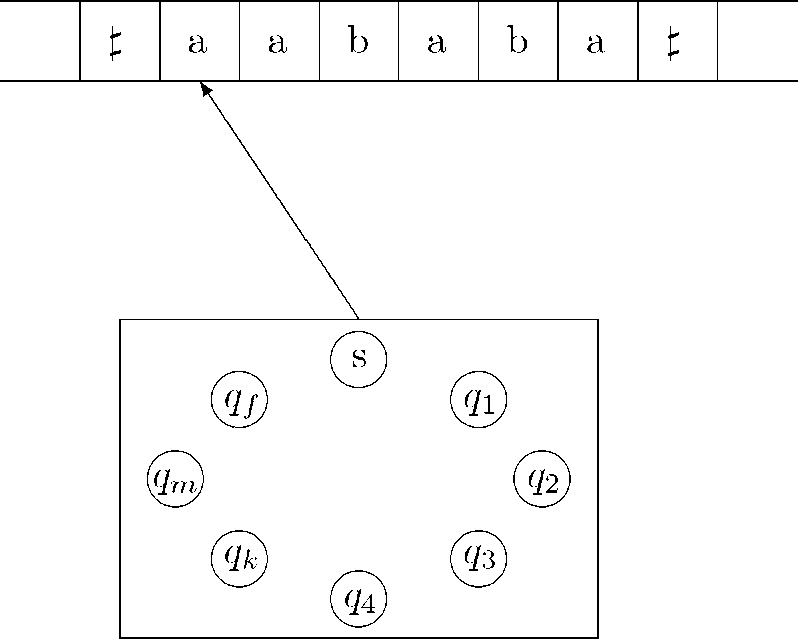
1. Стрічка використовується для збереження інформації. Вона поділена на комірки і є нескінченною в обидва боки. Комірки ні­яким чином не номеруються. Кожна комірка містить єдиний символ з скінченного алфавіту А. Символи алфавіту А діляться на три групи А = X Ц У Ц О. Букви алфавіту X називаються вхідними символами (з них утворються слова, які записані на стрічці перед початком ро­боти МТ). Через У позначається множина букв, які називаються ви­хідними символами (з них складаються слова, які записані на стрічці після завершення роботи МТ). О - множина допоміжних символів, до яких відноситься порожній символ Множини X та У можуть перетинатися.

2. Головка машини Тюрінґа може рухатися вздовж стрічки ко­мірка за коміркою, або праворуч, або ліворуч. Крім того, вона мо­же читати букву з комірки, яку аналізує, а також стирати букву і записувати в комірку нову букву. В кожний момент часу головка розміщується під однією з комірок стрічки і аналізує її вміст. Дана клітинка називається активною, а символ, який в ній знаходитиься - активним символом. Вміст клітинок, які не є активними головка МТ не аналізує і не бачить, які символи в них розміщені.

3. Головка машини Машини Тюрінґа контролюється керуючим пристроєм, який складається зі скінченної кількості станів. Серед них є два спеціальні стани: початковий і кінцевий. Початковий стан звичайно позначається через 5 або д₀, а кінцевий - через ду. Множину станів позначимо через В кожен момент часу керуючий пристрій перебуває в одному зі станів, які позначатимемо через д₁ ,д₂,... ,д_п. Перебуваючи в певному стані, МТ виконує деяку визначену операцію (наприклад, рухається праворуч, міняючи при цьому вміст клітинок на порожній символ #). Після того, як головка прочитає символ зі стрічки, керуючий пристрій визначає, яку дію виконувати (який сим­вол записувати і куди рухатися: праворуч чи ліворуч) і переходить в інший стан. МТ може виконувати тільки три елементарних дії: записувати в активну комірку новий символ, пересуватися на одну клітинку ліворуч або праворуч, переходити в новий стан. Жодних інших дій МТ виконувати не може! Тому більш складні дії повинні виражатися через елементарні. Ці дії описуються функцією переходів (програмою):

5 : ^ х А ^ д х А х{Ь,Е}.

Якщо для функції 5 виконується 5(д,а) = (р,Ь,Е) (чи, 5(д,а) = (р,Ь,Ь)), то це означає, що перебуваючи в стані д головка аналізує букву а (тобто буква а є активною), міняє її на Ь і рухається право­руч (відповідно ліворуч), керуючий пристрій при цьому переходить зі стану д у стан р. Описаний процес називається тактом роботи ма­шини Тюрінґа. Таким чином, МТ працює тактами, що визначаються функцією 5.

Програма МТ записується у вигляді наступної таблиці: