Лекція 4. Частково рекурсивні та примітив­но рекурсивні функції

В цьому парагрфі ми розглядатимемо функції / : N9 — N0, де N0 = N ЦІ {0}. Ми побудуємо клас всіх функцій такого виду з допомо­гою тільки трьох найпростіших функцій і двох операцій над такими функціями. Даний підхід до формалізації поняття алгоритму нале­жить Геделю. Основна ідея Геделя полягала в тому, щоб одержати всі обчислювальні функції із невеликої кількості базових функцій з допомогою найпростіших алгоритмічних засобів. Назвемо найпростішими такі функції:

• нуль-функцію: О(х) = 0, х Є N0;

• функцію наступності: 8(х) = х +1, х Є N0;

• функції проектування: РП (х₁ , , ... , і , . . . п ) — і , і ^Е N0.

До даних функцій будемо застосовувати такі операції.

Композиція. Нехай т,к Є N і нехай задано числові функції д : N9^ — N0 і Ні : N9 — N0, де і = 1,2,...,т. Визначимо функцію / : N — N0 за правилом

/ (т, ...,п_к) = д(Н1 (п1,.. .,п_к),..., Н_т (п1,.. .,п_к)).

Кажемо, що функція / одержана з допомогою операції композиції з функцій д і Н₁,..., Н_т. Функцію / позначимо через д о (Н₁,..., Н_т).

Примітивна рекурсія. Нехай к Є N0 і нехай задано числові функції д : N9 — N0 і Н : — N0 (в випадку, коли к = 0, функція

3. Приклад. Довести, що сталі функції С%(п₁ ,п₂,... ,п_к) = а, де к, а Є М₀, є примітивно рекурсивними.

Дані функції можна зобразити у вигляді скінченної кількості композицій примітивно рекурсивних функцій

С^к_а (п1 ,П2, ...,п_к) = 5 (5... (8(О_к (п1 ,П2,.. .,п_к)))...).

а

3. Приклад. Довести, що функція 5ита : М² ^ М₀, 8пта(и,т) = п + т є примітивно рекурсивною.

Функцію 5ита можна визначити наступним чином.

5ита(п, 0) = п = РІ (п),

8ита(и, т + 1) = п +(т + 1) = (п+т) + 1 = 5(Р₃³(п, т, 8ита(и, т))). Отже, 5ита є примітивно рекурсивною функцією, оскільки її одер­жано з примітивно рекурсивних функцій Р1 : М₀ ^ М₀ і 5 о Р3³ : М³ ^ М₀ з допомогою операції примітивної рекурсії.

3. Приклад. Довести, що функція Ргой : М² ^ М₀, Ртоії(и,т) = пт є примітивно рекурсивною.

Функцію Ргод, можна одержати з примітивно рекурсивних фун­кцій О і Бита о (Р| ,Р.³) з допомогою операції примітивної рекурсії наступним чином.

Ргоії(и, 0) = 0 = О(п), Ртой(и, т + 1) = п(т + 1) = пт + п = = 8ита(Р-₃³(п, т, Рго<і(п, т)), Р³(п, т, Рго<і(п, т))).

3. Приклад. Довести, що функція Ехр(п,т) = п^т є примітивно рекурсивною.

Функцію Ехр можна визначити як

Ехр(п, 0) = 1 = 5(О(п)), Ехр(п, т + 1) = п^т+1 = п^тп = = Ргод^Рз³(п, т, Ехр(п, т)),Р³(п, т, Ехр(п, т))).

3. Приклад. Довести, що функції

Г0 п = 0

а) Ргес : М₀ ^ М₀, Ргес(п) = п + 1 = < '

І п — 1,п > 0

І 0 п ^ ті

б) Міпиз : М² ^ М₀, Міпиз(п, т)= п + т = < ' ^_

п — т,п > т

в) А6й(п, т) = |п — т| є примітивно рекурсивними.

а) Функцію Ргес можна одержати з константи і проектування Р² : М² ^ М₀ з допомогою операції примітивної рекурсії.

Ргес(0) = 0, Ргес(т + 1) = т = Р_х² (т,Ргес(т)).

б) Функцію Міппй можна одержати з допомогою функції Ргес на­ступним чином.

МІППЙ(П, 0) = п = Р^ (П), Міппй(п, т + 1) = п + (т + 1) = (п + т) + 1 =

= Ргес(Р₃³(п, т, Міппй(п, т))).

в) А6й(п, т) = |п — т| = (п + т) + (т + п) =

= 5ита(Міпи5(п, т), Міпи«(т, п)).

Оскільки метою цього розділу є з допомогою вправ показати, що клас примітивно рекурсивних функцій є досить великим, то потібно довести, що булеві функції, які використовуються в мовах програ­мування високого рівня є примітивно рекурсивними. В наступних вправах розглядатимемо деякі булеві операції і відошення. Через 1 позначаємо значення "істина", через 0 - хибність.

4.8. Приклад. Показати, що наступні функції є примітивно рекур­сивними.

Ч лг / Ч (О, П > 1

^а) Ж^ед(п) = і

І 1, п = 0

б) Ап^(п,т) = < ,^П > ' т >

10, в протилежному випадку

І 1, п > 1 або т > 1

в) Ог(п, т) = <

0, в протилежному випадку

, _ „ . ₇ , , _ч |т,п > 1

г) I/-теп-еІ5е(п, т, к) = <

к, в протилежному випадку.

Дійсно, дані функції утворюються з примітивно рекурсивних фун­кцій наступним чином:

а) Жед(п) = Міпи«(1,п);

б) Ап^(п, т) = Жед(Жед(Рго^(п, т)));

в) Ог(п, т) = Жед(Ап^(Жед(п), Жед(т)));

г) I/-£^,еп-е/5е(п, т, к) =

= 5ита(Рго^(Жед(Жед(п)), т), Рго^(Жед(п), к))).

Надалі часто будемо писати "х ап^ у" замість Ап^(х, у), "х ог у" замість Ог(х,у), і "і£ х іЬеп у еІ8в £" замість //-£^,еп-е/5е(х, у, £).

9. Приклад. Довести, що наступні функції є примітивно рекур­сивними.

\ т-і / ч І 1,п = т

^а) Р^п ^т) = < _п .

0. 0, п = т

^ ^ ( \ /^1,п > ^т

^б) Сг⁽п ^т) = <

І 0, п < т

ч^ , ч /^1,п > ^т

^в) Сед^(п,т) =

І 0, п < т /^1,п < ^т

г) Ь5(п, т) = <

0. 0, п > т

1, п < т

д⁾ Ред^(п,т) = <

0, п > т

Дійсно, дані функції утворюються з примітивно рекурсивних фун­кцій наступним чином:

а) Рд(п, т) = Жед(А^(Міпп5(п, т), Міпи5(т, п)));

б) Сг(п, т) = Жед(Жед(Міпи5(п, т)));

в) Сед(п, т) = Сг(п, т) ог Рд(п, т);

г) Р5(п, т) = Жед(Сед(п, т));

д) Ред(п, т) = Жед(Сг(п, т)).

9. Приклад. Довести, що для кожного к Є N функція

Мах^к (п₁, п₂,...,п_к) = тах{п₁, п₂,..., п_к }

є примітивно рекурсивною.

Доведемо дане твердження індукцією по к. Для к = 1 тверджен­ня вірне, бо Мах¹ (п₁) = Р^ (п₁). Припустимо, що твердження вико­нується для к - 1 і доведемо для к: Мах^к (п₁,..., п_к) =

= і£ п_к > Мах^к-1 (п₁ ,...,п_к-1) іЬеп п_к еІ8е Мах^к-1 (п₁ ,...,п_к-1).

4.11. Приклад. Застосувати операцію примітивної рекурсії до фун­кцій д : N0 ^ N0 і Н : N3 ^ N0.

а) д(п) = 3^п, Н(пі,П2,пз) = 4п₂ + П3;

б) д(п) = 2^п, Н(п₁ ,п₂,п₃) = 3^П1 пП¹ (вважаємо, що 0⁰ = 1).

а) /(п, 0) = д(п) = 3^п

/(п, т + 1) = Н(п, т, /(п, т)) = 4т + /(п, т) /(п, 1) = 4 • 0 + /(п, 0) = 3^п /(п, 2) = 4 • 1 + /(п, 1) = 4 + 3^п /(п, 3) = 4 • 2 + /(п, 2) = 4 • 2 + 4 • 1 + 3^п Доведемо індукцією по т, що

/ (п,т) = 4((т - 1) + ... + 2 + 1) + 3^п = 4 ^(т-₂¹⁾⁺¹ (т - 1) + 3^п = = 2т(т - 1) +3^п.

Припустимо, що твердження виконується для т = к, тобто /(п, к) 2к(к - 1) +3^п.

Для т = к+1 маємо /(п, к+1) = 4к+/(п, к) = 4к+2к(к-1)+3^п = 2к(2 + к - 1) + 3^п = 2(к + 1)к + 3^п.

Таким чином, для будь-яких п,т Є N0

/(п,т) = 2т(т - 1) + 3^п

Функція / отримана з примітивно рекурсивних функцій д і Н з допомогою операції примітивної рекурсії і, отже, є примітивно ре­курсивною.

б) /(п, 0)= д(п) = 2^п

/(п, т + 1) = Н(п, т, /(п, т)) = 3^п(/(п, т))^п

₂

/(п, 1) = 3^п(/(п, 0))^п = 3^п2^п

2 2 3 2 3

/(п, 2) = 3^п(3^п2^п )^п = 3^п3^п 2^п = 3^п+^п 2^п

23 2 3 4

/(п 3) 3п(3П+П 2П )п 3П+П +п 2П

Доведемо індукцією по т, що / (п,т) = 3п+п²+...п^т 2п^т+1 =3 ^^ 2п^т+1.

Припустимо, що твердження виконується для т = к, тобто /(п, к)

_{3 2}п^к+1,

Для т = к + 1 маємо

п(п^к-1) к+1_ч п²(п^к-1) к + 2 —^ї оп ^ \п — 9П9 ^Тї оп ^

/(п, к+1) = 3^п(/(п,к))^п = 3^п(3 п-1 2^п )^п = 3^п3 п-1 2

, п²(п^к-1) _к + ₂ п²-п + п^к + ²-п² _к + ₂ п(п^к + ¹ -1) _к + ₂

3^п+ п-1 ⁾ 2^п = 3 2^пк+2 = = 3 ⁽ п-1 ⁾ 2^пк+2.

Таким чином, для будь-яких п,т Є М₀

п(п^т-1) т+1

/(п, т) = 3 п-і 2^П .

Функція / отримана з примітивно рекурсивних функцій д і Н з допомогою операції примітивної рекурсії і, отже, є примітивно ре­курсивною.

Мінімізація. Розглянемо частково визначену функцію п-змінних / (х₁ ,х₂,..., х_п). Визначимо функцію д (х₁ ,...,х_п) так. Зафіксуємо певні значення х₁ ,...,хі_₁ ,х_і +₁ ,...х_п п — 1 аргументів функції / та розглянемо рівняння /(х₁ ,...,х_і_₁ ,у,х_і +1 ,...,х_п) = хі. Обчи­слюватимемо послідовно значення / (х₁,..., х_і_₁, у, х_і+₁,..., х_п) для у = 0,1, 2,.... Позначимо через

а = тіп{у | / (х1,.. .,х-_1 ,у,х-+1, ...,хп) = хі }.

Зазначений процес є нескінченним у таких випадках:

• значення /(х₁,... ,х_і_₁, 0, х_і +₁,... ,х_п) не визначено;

• значення / (х₁,..., х _і _₁ ,у, х _і+₁ ,..., х_п) для у = 0,1,... ,а — 1 визначено, але вони відмінні від х а значення /(х₁,..., х,і_₁, а, х,і +₁,..., х_п) не визначено;

• значення / (х₁,..., х _і _₁, у, х _і +₁,... ,х_п) визначено для всіх у = 0, 1 , . . . , причому вони відмінні від х .

В усіх цих випадках значення функції д(х₁ ,...,х_п) вважають невизначеним. У решті випадків зазначений процес зупиняється і дає найменший розв'язок у = а рівняння /(х₁,..., х_і_₁, у, х_і+₁,..., х_п) = хі, який є значенням функції д(х₁,... ,х_п) = о,. Значення функції д для заданої функції / залежить від значень параметрів х₁,... ,х_п, тому функція д є частково визначеною функцією змінних х₁,... ,х_п. Кажуть, що функція д отримана з функції / з допомогою операції мінімізації за змінною х_і .

Функцію / називають частково рекрсивною, якщо вона може бу­ти утворена з найпростіших функцій за допомогою скінченної кіль­кості застосувань операцій композиції, примітивної рекурсії та міні­мізації. Всюди визначені частково рекурсивні функції називаються загальнорекурсивними.

4.12. Приклад. Розглянемо функцію / : М₀ ^ М₀, /(х) = х + 2. За допомогою операції мінімізації визначимо функцію д : М₀ ^ М₀. Для цього розглянемо рівняння у + 2 = х. Отже, функцію д не визначено, якщо х = 0 або х = 1, і д(х) = х — 2, якщо х > 2.

13. Приклад. Доведемо, що функція д : N0 х N0 — N0,

д^(х1, ^х2⁾ = _{1 —} ^012

є частково рекурсивною. Застосуємо операцію мінімізації за змінною х₂ до примітивно рекурсивної функції /(х₁ ,х₂) = (1 + х₁ )х₂. В ре­зультаті отримаємо рівняння (1 + х₁ )у = х₂. Отже,

х₂, х₁ = 0,

д(х1 ,х2 )={0,х2 =0, = - .

1 — х₁ х2⁰¹²

Т, х₁ = 0 і х₂ = 0,

В даному параграфі ми показали, що клас частково рекурсивних функцій є досить широкий. Поняття частково рекурсивної функції - одне з основних понять теорії алгоритмів. Його значення є таким. З одного боку, кожна стандартно задана частково рекурсивна функція є обчислювана за певною процедурою, яка відповідає інтуїтивному уявленню алгоритму, а з іншого - які б досі не будувалися класи то­чно визначених алгоритмів, завжди з'ясовувалося, що числові фун­кції, які обчислювалися за алгоритмами цих класів, були частково рекурсивними. Тому загальноприйнятою є така наукова гіпотеза:

Теза Черча. Клас алгоритмічно обчислюваних частково визначе­них числових функцій збігається з класом усіх частково рекурсив­них функцій.

У формулювання цієї тези входить інтуїтивне поняття обчислю- ваності, тому його не можна ні довести, ні спростувати в загаль- номатематичному значенні. Це факт, на користь якого свідчить ба­гаторічна математична практика. Проте, справедливою є наступна теорема, доведення якої читач може знайти в [?]:

13. теорема. Функція є обчислюваною за Тюрінґом тоді і тільки тоді, коли вона є частково рекурсивною.

Вправи до лекції 4.

4.1. Довести, що наступні функції однієї змінної є примітивно ре­курсивними:

а) /(п) = п;

б) д(п) = 3п + 4;

в) д(п) = 2^П + п²;

г) д(п) = п!;

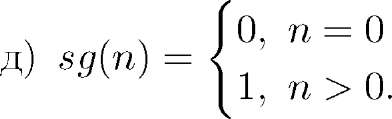
2. Довести, що наступні функції / : N0 — М₀ є примітивно ре­курсивними:

а) /(п, т) = тіп{п, т};

б) /(п, т) = тах{п, т}.

2. Застосувати операцію примітивної рекурсії до функцій д : М₀ — М₀ і к : М³ — М₀. Записати результуючу функцію / : М² — М₀ аналі­тично.

а) д(п) = 2^П, к(пі,П2,пз) = 3п2 + Пз;

б) д(п) = 2012п²⁰¹², к(п₁ ,п₂,п₃) = 5п₂ + п₃;

в) д(п) = 3^П, к(п₁ ,п₂,п₃) = 2п₁ + 5п₃;

г) д(п) = 2012^п, к(п₁ ,п₂,п₃) = 5^П1 п^¹ (вважаємо, що 0⁰ = 1);

д) д(п) = 2^П + п², к(п1 ,П2,П3) = щ + ЗП3;

е) д(п) = 1, к(п1 ,П2,П3) = П3($д|п1 + 2 — 2п31).

2. Застосувати операцію мінімізації до функції / за всіма її змін­ними. Подати вихідні функції д аналітично.

а) /(п) = 2;

^г) д^(п) = ;

д⁾ д⁽п^,т) = т+2.

б) /(п) = [§];

в) /(п, т) = п + т;

г) /(п, т) = 2 — п — т;

д) /(п, т) = Р1²(п, т);

е) /(п, т) = тах{п, т}; є) /(п, т) = тіп{п, т};

ж) /(п, т) = п + т.

4.5. Застосувавши операцію мінімізації до відповідної примітивно рекурсивної функції /, довести, що функція д частково рекурсивна:

а) д(п) =3 — п;

6. Довести, що застосувавши один раз операцію мінімізації до всюди визначеної числової функції, отримаємо функцію, яка визна­чена принаймі в одній точці.

7. Навести приклад функції / : N0 ^ N0, застосувавши до якої операцію мінімізації двічі, отримаємо ніде не визначену функцію.

8. Сформулювати необхідну і достатню умову того, що функція д, отримана з функції / з допомогою операції мінімізації є

а) всюдивизначеною;

б) ніде не визначеною.

Лекція 5. Нормальні алгоритми Маркова. Ана­ліз НАМ.

В даному параграфі розглядається ще один важливий підхід до уточнення поняття алгоритму, розроблений А.А. Марковим. Нор­мальні алгоритми Маркова (НАМ) базуються на перетворенні слів в деякому скінченному алфавіті в відповідності з певним чином ви­значеними правилами. В НАМ використовується тільки одна елемен­тарна дія - підстановка, яка визначається наступними чином. Нехай А = {а₁, а₂,..., а_п} - алфавіт. Якщо а і в - слова в алфавіті А, то вирази а ^ в і а ^ в називаються формулами підстановки в алфавіті А (вважаємо, що символи ^ та ^ не належать алфавіту А). При цьому формула а ^ в називається звичайною формулою підстановки, а формула а ^ в заключною формулою підстановки. Сама підстановка (як дія) задається формулою підстановки і засто­совується до слів ш в алфавіті А. Суть операції а ^ в (а ^ в) полягає в відшуканні в слові ш найлівішого входження підслова а і заміні цього підслова на слово в. При цьому інші частини слова ш залишаються незмінними. Якщо ліва частина формули підстановки входить в слово ш, то кажуть, що дана формула застосовна до слова ш. В іншому випадку кажемо, що формула підстановки незастосов­на до слова ш і в цьому випадку підстановка не виконується. Якщо права частина формули підстановки - порожнє слово (яке в НАМ не познається ніяким символом), то підстановка а ^ зводиться до за­креслення підслова а в слові ш. Домовимося, що якщо в лівій частині формули підстановки є порожнє слово, то підстановка ^ в полягає в

дописуванні зліва до слова ш слова в. Зауважимо, що згідно означе­ння, формула з порожньою лівою частиною застосовна до будь якого слова.

1. Приклад. Нехай для слів в алфавіті А = {а, Ь, с} задані наступні підстановки:

а) аЬ ^ ас;

б) аЬс ^ Ьа;

в) Ьа

г) Ь ^ с.

Застосуємо кожну з них до слова аЬЬасЬа.

Для застосування марківської підстановки до слова ш необхідно знайти найлівіше входження в ш лівої частини підстановки. У випад­ку а) слово аЬ тільки раз входить в слово аЬЬасЬа, тому в результаті підстановки одержуємо слово асЬасЬа. Оскільки слово аЬс не є підсло- вом слова аЬЬасЬа, то підстановка з пункту б) не застосовна до даного слова. У пунктах в) та г) ліві частини підстановок входять декілька раз у слово аЬЬасЬа, а тому застосовуємо підстановки до першого вхо­дження їх у вхідне слово. Отримаємо слова аЬсЬа і аЬасЬа відповідно.