Міністерство освіти і науки України

Прикарпатський національний університет імені Василя Стефаника

Володимир Гаврилків

Елементи теорії алгоритмів, формальних мов та автоматів в прикладах і задачах

Івано-Франківськ 2011

© Володимир Гаврилків, 2011.

		Зміст
Розділ I.	Формальні мови		4
Лекція	1.	Вільні напівгрупи і формальні мови	4
Лекція	2.	Системи числення. Дії над системними числами.	9
Лекція	3.	Регулярні мови і регулярні вирази	22
Лекція	4.	Формальні породжувальні граматики	29
Розділ II.	Скінченні автомати		39
Лекція	1.	Автомати. їх типи та задання	39
Лекція	2.	Детерміновані скінченні автомати без виходу	49
Лекція	3.	Недетерміновані скінченні автомати без виходу	58
Лекція	4.	Перетворення НСА до ДСА	64
Лекція	5.	Скінченні автомати і регулярні мови. Лема про
		роздування.	71
Лекція	6.	Автомати з магазинною пам'яттю	79
Розділ III		Формальні алгоритмічні моделі	86
Лекція	1.	Машина Тюрінґа. Аналіз МТ.	86
Лекція	2.	Алгоритми синтезу МТ	95
Лекція	3.	Функції, що обчислюються МТ	107
Лекція	4.	Частково рекурсивні та примітивно рекурсивні
		функції	119
Лекція	5.	Нормальні алгоритми Маркова. Аналіз НАМ.	128
Лекція	6.	Синтез нормальних алгортмів Маркова	135
Лекція	7.	Нормально обчислювані функції. Композиція
		НАМ	143
Лекція	8.	Складність алгоритмів	151

Розділ I

Формальні мови

Лекція 1. Вільні напівгрупи і формальні мо­ви

Нехай X - довільна множина. Бінарною операцією на множині X називається відображення * : X х X ^ X, де X х X - множина всіх впорядкованих пар елементів з X. Образ в X елемента (а,Ь) Є X х X позначатимемо через а * Ь або просто через аЬ. Непорожня множина X, наділена бінарною операцією * : X х X ^ X називається групо- їдом. Бінарна операція * на множині X називається асоціативною, якщо а(Ьс) = (аЬ)с для всіх а,Ь,с Є X. Якщо операція * є асоціа­тивною на X, то пара (X, *) називається напівгрупою. Нехай (X, *) і (У, о) - напівгрупи. Гомоморфізмом з X в У називається таке від­ображення ^ : X ^ У, що <р(а * Ь) = р(а) о р(Ь) для всіх а,Ь Є X.

Нехай X - непорожня множина, яку називатимемо (формаль­ним) алфавітом, елементи якої будемо називати буквами (символа­ми, знаками). Якщо IX | = 2, то алфавіт називається бінарним або двійковим. Найчастіше бінарний алфавіт позначається через В = {0,1}.

1.1. Приклад. Алфавіт X формул алгебри висловлень є об'єднан­ням X = XI ЦІ X2 ЦІ Xз, де множина XI = {р, д,г,...} містить про- позиційні змінні, X₂ = {Л, V, —} - логічні зв'язки, а множина

Xз = {(,)} складається з допоміжних символів (дужок).

Визначимо слово (ланцюг) в алфавіті X як непорожню скінченну послідовність х\х₂ ... х_т елементів з X. Наприклад, 010111 - слово в бінарному алфавіті В, а р Л д ^ г - слово в алфавіті X з прикладу 1.1. Таким чином, два слова хіх₂ ... х_т і у\у₂ ... у_п дорівнюють тоді і тільки тоді, коли вони співпадають як послідовності, тобто коли т = п і хі = уі,...,х_т = у_т.

Алфавіти позначатимемо великими буквами латинського алфа­віту, наприклад А, В, С, X і т.д. Букви формального алфавіту буде­мо позначати малими буквами латинського алфавіту: о,, Ь, с і т.д., а слова - малими буквами грецького алфавіту, наприклад, а, в, и.

Через X + позначимо множину всіх слів в алфавіті X. Напри­клад, якщо X - бінарний алфавіт {0,1}, то

X + = {0,1,00, 01,10,11, 000, 001,...}. На множині X+ всіх слів визначимо бінарну операцію:

Х1Х2 ...Х_т О Уі У2 ...у_п = Х1Х2 . . . Х_т уі у₂ . . . Уп.

Ця операція на X + іноді називається конкатенацією, вона, очеви­дно, асоціативна, і (X +, о) називається вільною напівгрупою на мно­жині X. Вільну напівгрупу з множиною твірних X позначають часто також через Р(X) (від англійського слова "£гее" - вільний).

Поряд з вільною напівгрупою X+ над алфавітом X часто роз­глядають вільний моноїд X* = X + У{е} над X, в якому одиниця е є порожнім словом, яке не містить жодної букви.

Слово, яке містить і букв (слів) а позначатимемо через а^г. На­приклад, а¹ = а (ми ототожнюємо, таким чином, букву а з словом, що містить єдину букву а), а² = аа, а⁰ = е - порожнє слово е. Обер­ненням слова х (позначається через х^Е) називається слово, записане в оберненому порядку, тобто якщо х = а₁ ... а_п, де всі а,_і - букви, то х^Е = а_п ... а₁. Крім того, е^Е = е. Легко перевірити, що (ху)^Е = у^Ех^Е.

Нехай а, в і 7 - довільні слова в деякому алфавіті X. Назвемо а префіксом слова ав, а в - суфіксом слова ав. Слово в називатимемо підсловом слова ав7. Префікс і суфікс слова є його підсловами. На­приклад, Ьа - префікс і підслово слова Ьас. Відмітимо, що порожнє слово є префіксом, суфіксом і підсловом довільного слова.

Якщо а = в і а - префікс (суфікс) слова в, то а називається власним префіксом (суфіксом) слова в. Довжина слова - це кіль­кість букв в ньому, тобто якщо и = а₁ ... а_п, де всі а - букви, то довжина слова и дорівнює п. Довжину слова и позначатимемо через |и|. Наприклад, |ааЬ| =3 і |е| =0.

Формальною мовою в алфавіті X називається довільна множина слів в X, тобто довільна підмножина вільного моноїда X*. Напри­клад, множина 0 - це формальна мова. Множина {е}, яка містить тільки порожнє слово, також є мовою. Відмітимо, що 0 і {е} - дві різні формальні мови. Іншим прикладом формальної мови є мова Ь, що містить всі слова, які складаються з нуля і більше букв о,. її мо­жна позначити через {а : і > 0}. Ясно, що Ь = {а}* (для спрощення {а}* позначатимемо надалі через а*).

Якщо мова Ь така, що ніяке слово в Ь не є власним префіксом (суфіксом) ніякого іншого слова в Ь, то кажуть, що Ь має префіксну (суфіксну) властивість. Наприклад, а* не має префіксної властиво­сті, а {а^гЬ : і > 0} має.

Оскільки формальна мова Ь - це множина (підмножина X*), то до формальних мов можна застосовувати операції об'єднання, пере­тину, знаходження різниці і доповнення. Операцію конкатенації мо­жна застосувати до мов таким же чином, як і до слів.

Нехай Ь₁ - мова в алфавіті Хі, а Ь₂ - мова в алфавіті Х₂. Тоді мова Ь₁Ь₂, яка називається конкатенацією (добутком) мов Ь₁ і Ь₂, - це формальна мова {ш₁ ш₂ : ш₁ Є Ь₁ ,ш₂ Є Ь₂}.

Ітерація (замикання Кліні) мови Ь, яка позначається через Ь*, визначається наступним чином:

1. £⁰ = {е},

2. Ь^п = ЬЬ^п-1 для п > 1,

3. Ь* = Уп>о£^п.

Розглянемо деякі приклади.

1.2. Приклад. Покажемо, що формальна мова {0,10}* складається зі слів, які не містять підслова 11 і закінчуються на 0.

Очевидно, що конкатенація довільної кількості 0 та 10 закінчу­ється на 0. Вона не може породити підслово 11, оскільки кінці обох слів 0 та 10 розділюять довільні дві 1 в їхній конкатенації.

Нехай ш - слово в алфавіті {0,1}, яке не містить підслів 11 і за­кінчується на 0. Якщо ш не містить входжень 1, то ш є конкатенацією |ш| букв 0, і, отже, ш Є {0, Ю}¹^¹ С {0,10}*. Припустимо, що слово ш містить п > 1 входжень букв 1 . Тоді, після кожного входження букви 1 в ш мусить слідувати буква 0, бо інакше буква 1 або слідує за 1, або є останньою буквою слова ш, що суперечить припущенню. Таким чином, слово ш запишеться як

0 ... 0(10)0 ... 0(10)0 ... 0(10)0... 0,

де вираз 0 . . . 0 означає нуль або більше входжень букви 0. Отже, ш є конкатенацією слів 0 та 10, тобто ш Є {0,10}*.

Для мови Ь визначимо обернену мову як Ь^Е = {ш^д : ш Є Ь}.

3. Приклад. Доведемо, що для формальних мов А і В виконую­ться рівності (АВ)^н = В^нА^н та (А У В)^н = А^н У В^н.

Дійсно, (АВ)^п = {ш^п | ш Є АВ}={(ав)^п | а Є А, в Є В}={в^па^п | а Є А, в Є В}={в^н | в Є В} • {а^н | а Є а}=В^нА^н.

Аналогічно, (А У В )^п={ш^п | ш Є А У В} = {ш^п | ш Є А}У{ш^п | ш Є В}=А^Е У В^Е.

3. Твердження. (Лема Ардена) Нехай А і В - дві мови, при­чому е Є А, і мова X задовольняє рівність X = АХ У В. Тоді, X = А* В.

Доведення. Доведемо за індукцією, що X С А*В. Спершу, розгля­немо випадок ш = е. Якщо ш Є X, то ш Є АX У В. Оскільки е Є А, то необхідно ш Є В і, отже, ш Є А*В.

Далі, припустимо, що для всіх слів ш довжини менше п викону­ється, що якщо ш Є X, то ш Є А*В, і розглянемо слово а довжини п. Якщо а Є X = АX У В, то або а Є В С А*В або а = ві для де­яких в Є А і і Є X .В другому випадку мусить виконуватися в = е і, отже, |і| < |а|. Отже, за індуктивним припущенням, і Є А*В і а Є АА*В С А*В. Цим завершується індуктивний крок і, отже, X С А*В.

Щоб довести протилежне включення, використаємо індукцію, щоб показати, що А^пВ С X для всіх п > 0. Для п = 0, ми ма­ємо, що А⁰ В = В С АX У В = X. Для п > 0 за індуктивним припущенням виконується А^пВ = А(А^П-1 В) С АX. Таким чином, А^п ^А^А^В = X. □

1.5. Приклад. Нехай формальні мови А, В С {а, 6}* задовольняють рівності:

А = {е} У {а}А У {6}В, В = {е} У {6}В. Знайти прості зображення мов А і В.

Застосуємо лему Ардена до другого рівняння і знайдемо мову В = {6}*{е} = {6}*. Далі, аналогічно знаходимо мову А = {а}*({е}Ці {6}В).

Наостанок, підставимо {6}* замість В і одержуємо: А = {а}* ({е}и{6}{6}* ) = {а}* {6}*.

Нехай Х\ і X₂ - алфавіти і Н : X₁ ^ X* - довільне відображення. Відображення Н можна продовжити до гомоморфізму Н : X* ^ X*, покладаючи Н(е) = е і Н(ша) = Н(ш)Н(а) для всіх ш є X* і а Є Хі. Застосовуючи гомоморфізм до мови Ь, ми одержимо іншу мову Н(Ь), яка є множиною слів {Н(ш) : ш Є Ь}.

1.6. приклад. Припустимо, що ми хочемо замінити кожне входже­ння в слово букви 0 на букву а, а кожне входження 1 на 66. Тоді можна визначити гомоморфізм Н так, що Н(0) = а і Н(1) = 66. Якщо Ь = {0^П1^П : п > 1}, то Н(Ь) = {а^п6^2п : п > 1}.

Вправи до лекції 1.

1. Визначте формальні алфавіти для запису:

а) арифметичних виразів;

б) азбуки Морзе.

2. Визначте довжину слова а = "математика" в українському алфавіті.

3. Які з наведених слів є підсловами слова ш="індустралізація": а₁ = "індус", а₂="індустрія", а₃="ліза", а₄="акція"?

4. Випишіть всі (власні) префікси, суфікси і підслова слова оЬс.

5. Скільки формальних мов можна побудувати на алфавіті X = {0,1, 2,3}, в яких довжина кожного слова не перевищує 3?

6. Скільки слів довжини п можна побудувати в алфавіті, що мі­стить к букв? Скільки формальних мов можна утворити з цих слів?

7. Знайдіть всі слова в алфавіті {0,1}, які задовольняють рівність х011 = 011х.

8. Чи правда, що якщо формальна мова А містить п слів, а мова В - т слів, то АВ мусить містити пт слів?

9. Нехай А = {(01)^п : п > 0} і В = {01, 010}. Знайти А У В, А П В, А \ В, В \ А, АДВ, АВ і АВА.

10. Нехай А = {пра, е}, В = { дід, баба }. Знайти АВ і А*В.

11. Чи може мова Ь* або Ь⁺ бути порожньою? За яких умов мови Ь* і Ь⁺ є скінченними?

12. Знайти слово найменшої довжини в алфавіті {0}, яке не на­лежить формальній мові {е, 0, 0², 0⁵}³.

13. Довести рівність: (А У В)* = А*(ВА*)*.

14. Нехай А і В - формальні мови. Довести або спростувати рів­ності:

    1. (А^н)* = (А*)^н;

    2. (а+ )* = А*;

    3. (А У А^н)* = А* У (А*)^н

    4. А² У В² = (А У В)²; б) А* П В * = (А П В )*.

15. Які з наступних мов мають префіксну (суфіксну) власти­вість?

1) 0;

2. {е};

3. {а^п6^П : п > 1};

4. Ь*, якщо Ь має префіксну властивість;

5. {ш : ш Є {а, 6}* і кількість букв а в ш дорівнює кількості букв 6}.

16. Нехай Н - гомоморфізм, визначений рівностями Н(0) = а, Н(1) = 66 і Н(2) = е. Опишіть формальну мову Н(Х), де X = {012}*.

Лекція 2. Системи числення. Дії над систем­ними числами.

В приладах дискретної дії інформація зображується в вигляді слів (формальної мови) в деякому скінченному алфавіті. При прое­ктуванні автоматичних перетворювачів інформації виникає пробле­ма вибору для них алфавіту і, в першу чергу, кількості букв в алфа­віті.

В загальному випадку для перетворення інформації потрібно обра­ти три алфавіти: вхідний, внутрішній та вихідний. Вхідний і вихі­дний алфавіти використовуються для обміну інформацією перетво­рювача з зовнішнім середовищем і визначаються специфікою цього середовища і класом розв'язуваних задач. Наприклад, для "розмо- ви"людини з машиною найбільш зручним є звичайний буквенний (наприклад, український) алфавіт. Якщо клас розв'язуванх задач обмежується математичними задачами, то достатньо використову­вати формальну мову формул і десяткових цифр. Щоб виконати ав­томатичну переробку інформації, слова вхідного алфавіту перетво­рюються в слова внутрішнього алфавіту, в якому працює перетво­рювач. Вибір внутрішнього алфавіту суттєво впливає на складність перетворювача інформації і ефективність його роботи. В більшості кібернетичних приладів використовується бінарний (двобуквенний) алфавіт, який є дуже зручним для виконання арифметичних і логі­чних операцій.

Після вибору алфавіту виникає задача визначення раціонально­го способу кодування інформації словами в даному алфавіті. Універ­сальний автоматичний перетворювач інформації повинен виконувати будь-які алгоритми. Тому перетворювана інформація може бути ду­же різного характеру. Однак в теорії алгоритмів доведено, що будь- який алгоритм може бути зведений до обчислювального алгоритму. В зв'язку з цим в універсальних претворювачах, як правило, засто­совується числове кодування інформації. В цифрових обчислюваль­них машинах будь-яка інформація зображується в вигляді строго визначеної послідовності цифр. Кожній такій послідовності можна поставити в відповідність певне число і звести, таким чином, будь- яке перетворення інформації до операцій над числами. В зв'язку з вищесказаним в даному параграфі ми детально зупинимося на різних числових системах.

Система числення (англ. пишЬег (пишегаііоп) 8у8Іеш, поіаііоп) - це сукупність способів і засобів запису чисел для проведення під­рахунків.

Найпростішою системою числення є унарна система числення, в якій кожне натуральне число зображується відповідною кількістю деяких символів. Наприклад, якщо вибрати символ "|", то натураль­не число сім запишеться у вигляді |||||||. Унарна система числення

використовується для запису малих чисел і має застосування в тео­рії алгоритмів.

2.1. Типи систем числення. Розрізняють такі типи систем числення: позиційні, непозиційні та змішані. Найбільш поширени­ми є позиційні системи числення. У позиційних системах числення одна і та ж цифра (числовий знак) у записі числа набуває різних значень залежно від своєї позиції. Кожна позиція з присвоєним їй порядковим номером називається розрядом числа. Домовимося про наступну нумерацію розрядів: якщо число має п розрядів цілої і т розрядів дробової частини, то старшому розряду цілої частини при­своюється номер п — 1, молодшому розряду цілої частини - номер 0, старшому розряду дробової частини - номер -1, а молодшому розря­ду - номер -т. В позиційних системах числення кожному розряду присвоюється відповідна вага. Найчастіше застосовуються позицій­ні системи числення, в яких і-му розряду присвоюється вага д^і, де д Є Ж. Ціле число д при цьому називають основою системи числення. Значення числа за його зображенням визначається за формулою:

п—1

(1) (ап—і «п—2 ...аі ...аі ао, а—і а—2 ...а—т )д = ^^ аі д^і =

і=—т

ап—ід^п—і+ап—2д^п—2 + .. .+аід^і+.. .+аі д+аод°+а—і д^—і + .. .+а—тд^—т

В лівій частині формули (2.1) записано символічне зображення числа. Тут а_і (і = п — 1,п — 2,..., —т) - символи, які позначають цілі числа.

2.1. Приклад. Обчислимо значення числа 10(—1)(—1), 01 в системі числення з основою 3 і символами —1, 0 та 1. В цьому випадку кіль­кість цілих розрядів п = 4, а кількість дробових розрядів т = 2. З допомогою формули (2.1) одержуємо:

10(—1)(—1), 01 = 1 • З³ + 0 • 3² + (—1) • 3 + (—1) +0 • 3^—і + 1 • 3^—2 = 23¹.

9

Найчастіше (хоча і не завжди) символи а_і позначають цілі чи­сла натурального ряду від нуля до д — 1 і називаються цифрами даної системи числення, а сама система числання називається д- ковою системою числення. В д-ковій системі числення кількість рі­зних цифр дорівнює основі д системи числення. Наприклад, в зви­чайній арабській (десятковій) системі числення використовуються цифри 0,1, 2,3, 4, 5, 6, 7, 8, 9. Права частина формули (2.1) визначає правило обчислення числового значення символічного запису лівої частини цієї формули. Можна вважати, що ліва частина формули (2.1) є шифром числа, а права частина визначає алгоритм дешифру­вання даного шифру.

У непозиційних системах числення величина, яку позначає ци­фра, не залежить від її позиції у числі. При цьому система може накладати обмеження на позиції цифр, наприклад, щоб вони були розташовані по спаданню, чи згруповані за значенням. Проте, це не є принциповою умовою для розуміння записаних такими системами чисел.

Типовим прикладом непозиційної системи числення є римська система числення. Дана система числення базується на використанні особливих знаків для десяткових розрядів, а саме, в якості цифр у ній використовуються латинські букви:

Римська цифра	Десяткове значення
I	1
V	5
X	10
Ь	50
С	100
Б	500
М	1000

Натуральні числа записуються за допомогою повторення цих цифр. При цьому, якщо більша цифра стоїть перед меншою, то вони додаються (принцип додавання), якщо ж менша — перед більшою, то менша віднімається від більшої (принцип віднімання). Останнє правило застосовується тільки для уникнення чотириразового по­вторення однієї цифри. Наприклад, І, X, С ставляться відповідно перед X, С, М для позначення 9, 90, 900 або перед V, Ь, О для по­значення 4, 40, 400. Наприклад, VI = 5 + 1 = 6, IV = 5 - 1 = 4, XIX = 10 + 10 - 1 = 19 (замість XVIII!), ХЬ = 50 - 10 = 40, XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 тощо.

Римські числа використовувалися стародавніми римлянами. Ви­конання арифметичних дій над багатозначними числами в цій систе­мі дуже незручне. Ця система числення на сьогодні майже не засто­совується. Сьогодні з допомогою таких чисел позначають століття (XV ст.), роки н.е. (МСМЬХХУЇЇ) та місяці в датах (1.УЛ975), по­рядкові числівники, а також похідні невеликих порядків (у^ІУ, у^у). Часто римські числа використовують також із естетичною метою.

Змішана система числення є узагальненням системи числення з основою д і її часто відносять до позиційних систем числення. Осно­вою змішаної системи є послідовність чисел, що зростає, {Ьк}£=₀ і кожне число х зображується як лінійна комбінація: х = ^П=₀ ^ак Ьк, де на коефіцієнти ак (цифри) накладаються деякі обмеження. Якщо Ьк = д^к для деякого д, то змішана система співпадає з д-ковою си­стемою числення.

Найвідомішим прикладом змішаної системи числення є зображе­ння часу у вигляді кількості діб, годин, хвилин і секунд. При цьому величина ії днів Н годин т хвилин 5 секунд відповідає значенню ії • 24 • 60 • 60 + Н • 60 • 60 + т • 60 + 5 секунд.

Цікавим прикладом є система числення майя. Майя використо­вували двадцяткову систему числення за одним винятком: у другому розряді було не 20, а 18 ступенів, тобто після числа (17)(19) відразу йшло число (1)(0)(0). Це було зроблено для полегшення розрахунків календарного циклу, оскільки (1)(0)(0) дорівнювало 360, що прибли­зно дорівнює кількості днів у сонячному році.

У нумізматиці особливо велику вагу мають десяткова, дванадця- ткова (дуодецимальна), четвертна та шісткова системи числення. У інформаційних технологіях застосовуються двійкова, десяткова, ві- сімкова, та шістнадцяткова системи числення.

2.2. Позиційні д-кові системи числення. Зупинимося деталь­ніше на д-кових позиційних системах числення. Спершу доведемо наступну лему.

2.2. Лема. Якщо а,д Є Ж і д > 0, то існують такі єдині числа 5, г Є Ж, що а = 5д + г, де 0 < г < д.

Доведення. Розглянемо множину всіх цілих чисел виду а — хд, де х Є Ж. Дана множина містить додатні елементи. Нехай г = а — 5д - найменший невід'ємний елемент цієї множини. Ми стверджуємо, що 0 < г < д. Дійсно, в протилежному випадку а — 5д > д, а тому

0 < а—(з+1)д < г, що суперечить мінімальності г. Доведемо єдиність даного зображення. Припустимо, що існує інший запис а = зд + з, де 0 < г < д. Тоді а = зд + г = зд + з, звідки (5 — з)д = г — г і —д < г — г < д. Оскільки г — г ділиться на д, то г — г = 0, а, отже, г = г і 3 = з. □

Нехай д Є N \ {1} - основа д-кової системи числення.

2.3. теорема. Кожне натуральне число т можна і притому єди­ним чином подати у вигляді

т = а,_п д^п + а,_п-\д^п-1 + ... + «і д + «о,

де а_і (0 < і < п) - певні цілі невід'ємні числа, менші від д, причому а,_п = 0.

Доведення. Згідно з лемою 2.2 для натуральних чисел т та д зна­йдуться такі єдині цілі числа з₀ і а₀, що т = з₀д + а₀ і 0 < а₀ < д. Оскільки д > 2, то 0 < з₀ < т. Якщо з₀ = 0, то теорема доведе­на, інакше існують такі єдині цілі числа з₁ і а₁, що з₀ = з₁ д + а₁, 0 < а₁ < д і 0 < з₁ <з₀. Продовжуючи даний процес аналогічно, одержимо строго спадну послідовність (зк) натуральних чисел. Да­на послідовність не може бути нескінченною, а тому існує таке п, що з_п-1 = 0, але з_п = 0. Звідси одержуємо, що з_п-2 = з_п-1 д + а_п-1 і з_п-1 = з_пд + а_п = а_п, де 0 < а_і < д. Тоді шуканий єдиний запис числа т матиме вигляд т = з₀д + а₀=(з₁ д + а₁ )д + а₀=з₁ д² + а₁ д +

а0 = .. .=зп-2д^п-1 + ап-2д^п-2 +... + «1 д + «0 =(зп-1 д + ап-1 )д^п-1 +

ап-2 д^п-2 +... + «1 д + «0=а_п д^п + ап-1 д^п-1 + «п-2 д^п-2 +... + «1 д + «0.

□

Можна довести, що для кожного додатнього дробового числа а так само, як і для кожного натурального числа, в системі числення з будь-якою основою д існує тільки єдиний запис виду

п

а = ^аід^і = ^апд^п + ... + аід^і +... + «0д⁰ + «-1 д^-1 + ... + а-тд^-т.

і=-т

Отже, запис числа а в системі числення з основою д - це зобра­ження числа у вигляді суми степенів основи д з цілими невід'ємними коефіціентами, меншими ніж основа д.

Вираз

а = а_п д^п + ... + а д^г + ... + ао д^о + а_і д^-1 + ... + а-т д_^т. скорочено записують так

а = (®п®п_і... а ... аіао, а_іа_2 ... а_т)д.

Введення знака мінус дає змогу записувати у системі числення з основою д також і від'ємні числа.

2.3. Арифметичні операції в різних системах числення.

При виконанні арифметичних операцій над числами, записаними в десятковій системі числення, ми користуємось правилами додаван­ня, віднімання і множення чисел "стовпцем"і ділення "кутом". За цими ж правилами виконують операції й над числами, записаними в будь-якій іншій системі числення. Доведемо, наприклад, правило додавання в системі числення з основою д. Нехай а = (ак ... а₁ а₀ )_д і Ь = (Ь₈ ...ЬіЬ₀)_д. Не втрачаючи загальності, можна вважати, що к > 8. Знайдемо суму а + Ь.

а + Ь = (а_к ... аі ао )д + (Ь₈... Ьі Ьо )д=(а_к д^к +... + а₈₊і д⁸⁺¹ + а₈ д⁸ + ... + аід + ао) + (Ь8д⁸ + ... + Ьід + Ьо)= акд^к + ... + а8+ід^8+і + (а8 + Ь8 )д⁸ + ... + (аі + Ьі )д + (ао + Ьо).

У цьому записі деякі з чисел а_о + Ь_о, а_і + Ь_і,... ,а₈ + Ь₈ можуть виявитися більшими або дорівнювати основі числення д. Якщо а_т + Ьт > д (0 < т < 8), то ат + Ьт = д + Гт, де 0 < Гт < д. Тому, (ат+і + Ьт+і)д^т+^і + (ат + Ьт)д^т = (ат+і + Ьт+і + 1)д^т+^і + Гтд^т. Замінивши кожен вираз (а_т + Ь_т) > д, починаючи з а_о + Ь_о і зкінчуючи а₈ + Ь₈, рівнозначним йому виразом д + г_т і перенісши там, де це потрібно, одиницю в наступний розряд, дістанемо запис суми а + Ь в системі числення з основою д:

_к

а + Ь = Ск д + ... + сі д + Со,

або скорочено а + Ь = (ск ... с_іс_о)_д.

Таким чином, щоб додати два цілі додатні числа, записані в си­стемі числення з основою д, потрібно додати їхні цифри першого розряду, потім цифри другого розряду і т.д. При цьому кожного ра­зу, коли при додаванні цифр даного розряду дістанемо суму більшу або рівну основі системи числення д, потрібно зробити перенесення одиниці в наступний розряд. Для зручності при виконанні додаван­ня чисел доданки доцільно підписувати один під одним (у стовпчик) так, щоб цифри, які відповідають однаковим розрядам, були одна

під одною. Як бачимо, додавання багатоцифрових чисел зводиться до додавання чисел одноцифрових. Основою додавання системних чисел є, таким чином, таблиця додавання одноцифрових чисел, що визначає суму двох чисел, менших, ніж основа д.

Можна показати, що віднімання, множення і ділення чисел вико­нується цілком аналогічно правилам звичайної шкільної десяткової арифметики.

Побудуємо, наприклад, таблиці додавання і множення одноци- фрових чисел в четвірковій системі числення:

+	0	1	2	3
0	0	1	2	3
1	1	2	3	10
2	2	3	10	11
3	3	10	11	12

	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	10	12
3	0	3	12	21

У кожній клітинці цих таблиць записано у четвірковій системі числення суму (добуток) чисел, що є номерами рядка і стовпця, на перетині яких стоїть дана клітинка. Користуючись цими таблицями і правилами, аналогічними правилам десяткової арифметики, вико­наємо арифметичні операції над числами в четвірковій системі чи­слення:

+203, 24 132,1₄ 1001,З4

_ 203, 2₄ 132,1₄

ЇГЇ

1024 214

1024 +2104

22024

2.4. Переведення цілих чисел з однієї позиційної систе­ми числення в іншу. У процесі розв'язування задач доводиться переводити цілі числа з однієї позиційної системи в іншу. Як же пе­ревести число а, записане в системі числення з основою 5, в систе­му числення з основою д? Як відомо, записати число а в системі числення з основою д - це означає зобразити його у вигляді суми а = «кд^к + ... + а₁ д + а₀. Отже, щоб записати число а в системі численя з основою д, треба знайти коефіціенти а₀, а₁,..., ак. Ці ко- ефіціенти знаходимо так. Поділимо в системі числення з основою 5

число а на д, дістанемо а = Ь₀ д + а₀. Далі поділимо Ь₀ на д, дістанемо Ь₀ = Ьі д + аі. Звідси

а = Ь₀ д + а₀ = (Ь_і д + а_і )д + а₀ = Ь_і д² + а_і д + а₀.

Потім поділимо Ь_і на д і т.д. Цей процес продовжуватимемо доти, поки не дістанемо частку, яка дорівнює нулю. Внаслідок цього мати­мемо:

_к

а = ак д + ... + аі д + а₀.

Оскільки за теоремою 2.3 число а можна подати у такому вигляді єдиним чином, то а₀, а_і,..., ак є цифрами числа а в системі числення з основою д.

Таким чином, для переведення натурального числа а, заданого в 8-ковій системі числення, в д-кову систему числення користуємось наступним правилом: спочатку записуємо число д в 8-ковій систе­мі, а потім виконуємо (в 8-ковій системі числення!) кілька ділень числа а₈ на число д₈ і послідовно утворюваних часток доти, по­ки дістанемо частку, яка дорівнює нулю. Здобуті остачі спочатку виражаємо цифрами д-кової системи числення і записуємо в зво­ротньому порядку. Записані таким чином остачі (це вже цифри в д-ковій системі ислення) і є д-ковим записом числа а₈.

4. Приклад. Запишемо число а = 47_і0 в трійковій системі числе­ння:

47= 15 • 3 + 2 15 = 5 • 3 + 0 5 = 1 • 3 + 2 1 = 0 • 3 + 1

Звідси випливає, що число а в трійковій системі числення запи­шеться а = 1202_з.

4. Приклад. Переведемо число а = 12210_з з трійкової системи числення у вісімкову. Нова основа у трійковій системі числення до­рівнює 22, тобто 8₈ = 22_з. Поділимо послідовно у трійковій системі числення число а = 12210_з на 22₃

12210₃ = 201з • 22з + 11з 201з = 2з • 22з + 10з 2з = 0з • 22з + 2з

Результати послідовного ділення записані у трійковій системі чи­слення, але ми знаємо, що 11₃ = 4₈ і 10₃ = 3₈. Отже, а = 234₈.

Перехід від д-кової системи числення до десяткової виконують ще й так. Число а_д записують у вигляді

ад = а_п д^п + ... + аі д + а₀.

Потім замість чисел а_п,... ,а_і,а₀ і д підставляють їхні десяткові за­писи і роблять відповідні обчислення. Десятковий запис результату є шуканим числом.

У випадку, коли д = 8^к перехід від однієї системи числення до іншої значно спрощується. Дійсно, нехай маємо два записи числа а в д-ковій і 8-ковій системах числення:

а = (ап ... аі ао )д = (Ьі... Ьі Ьо )8, тобто

а = ап д^п + ... + аі д + ао = Ьі 8^і + ... + Ьі 8 + Ьо. Покажемо спочатку, що для довільних с_о, с_і,... ,ск_—і, 0 < с_і < 8

(2) с_к—і8^{к і} + ... + Сі8 + Со <д.

Дійсно,

ск — і8^{к — і} + . . . + сі8+со < (8 —1)8^{к —і} + . . . + (8 —1)8 + (8 —1) = 8^к — 1 < 8^к = д.

З огляду на (2) остача а_о від ділення числа а = Ьі8^і + ... + Ьк8^к + Ьк—і8^к—і+.. .+Ьі8+Ьо = (Ьі8^і—к+.. .+Ьк)8^к+(Ьк—і8^к—і+.. .+Ьі8+Ьо) на д = 8^к дорівнює Ьк—і8^к—і +... + Ьі 8 + Ьо. Отже, (ао )д = (Ьк—і... Ьі Ьо )8. Далі, з рівності

ап д^п—і + ... + а2 д + аі = Ьі 8^і—к + ... + Ьк+і 8 + Ьк.

_к

неповних часток від ділення а на д = 8^к виливає, що

^(аі⁾д = ^(Ь2к —і . . . ^Ьк + і ^Ьк ⁾ 8.

Аналогічно можна одержати зобрження решти д-кових цифр в вигля­ді к-розрядних 8-кових чисел. Таким чином, для переведення числа, записаного в д-ковій системі числення, в 8-кову систему числення до­статньо кожну д-кову цифру замінити рівним їй к-розрядним 8-ковим числом.

4. Приклад. Переведемо число а = 765,163₈ в двійкову систему числення:

а = 765,163₈ = 1^11^101,, _ч0С)_^_ч11С^_ч011_> = 111110101,001110011₂.

7 6 5 1 6 3

Для переведення числа з двійкової в вісімкову систему числення достатньо розбити його праворуч і ліворуч від коми на тріади і за­мінити кожну тріаду відповідною їй вісімковою цифрою. Якщо при розбитті крайні тріади виявляться неповними, то їх слід доповнити нулями.

4. Приклад. Переведемо число а = 1011,1₂ в вісімкову систему числення:

а = 1011,12 = 0(Л 011,, ,100 = 13, 48.

13 4

Розглянемо метод переведення правильних дробів з однієї систе-

• Т Т" м м • /■* м • м

ми числення в іншу. Нехай правильний дріб а, заданий в 5-ковій системі числення, потрібно записати в системі численні з основою д. Припустимо, що запис числа а в д-ковій системі числення знайдений:

а = (0, а-іа-2 ... а-т)д = а-ід^-1 + а-2д^-2 + ... + а-тд^-т.

Якщо помножити число а на основу д нової системи числення, то ціла частина добутку буде дорівнювати а_{- 1} , а дробова -

а1 = а-2 д^-1 + ... + а-т д^-т+1.

Число а₁ є правильним дробом, оскільки всі цифри аі < д. Таким чином, в результаті множення числа а на д отримуємо цілу частину, яка дорівнює значенню цифри старшого розряду дробового д-кового числа. Продовуючи множення дробових частин а_і на основу д (цілі частини при кожному множенні відкидаються), можна одержати ре­шту цифр шуканого дробу: ними є цілі частини одержаних добутків. При цьому, якщо д < 5, то цілі частини добутку є цифрами д-кової системи числення, а якщо д > 5, то цілі частини є числами 5-кової системи числення, які необхідно замінити цифрами д-кової системи.

Сформулюємо правило переходу від однієї системи числення до іншої методом множення на основу: щоб перетворити правильний дріб з однієї системи числення в іншу, необхідно послідовно множи­ти це число і проміжні значення на основу нової системи числення (зображену в старій системі), відкидаючи кожен раз цілі части­ни добутків; ці цілі частини є зображенням цифр шуканого числа д-кової системи числення.

2.8. Приклад. Переведемо десяткове число а = 0, 6875ю в двійкову систему числення:

х0, 6875 2

X1, 3750 2

X 0, 7500 2

х 1, 5000 2

1,0000

Отже, а = 0,1011₂

Слід відмітити, що в загальному випадку дробові числа перево­дяться з однієї системи числення в іншу наближено, тобто дробова частина добутку при послідовному множенні на основу ніколи не до­рівнюватиме нулю. В цьому випадку процес множення продовжують доти, доки не буде одержана необхідна для досягнення заданої то­чності зображення числа кількість розрядів д-кового числа.

2.9. Приклад. Число 5 в десятковій системі числення записують скінченим дробом, а в дванадцятковій - нескінченним:

1=0,2ю = 0, 249724972497.. .12 ; 5

число 6, навпаки, в дванадцятковій системі числення записують скін­ченним дробом, а в десятковій - нескінченним:

11

- = 0, 2і2,- = 0,1666 ...10 . 66

В обох цих системах число 4 запишеться скінченним дробом, а число 1 - нескінченним:

1 = 0, 25ю = 0, З12,1 = 0,142857142857...10 = 0,186035186035 .. .12 .

Для переведення неправильного дробу з однієї системи числення в іншу слід цілу частину одержати методом ділення, а дробову - методом множення на основу нової системи числення.

Вправи до лекції 2.

2.1. Записати в десятковій системі числення такі числа римської нумерації: а) СXVI; б) СXIV; в) ^XСVI; г) МССИ; д) МС^XXIX; е) м^ссс^xxIV.

2. Записати в римській системі числення числа: а) 39; б) 93; в 2011; г) 1999.

3. Обчислити:

• (3333₄ + 2222₄) • 12₄;

• 20118 + 20128 - 43218;

• 206718/1318 - 1378;

• 120111_з/102_з + 201_з • 12_з - 11220_з;

• 2320115/104б + 12345 • 3225 - 10221315;

• 3215₇ • 24₇ - 11461₇/25₇ + 1532₇ - 115044₇.

2. Записати в десятковій системі числення такі числа:

а) 1000011012; г) 0, 221з;

б) 75634018; д) 11001,110012;

в) (10)7(11)9і2; е) 437,32018.

2. Перевести з однієї системи числення в іншу. Зробити перевірку.

а) 124ю ^ Х4; г) 320145 ^ Х8;

б) 1340_і0 ^ х_і4; д) 33311₇ ^ х_з;

в) 101000з ^ Х4; е) 34(11)57і2 ^ х_п.

2. Перевести з однієї системи числення в іншу.

а) 10111001101₂ ^ х₄; г) 1201222011,2111_з ^ х₉;

б) 13304 ^ Х2; д) 3387656,34559 ^ хз;

в) 1017658 ^ Х2; е) 1011100010101,12 ^ жіа.

2. Перевести число 2011, 2011₁₀ з десяткової системи числення в двійкову, трійкову та четвіркову системи числення.

3. а) 201х =418;

   б) 203х = 5310;

   в) 106_Ж = 153т;

   г) 236х = 12405;

   Знайти х, якщо:

д) 324х = 100223;

е) 364_ж = 30014; є) 401_ж = 265т;

ж) 541_х = 2014₆.

2. Знайти частку від ділення числа (62ху427)₁₀ на 99₁₀, а також невідомі цифри х і у, якщо ділення виконується без остачі.

3. Знайти таке найменше натуральне число т, яке в десятковій системі числення закінчується цифрою 6, причому, якщо цю цифру записати на початку числа, то воно збільшиться в 4 рази.

4. Число (42х4у)₁₀ дільться на 72₁₀. Знайти цифри х і у.

5. Нехай 2 • (хуг)₁₀ = (хуг)_д. Знайти (хуг)₁₀ і д.

Лекція 3. Регулярні мови і регулярні вирази

В цьому параграфі ми опишемо важливий клас формальних мов - регулярні мови і їх запис з допомогою регулярних виразів. Розгля­немо алгебраїчні закони для регулярних виразів. Ці закони багато в чому подібні до алгебраїчних законів арифметики, проте між ал­гебрами арифметичних і регулярних виразів є і суттєві відмінності. Регулярні вирази тісно пов'язані зі скінченними автоматами, які ми розглядатимемо в наступному розділі. їх можна також розглядати як "мову програмування" для опису деяких важливих додатків, на­приклад, програм текстового пошуку чи компонентів компілятора.

Нехай X - довільний алфавіт. Визначимо регулярну мову (мно­жину) в алфавіті X рекурсивно наступним чином:

1. порожня множина 0 є регулярною мовою;

2. для кожної букви а Є X множина {а} є регулярною мовою;

3. якщо А і В є регулярними мовами, то множини А ЦІ В, АВ і А* також є регулярними мовами;

4. інших регулярних мов не існує.

1. Приклад.

   1. множина {е} є регулярною мовою, бо {е} = 0*;

   2. множина {001,110} - регулярна мова над бінарним алфавітом, бо {001,110} = ({0}{0}{1}) У ({1}{1}{0});

   3. аналогічно, як і в пункті 2) , можна показати, що будь-яка скінченна мова є регулярною мовою.

Щоб спростити зображення регулярних мов, визначимо поняття регулярного виразу над алфавітом X наступним чином:

1. порожня множина 0 є регулярним виразом, який позначає порожню множину;

2. е є регулярним виразом, який позначає мову {е};

3. для кожної букви а Є X а - регулярний вираз, що позначає мову {а};

4. якщо га і те є регулярними виразами, що позначають мови А і В відповідно, то (га) + (гв), (га)(г_в ) і (га)* є регулярними виразами, що позначають мови А У В, АВ і А^* відповідно;

5. інших регулярних виразів над алфавітом X не існує.

Щоб зменшити кількість дужок в регулярних виразах, будемо вважати, що найвищий пріоритет має операція ітерації *, потім - конкатенація і останньою виконується операція +. Наприклад, 01 позначає {01}, 0* - {0}*, (0 + 1)* - {0,1}*, а (0 + 1)*001 позначає множину всіх слів, які складаються з нулів і одиниць і закінчуються словом 001.

Зрозуміло, що для кожної регулярної мови можна знайти при- наймі один регулярний вираз, який її зображує. I навпаки, для ко­жного регулярного виразу можна побудувати регулярну мову, що позначається цим виразом. На жаль, для кожної регулярної мови існує нескінченно багато виразів, що її зображують. Наприклад, ви­рази 0* 1 + 0 і 0* 1 зображують одну й ту ж мову {0}*{1}. Кажемо, що два регулярних вирази рівні (=), якщо вони позначають одну і ту ж множину.

2. Твердження. Нехай а, в і 7 - регулярні вирази. Тоді:

• а + в = в + а;

• 0* = е;

• а + (в + 7) = (а + в) + 7;

• ^а(в7⁾ = ^{(ав )}7;

• а(в + 7) = ав + а7;

• (а + в )7 = «7 + в7;

• ае = еа = а;

• 0а = а0 = 0;

• а* = а + а*;

• (а* )* = а*;

• а + а = а;

• а + 0 = а.

Доведення. Нехай а і в позначають множини А і В відповідно. Тоді а + в позначає А У В, а в + а позначає В У А. Але А У В = В У А за означенням об'єднання, тому а + в = в + а. Решту рівностей доводяться аналогічно. □

Для зручності запису введемо таке позначення: г+ = гг*.

Розглянемо деякі приклади.

2. Приклад. Довести рівності:

а) а*(а + 6)* = (а + 6а*)*;

б) (6а)+(а*6* + а*) = (6а)*6а+ 6*.

а) Покажемо, що обидві частини рівності дорівнюють (а + 6)*. Дійсно, обидві частини рівності є підмножинами (а + 6)*, оскільки (а + 6)* позначає множину всіх слів в алфавіті {а, 6}. Таким чином, достатньо показати, що обидві частини містять (а + 6)*. Оскільки е Є а*, то а* (а + 6)* ІЗ (а + 6)*. З того, що 6 Є 6а* випливає потрібне включення (а + 6)* С (а + 6а*)*.

б) (6а)+(а*6* + а*)=(6а)*(6а)а*(6* + е)=(6а)*6а+ 6*.

2. Приклад. Знайти регулярний вираз для множини всіх слів в ал­фавіті {0,1, 2}, які є записами в трійковій системі чисел натуральних степенів числа 9.

В трійковій системі числення степені 9^п запишуться як 1 00 „ . 0.

2 п

Таким чином, шуканий регулярний вираз має вигляд 1(00)*.

2. Приклад. Записати регулярний вираз для множини всіх слів у двійковому алфавіті, які містять підслово 001.

Таке слово запишеться у вигляді а001в, де а і в - довільні слова в двійковому алфавіті. Таким чином, одержуємо шуканий регулярний вираз:

(0 + 1)* 001(0+1)*.

3.6. Приклад. Записати регулярний вираз для множини всіх слів у двійковому алфавіті, які не містять підслова 001 .

Якщо слово ш належить шуканій множині, то воно не містить підслова 00, за винятком того випадку, коли воно має суфікс 0^к для к > 2. Аналогічно як і у прикладі 1.2, можна показати, що множина слів, які не містять підслова 00 записується з допомогою регулярного виразу (01 + 1)*(е+0). Таким чином, множина всіх слів, які не містять підслова 001 зображується наступним регулярним виразом:

(01 + 1)* (е + 0 + 000*) = (01 + 1)* 0*.

Розглянемо рівняння х = ах + в, де а і в регулярні вирази в алфавіті X і х Є X .З твердження 1.4 випливає, що якщо ефа, то х = а*в - єдиний розв'язок рівняння. У випадку е Є а рівняння має безліч розв'язків, кожен з яких, очевидно, має вигляд а* (в Ь 7), де 7 - довільна (не обов'язково регулярна) мова. Використовуючи твердження 1.4, можна розв'язувати системи рівнянь з регулярними коефіціентами (методом, аналогічним методу Гауса для розв'язуван­ня систем лінійних рівнянь).

Регулярні вирази часто зображують поміченими орієнтованими графами, стрілки яких позначають буквами з алфавіту X Ь {е}. Для довільного регулярного виразу г, граф, що його зображує, утворює­ться наступним чином:

Спочатку малюємо дві спеціальні вершини, які називаються по­чатковою і кінцевою вершинами, і сполучаємо їх стрілкою, позначе­ною г:

О—

Далі, повторюємо наступні кроки, доки кожна позначка довіль­ної стрілки не міститиме символів +, • і *:

1) замінюємо кожну стрілку з позначкою / + д на дві паралельні стрілки з позначками / і д:

О ^;+^д о ^ (С^Т^^їО

д

2. замінюємо кожну стрілку з позначкою /д на додаткову вер­шину і дві стрілки з позначками / і д:

о—^о ^ о^с^о

2. замінюємо кожну стрілку з позначкою / * на додаткову вер­шину і на три стрілки з позначками е, / і е:

О—^О ^ О^Сь^О

О

/

Для регулярного виразу г позначимо через С(т) помічений орієн­тований граф, що його зображує. Очевидно, що кожна стрілка в С(т) має позначку з множини X ЦІ {е}. Кожному шляху в С(т) відповід­ає слово, яке одержується конкатенацією всіх букв, які позначають стрілки шляху. Слово х належить мові Ь(т) тоді і тільки тоді, коли існує шлях в С(т) з початкової вершини в кінцеву вершину, якому відповідає слово х. Кожна е-стрілка в О(г), яка є єдиною вихідною стрілкою з некінцевої вершини чи єдиною вхідною стрілкою в непо- чаткову вершину може бути стягнута в одну вершину.

3.7. Приклад. Побудуємо граф С(т) регулярного виразу

г = (11+0)* (00 + 1)*.

Зобразимо, крок за кроком, побудову даного графу:

(11 + 0)* (00+1)*

•О-

^ (11 + 0)* _ (00+1)* -'О ^о ^>

е

>

^ о 11+0 00+1

01

° ^ о

Є е е

>

V

11 00

0

гл

1

1

гл

0

О

е

е

е

е

О

Стягнувши, де це можливо, е-стрілки, остаточно одержуємо по­мічений граф С(т) регулярного виразу г = (11 + 0)*(00 + 1)*:

1

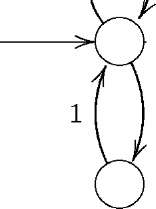
0

О

1

е

о 0 0

Вправи до лекції 3.

3.1. Знайти слово найменшої довжини в кожній з наступних регу­лярних мов. Які непорожні слова є найкоротшими в даних мовах?

а) 10+ (0 + 11)0* 1;

б) (00 + 11 + (01 + 10)(00 + 11)*(01 + 10))*; в) ((00+ 11)* + (001 + 110)*)*.

3.2. Визначити, чи належить рядок 1011 регулярним мовам:

г) (10) +1011;

д) 1(00)*(11)*;

а) 10*1;

б) 1(01)*1*; в) (10)+11.

е) (1+ 00)(01+ 0)1*.

3.3. Спростити наступні регулярні вирази:

а) (00)*0+(00)*;

б) (0 + 1)(е + 00)+ + (0+1);

в) (0 + е)0* 1.

3.4. Побудувати регулярні вирази для наступних мов в алфавіті

{0,1}:

а) Множина всіх слів, в яких п'ята буква справа є 0.

б) Множина всіх слів, які містять підслово 000 або 111.

в) Множина всіх слів, які не містять ні підслова 000, ні 111.

г) Множина всіх слів, які містять не більше однієї пари послі­довних одиниць.

д) Множина всіх слів, в яких кількість нулів кратна п'яти.

е) Множина всіх слів, які містять непарну кількість букв 0.

є) Множина всіх слів, в яких кількість одиниць ділиться на п'ять, а кількість нулів парна.

ж) Множина всіх слів, які містять непарну кількість входжень підслова 011. [Підказка: Спершу побудуйте регулярний вираз для множини бінарних слів, які не містять підслова 011.]

5. Визначити алфавіт та побудувати регулярний вираз для на­ступних мов:

а) Множина всіх непарних натуральних чисел, записаних в че- твірковій системі численя.

б) Множина всіх непарних натуральних чисел, записаних в трій- ковій системі численя.

5. Доведіть рівність (0² + 0^з)* = (0²0*)*.

6. Побудувати помічений граф для наступних регулярних вира-

зів:

а) 01 + 11*;

б) (00+10)(101)* +01;

в) ((00+11)* + (001 + 110)*)*;

г) а*Ь(с + ^а*Ь)*;

д) (а + Ьс*Ьс*.