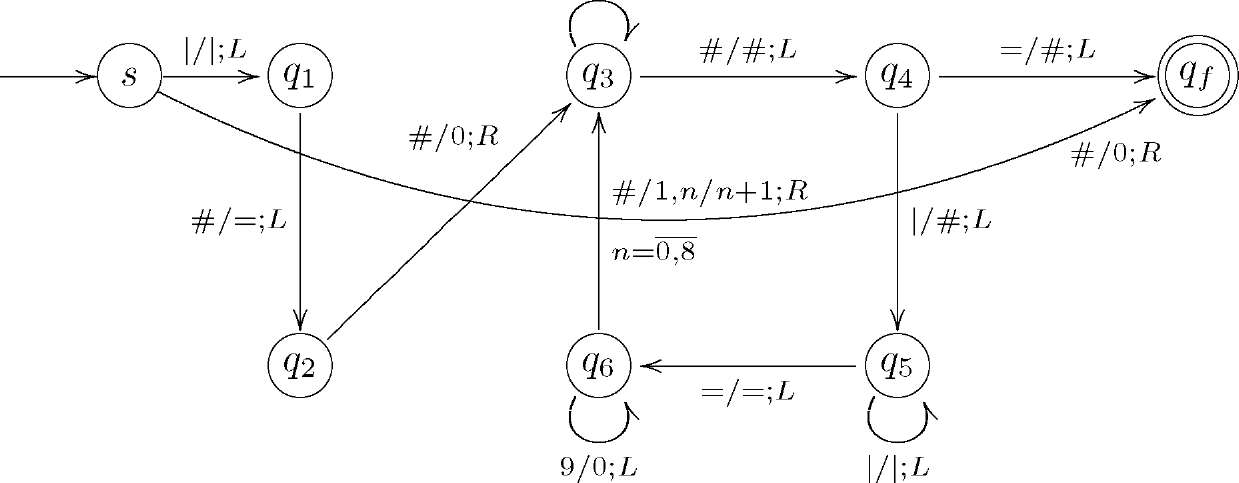
3.7. Приклад. Побудуємо машину Тюрінґа, яка переводить нату­ральні числа з унарної системи числення в десяткову.

Ідея розв'язання задачі така. Спершу зліва від унарного запи­су числа, перебуваючи в конфігурації (5, | ... |), в станах д₁ і д₂ до­писуємо допоміжний знак " = " і цифру 0 та переходимо в стан д_з. В результаті цього отримуємо конфігурацію (д_з, 0=| ... |). Далі, від унарного числа, розміщеного праворуч, віднімаємо одиницю (вити­раємо одну паличку) в стані д₄, переміщуємося ліворуч та в стані до десяткового числа додаємо одиницю, діючи за правилами десятко­вої арифметики. Після цього знову повертаємося до унарного числа праворуч і повторюємо циклічно всі операції доти, доки всі палички не будуть витерті. Наостанок, востаннє зсуваємося праворуч, в стані витираємо знак " = " і зупиняємося. Граф МТ матиме вигляд:

п/п,=/ = ,|/|; П, п=0,9

3.1. Композиція МТ. Нехай маємо дві машини Тюрінґа МТ₁ = ($1 ,А1 = X1 Ц У1 Ц Б1,51 ,з0,зп) і МТ2 = (^,А2 = X2 Ц У2 Ц Р₂, 5₂, д₀, д_т), причому вважаємо, що вихідний алфавіт першої маши­ни співпадає з вхідним алфавітом другої, тобто У₁ = X₂. Нехай ці МТ обчислюють словесні функції /₁ : )* ^ (У₁ )* та /₂ : (X₂)* ^ (У₂)* відповідно. Побудуємо МТ, яка обчислює їх композицію /₂ о /₁. На­гадаємо, що композицією функцій /₁ та /₂ називають таку функцію / = /₂ о /₁, що для кожного х з області визначення функіції /₁ зна­чення /(х) = /₂ (/1 (х)). При цьому вимагається, щоб функція /₂ була визначена на значенні /₁ (х) .

Машина Тюрінґа МТ = (Я, А = X Ц У Ц Б, 5, з, ) для функції / = /₂ о /₁ будується наступним чином. Вразі потреби, стани машини МТ₂ перепозначаємо так, щоб вони відрізнялися від станів машини МТ₁. Вхідний алфавіт X співпадає із вхідним алфавітом X₁ машини МТ₁, вихідний алфавіт У - з вихідним алфавітом У₂ машини МТ₂, а допоміжний алфавіт Б = X₂ Ц Б₁ Ц Б₂. Початковим станом МТ є початковий стан з₀ машини МТ₁, а кінцевим - кінцевий д_т машини МТ₂. Програми роботи 5₁ і 5₂ об'єднуємо і записуємо в одну таблицю. Доозначивши, що в стані з_п шукана МТ переміщується ліворуч до початку слова і потім переходить в стан д₀.

Нехай ш Є (X;!)* і розглянемо початкову конфігурацію (з,ш). Оскільки з = з₀, то на початку роботи МТ працює так як МТ₁ і якщо МТ₁ застосовна до слова ш, то на деякому кроці буде одер­жана конфігурація (з_п, /₁ (ш)). Далі, в стані з_п головка машини МТ

переміститься ліворуч під першу букву слова /і (ш) і керуючий при­стрій перейде в стан д₀, тобто одержимо конфігурацію (д₀, /_і(ш)). Якщо МТ₂ застосовна до слова /_і (ш), то на деякому кроці отримає­мо конфігурацію (д_т, /₂(/_і(ш))), яка є заключною для МТ, оскільки Яї = Я_т. Таким чином, якщо МТ_і застосовна до ш і МТ₂ застосовна до /і (ш), то і МТ застосовна до ш. Машина МТ називається компо­зицією машин МТ_і та МТ₂ і позначається через МТ₂ о МТ_і.

Означення композиції залишаються без змін, якщо МТ_і та МТ₂ обчислюють функції кількох змінних. Важливо лише, щоб дані для МТ₂ були у зумовленому вигляді підготовлені машиною МТ_і.

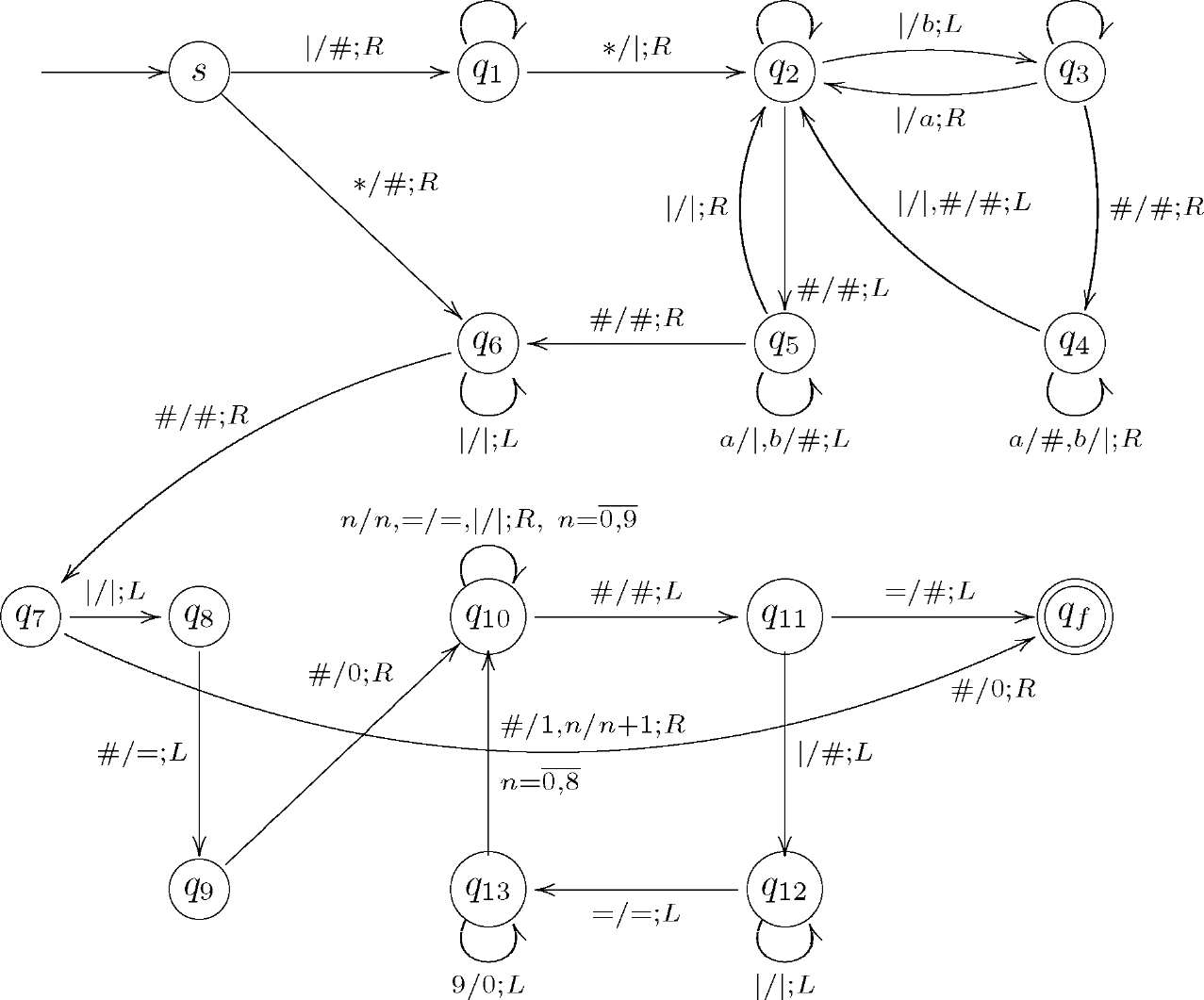
3.8. Приклад. Побудуємо МТ, яка обчислює функцію / : N0 х N ^ N /(п,т) = НСД(п, т) і видає результат в десятковій системі чи­слення.

Шукана МТ є композицією МТ, побудованих в прикладах 3.6 та 3.7. її граф має наступний вигляд.

|/|;Д а/а,Ь/Ь;Д а/а,Ь/Ь;Ь

3.2. Теза Тюрінґа-Черча. Аналізуючи попередні приклади, у читача складається враження, що процес, який відбувається на МТ, є сповільненим переглядом процесу обчислення, який виконується людиною відповідно до деякого алгоритму. Разом з тим, розглянуті приклади наштовхують на думку, що з допомогою МТ можна зада­вати і інші відомі нам алгоритми. Природньо виникає питання: чи спосіб задання алгоритмів з допомогою МТ є універсальним в тому сенсі, що будь-який алгоритм можна подати таким чином? На це пи­тання сучасна теорія алгоритмів дає відповідь з допомогою наступної гіпотези:

Теза Тюрінґа-Черча. Будь-який алгоритм можна реалізува­ти на відповідній машині Тюрінґа.

Перш за все, звернемо увагу на наступну характерну особливість даної гіпотези. В її формулюванні мова йде, з одного боку, про за­гальне поняття алгоритму, яке не є точним математичним поняттям; з другого боку, в цьому ж формулюванні мова йде про таке точне математичне поняття як машина Тюрінґа. Тому не може йти і мови про доведення даної гіпотези подібно до того як доводяться теореми в математиці. Значення гіпотези полягає саме в тому, що вона уто­чнює загальне, але розпливчасте поняття "будь-якого алгоритму" з допомогою цілком точного математичного поняття МТ. Таким чи­ном, теорія алгоритмів оголошує об'єктом своїх досліджень машини Тюрінґа. Тепер вже стають коректними питання можливості чи не­можливості побудови алгоритму для задачі того чи іншого типу.

Справидливість гіпотези підтверджується практикою, яка, як ві­домо з філософії, є єдиним критерієм істини. Всі відомі алгоритми, які були придумані впродовж багатьох тисячоліть історії математи­ки, можуть бути задані з допомогою МТ.

Вправи до лекції 3.

1. Побудувати машину Тюрінґа, яка обчислює числову функцію / : N0 — N0, аргументи якої задані в трійковій системі числення.

б) /(х) = 0;

₎ /_{( )} /0, х = 0

а) /(х) = <

|1, х = 0;

б) /(х) = х + 2;

в) /(х) = х - 2;

г) /(х) = 2 • х +1;

д) /(х) = 9ю • х + 2.

2. Побудувати машину Тюрінґа, яка обчислює числову функцію Р⁴ : (Ж₀)⁴ — N0, Р⁴(х₁ ,х₂,х_з,х₄) = хі, де і = 1, 2, 3, 4 (вважаємо, що аргументи хк задані в унарній системі числення).

3.3. Побудувати машину Тюрінґа, яка обчислює частково визначе­ну числову функцію / : (N0 )² — N0, аргументи якої задані в унарній системі числення.

ч ,/ ч /^{х -} ^ ^х > У ^{а) /(х,}У⁾ = <_п ,

^{0 х} < у;

б) /ху)= ^{х —у}

^{в) /(х,}у⁾ = ^хУ;

^{г) /(х,}У⁾ = тіп(^х,у};

д^{) /(х,}У⁾ = тах(^х,у^};

^{е) /(х,}у⁾ = [§1;

^{є) /(х,}У⁾ = ^{х -}у^[X].

4. Побудувати машину Тюрінґа, яка обчислює частково визначе­ну числову функцію / : N0 ^ N0, аргументи якої задані в унарній системі числення.

IX, х - парне

^{а) /(х)} = < 2

І |, х — непарне;

б) /(х) = [§ 1.

4. Побудувати машину Тюрінґа, яка обчислює частково визначе­ну числову функцію / : (N0 )² ^ N0.

^{а) /(х,}у⁾ = ^х + у;

^{б) /(х,}у⁾ = ^{х —} у.

Важаємо, що аргумент х заданий в четвірковій системі числення, а у - в трійковій системі. Результат отримати в четвірковій системі числення.

4. Доведіть, що функція

І 1, якщо х ділиться на р

^/р ^(х) = <_п

І 0, якщо х не ділиться на р

обчислюється деякою МТ.

4. Побудувати машину Тюрінґа, яка обчислює словесну функцію / : {а,ЬУ ^{а,ЬУ.

а) /(ш) = шаЬ;

б) /(ш) = ш^н;

в) /(ш) = шш;

г) /(ш) = шш^н.

4. Побудувати машину Тюрінґа, яка переводить натуральні чи­сла з трійкової системи числення в унарну.

5. Побудувати машину Тюрінґа, яка переводить натуральні чи­сла з четвіркової системи числення в двійкову.

6. Побудувати машину Тюрінґа, яка переводить натуральні чи­сла з двійкової системи числення в четвіркову (підказка: врахуйте, що в двійковому числі може бути непарна кількість букв).

7. Скориставшись композицією МТ, побудуйте машину Тюрі­нґа, яка за записом числа в унарній системі числення визначає, чи є це число степенем 3 (1,3, 9, 27,...). Відповідь: 1 якщо так, 0 - в протилежному випадку.