2. Приклад. Застосувати кожну з підстановок з попереднього при­кладу до слова аЬЬасЬа максимальну можливу кількісить разів.

Застосувавши один раз підстановку аЬ ^ ас до слова аЬЬасЬа одержимо слово асЬасЬа, яке вже не містить підслова аЬ, а тому дана підстановка більше не застосовна. Підстановка з пункту б) не за­стосовна до слова аЬЬасЬа. Після першого застосування підстановки Ьа ^ до слова аЬЬасЬа отримуємо слово аЬсЬа, до якого ще раз мо­жна застосувати дану підстановку. Остаточно одержуємо слово аЬс, до якого вже не застосовна підстановка з пункту в). Оскільки під­становка Ь ^ с є заключною, то вона застосовується тільки раз до вхідного слова і її результатом є слово асЬасЬа.

Нормальним алгоритом Маркова називається пара (А,Р), де А - алфавіт, а Р - впорядкована скінченна послідовність формул під­становки:

01

а2

02

{а_к — вк

яка називається схемою підстановок. При цьому вважається, що в Р виділено деяку підмножину Ру С Р заключних формул підстановки.

Роботу НАМ можна описати наступним чином. Нехай задано де­яке вхідне слово ш (в НАМ не важливо, де саме воно записано). Далі, всі формули схеми підстановок проглядаються зверху вниз, обирає­ться перша з формул, яка застосовна до слова ш, і виконується під­становка відповідно до знайденої формули підстановки. В результаті одержується нове слово V. Потім ті ж самі дії виконуються з словом V і т.д. При цьому зауважимо, що на кожному кроці формули в Р завжди проглядаються зверху вниз, починаючи з першої формули! Якщо на черговому кроці була застосована звичайна формула під­становки, то робота НАМ продовжується, якщо ж - заключна фор­мула, то після її застосування робота НАМ зупиняється і одержане слово називається вихідним словом або результатом застосування НАМ до вхідного слова ш. У випадку, якщо на деякому кроці жо­дна з формул схеми Р не застосовна до проміжного слова, то робота НАМ також зупиняється і вихідним словом вважається дане промі­жне слово. В обох розглянутих останніх випадках кажуть, що НАМ застосовний до вхідного слова ш.

5.3. Приклад. Застосувати кожен з нам

аЬ Ьа

Ьа

Ьа аЬ

б)

а

Ьа

в алфавіті А = {а, Ь} до слова аЬЬЬЬаа.

а) Спершу застосовуємо першу підстановку максимально можли­ву кількість разів: аЬЬЬЬаа ^ ЬаЬЬЬаа ^ ЬЬаЬЬаа ^ ЬЬЬаЬаа ^ ЬЬЬЬааа. Потім застосуємо до слова ЬЬЬЬааа підстановку Ьа — : ЬЬЬЬааа ^ ЬЬЬаа ^ ЬЬа ^ Ь. В результаті одержуємо слово Ь. Оскільки жодна з

формул схеми а) не застосовна до слова Ь, то НАМ застосовний до слова аЬЬЬЬаа.

б) Застосуємо НАМ до слова аЬЬЬЬаа: аЬЬЬЬаа ^ аЬЬЬа ^ аЬЬ ^ ЬаЬ. Оскільки ми використали заключну підстановку аЬ ^ Ьа, то робота НАМ зупиняється і алгоритм з пункту б) застосовний до слова аЬЬЬЬаа.

Однак, може трапитися так, що НАМ ніколи не зупиниться, тоб­то на кожному кроці до проміжного слова застосовна звичайна фор­мула. В цьому випадку кажуть, що НАМ не застосовний до вхідного слова ш або зациклюється на вхідному слові ш. Область застосува­ння НАМ - це множина всіх слів, до яких застосовний даний НАМ.

4. Приклад. Визначимо область застосування НАМ відносно ал­фавіту А = {а, Ь}:

а ^ а Ь ^ а

Перша формула застосовна до будь якого вхідного слова, яке мі- ститить хоча б одну букву а, причому вона не змінює даного слова. Тому на таких словах НАМ зациклюється. Якщо ж у вхідному слові немає букв а, але є хоча б одна буква Ь, тоді перша формула не буде застосовуватися, а відразу виконується друга підстановка і НАМ зу­пинить свою роботу. До порожнього вхідного слова жодна з формул підстановок не застосовна, а тому НАМ до нього застосовний. Отже, область застосування даного НАМ - всі слова Ь^п (п > 0).

4. Приклад. Побудуємо НАМ, який застосовний до всіх слів в алфавіті А = {а, Ь}, крім слів аа та аЬ.

З умови задачі випливає, що НАМ має зациклюватися на словах аа та аЬ. Однак алгоритм

аа ^ аа аЬ ^ аЬ

не є розв'язком даної задачі, оскільки він зациклюється не тільки на даних словах, але й на будь яких інших словах, які містять підслово аа або аЬ. Зазвичай задачі такого типу розв'язують наступним чином: початок і кінець вхідного слова ш відмічають спеціальними мітками (наприклад, ¹ш^), а потім використовують формули підстановки, в

•а - •Ь - *аа« *аЬ«

* і—>

а«

ь

*аа«

аь

Два НАМ над одним і тим же алфавітом А називаються рівно­сильними, якщо їх області застосувань співпадають і на однакових вхідних словах вони видають однакові результати.

5.6. Приклад. Визначити, чи еквівалентні наступні пари НАМ від­носно алфавіту А = {а, Ь}:

: {

Р2

ЬЬ Ьа

а) Р1 : ІЬЬ — аЬ

аЬ ааЬ

Ь

Ьа

а Ь

а Ь

б) Рз :

Рд :

: {

в) Р

Ь Ьа

а Ь

а^

Ьа

Рб :

Розглянемо схеми Р₁ і Р₂ НАМ з пункту а). У них одна і та ж область застосування - множина всіх слів в алфавіті А = {а, Ь}. Однак друга умова рівносильності (однакові результати на однако­вих вхідних словах) не виконується. Дійсно,

Р₁ : аЬЬЬ ^ ааЬЬ ^ аааЬ, Р₂ : аЬЬЬ ^ аЬаЬ.

Отже, НАМ з пункту а) не рівносильні.

У НАМ Р_з і Р_д області застосування співпадають і містять тіль­ки єдине слово - порожнє. На непорожніх словах дані алгоритми зациклюються, причому зациклюються по-різному. Однак така рі­зна поведінка при зациклюванні не відіграє жодної ролі в означенні

рівносильності алгоритмів. Важливо тільки, щоб у випадку зупинки алгоритми видавали однакові вихідні слова. А для пари з пункту б) ця умова виконується: на єдиному слові (порожньому), до якого во­ни застосовні, НАМ видають одну і ту ж відповідь - порожнє слово. Таким чином, дані алгоритми рівносильні.

В алгоритмів з пункту в), які замінюють перше входження букви Ь на Ьа, не співпадають області застосування: Р₅ застосовний до всіх слів в алфавіті А, а Р₆ зациклюється на словах, які не містять букви Ь. Отже, алгоритми з пункту в) не рівносильні.

Вправи до лекції 5.

1. Нормальний алгоритм Маркова ({а, Ь},Р) задається схемою

' Ьа ^ а ЬЬ ^ Ь . аЬ ^ ^ Ь

V

Р : <

Застосуйте його до слів ЬЬаЬ, ааааЬ, ЬЬааЬЬа.

2. а Ь

   В чому полягає робота НАМ (А,Р), де А = {а, Ь}, а схема Р

має вигляд:

Р:

ЬаЬа

5.3. Визначити область застосування НАМ з алфавітом А = {0,1, 2}, якщо:

а) Рі

б) Р2

2 ^ 2 0

22 ^ 2 000 00

1 ^ 0 2 ^ 1 00 ^ 00

2 ^ 1 1 ^ 0 00 ^ 00

в) Рз :

Рл : <

5.4. Знайти область застосування та визначити в чому полягає ро­бота НАМ ({а,Ь},Р), де

а — аа Р : ІЬЬ

Р:

Ь і—> аЬ

5.5. Побудувати НАМ в алфавіті А = {0,1}, який застосовний тіль­ки до порожнього слова та слова 1000.

5.6. Зі схеми

1 — 0 01 — 111 01

викреслити рівно одну формулу підстановки, щоб одержати НАМ, який застосовний до всіх слів в алфавіті А = {0, 1}.

5.7. Для кожної пари НАМ визначити чи рівносильні вони відносно алфавіту {0, 1}:

: {

1

11 1

11

Р2 :

а) Р1

10 — 01 01

01 10

б) Р3 :

Р4 :

Г ^0 — 0«

•1 — •—

11

• 1 •0

★1 ★0

* ь

1* 0

Рб :

в) Р5 :

5.8. З НАМ в алфавіті {0,1}, заданого схемою

Г 010 — 001 10 — 01 0101 — 0011 01

викреслити якомога більше формул підстановки так, щоб одержаний алгоритм був рівносильний даному.

Р : <

5.9. Побудувати машину Тюрінґа, яка рівносильна вказаному НАМ в алфавіті {0,1}:

.1 — 0«

а) Р : < .0 0

01 — 01 б) Р : <(10 — 10

—>

5.10. Проаналізувати роботу нормального алгоритму Маркова, за­даного над алфавітом А = {а\, а₂,..., а_т} зі схемою

** — #

#а — а#, де а Є А

Р : ^— #

# —

*аЬ — Ь * а, де а,Ь Є А

*

Лекція 6. Синтез нормальних алгортмів Мар­кова

Розглядаються задачі на складання нормальних алгоритмів Мар­кова, на прикладах пояснюються основні прийоми складання таких алгоритмів.

6.1. Приклад. Побудувати НАМ, який застосовний до всіх слів в алфавіті А = {а, Ь, с} і видаляє із вхідного слова перше входження букви а (якщо таке є), а букви Ь замінює на с.

Перш за все відмітимо, що в НАМ, на відміну від машини Тюрі­нґа, легко реалізуються вставки, заміни та видалення букв. Напри­клад, заміна букви ь на букву с здійснюється за допомогою формули підстановки Ь ^ с, а видалення букви а реалізується формулою а При цьому проміжне слово розтягується або стискається автомати­чно. В шуканому алгоритмі спершу всі букви Ь мають замінюватися на с, тому першою формулою має бути Ь ^ с. Далі, коли букв Ь у слові вже не залишиться, маємо витерти першу букву а, для чо­го використовуємо заключну підстановку а Таким чином, НАМ матиме вигляд:

с

6.2. Приклад. Побудувати НАМ, який сортує непорожнє слово в алфавіті А = {0,1} (послідовність цифр 0 і 1) в порядку незростання.

Дана задача розв'язується з допомгою НАМ, який містить єди­ну формулу підстановки 01 ^ 10. Поки у слові праворуч від хоча б однієї цифри 0 є цифра 1, дана формула буде переносити 1 ліворуч від цього 0. Формула стає незастосовною, коли праворуч від 0 не­ма жодної 1, тобто коли вхідне слово відсортоване по незростанню. Наприклад,

0110 ^ 1010 ^ 1100.

6.3. Приклад. Побудувати НАМ, який застосовний до всіх слів в алфавіті А = {а, Ь} і видаляє останню букву вхідного слова.

Для розв'язання задачі потрібно якимось чином зафіксувати, по­мітити останню букву, наприклад, поставивши після неї новий спец- знак, скажімо *. Але як помістити цей знак вкінці слова? Робиться це наступним чином: спочатку * дописуємо ліворуч до вхідного слова, а потім "переганяємо" в його кінець. Неважко помітити, що "пере­скакування" зірочки через букву - це заміна пари *х на пару х*, яка здійснюється з допомогою формули підстановки *х ^ х*. Після то­го як * опиниться вкінці слова, потрібно витерти останню букву і * та зупинити роботу алгоритму. Таким чином, одержуємо наступний

НАМ:

^ *

*а ^ а* < *Ь ^ Ь* а* ^ Ь* ^

V

Проаналізуємо його роботу на слові аЬЬ:

аЬЬ ^ *аЬЬ ^ * * аЬЬ ^ * * *аЬЬ ^ ...

Бачимо, що цей алгоритм постійно дописує зліва зірочки. Чому? Нагадаємо, що формула підстановки з порожньою лівою частиною застосовна завжди, тому наша перша формула працюватиме нескін­ченно, блокуючи доступ до наступних формул. Звідси випливає дуже важливе правило: якщо в НАМ є формула з порожньою лівою ча­стиною, то вона має міститися вкінці НАМ. З урахуванням цього наш алгоритм перепишеться так:

ґ

*а ^ а* *Ь ^ Ь* < а* ^

Ь* ^ ^ *

V

Однак це ще не все: наш алгоритм зациклюється на порожньому вхідному слові, оскільки остання формула завжди буде застосовна. В чому причина помилки? Річ у тім, що ми ввели знак * для того, щоб помітити останню букву вхідного слова, а потім видалити * і цю букву. Щоб врахувати випадок порожнього слова, треба перед остан­ньою формулою записати ще одну формулу, яка видаляє "одиноку" зірочку і зупиняє алгоритм. Таким чином, остаточно НАМ матиме вигляд:

*а — а* *Ь — Ь* а* —

<

Ь* —

* і—> —> *

V

6.4. Приклад. Побудувати НАМ над алфавітом А = {а, Ь}, який подвоює кожне входження букви Ь та дописує вкінці слова суфікс ЬаЬа.

На перший погляд, щоб подвоїти кожну букву Ь, досить застосу­вати формулу Ь — ЬЬ. Щоб переконатися, що це не так, розглянемо приклад

ЬаЬ — ЬЬаЬ — ЬЬЬаЬ — ...

Помилка тут у тому, що після заміни першого входження букви Ь на ЬЬ ми не можемо відрізнити вже замінені букви Ь від тих, які ще не мінялися. Для вирішення цієї проблеми можна помітити зліва спецзнаком * ту букву Ь, яку потрібно в даний момент замінити, а пі­сля того як така заміна вже здійснена, спецзнак потрібно премістити до наступної букви.

Таким чином, потрібно спершу розмістити ліворуч від вхідного слова спецзнак *, а потім "перескакувати" через наступну букву, не змінюючи її, якщо ця буква а і подвоюючи, якщо це є Ь. Вкінці, коли праворуч від * вже не виявиться жодної букви, спецзнак потрібно поміняти на слово ЬаЬа.

Отже, отримуємо наступний НАМ:

' *а — а* *Ь — ЬЬ*

<

* — ЬаЬа —> *

V

Перевіримо його на вхідному слові ЬаЬ:

ЬаЬ —> *ЬаЬ —> ЬЬ* аЬ —> ЬЬа* Ь —> ЬЬаЬЬ* —> ЬЬаЬЬЬаЬа

6.5. Приклад. Побудувати НАМ над алфавітом А = {а, Ь}, який видаляє останнє входження букви Ь (якщо таке є).

Для того, щоб помістити * поруч з останнім входженням букви Ь, можна спершу перемістити * вкінець слова, а потім перенести * спра­ва наліво через букви а до найближчої букви Ь. При цьому потрібно врахувати, що вхідне слово може не містити букви Ь: якщо зірочка знову досягне початку слова, то її потрібно видалити і зупинитися. Реалізуємо дану ідею з допомогою наступного НАМ:

*а —	► а*
*Ь —	Ь*
а* —	► *а
Ь* —
* і—>
—> *

Перевіримо роботу даного алгоритму на вхідному слові аЬа:

аЬа — *аЬа ^ аЬа* — аЬ*а — аЬа* — ...

Як бачимо, замість того, щоб рухатися справа наліво до най­ближчої букви Ь, зірочка почала "кружляти" навколо останньої бу­кви слова. Чому? Річ у тім, що перші дві формули, які переміщують * праворуч, заважають третій формулі. Відмітимо, що переставлян­ня цих формул не приведе до потрібного результату, оскільки тоді * почне бігати навколо першої букви вхідного слова. Помилка полягає в тому, що ми використовуємо спецзнак * як для руху ліворуч, так і для руху праворуч. Щоб виправити цю помилку, потрібно просто ввести ще один спецзнак, наприклад поділивши між цими спец- знаками обовязки: нехай * переміщується праворуч, а # - ліворуч. З'явитися ж спецзнак # має тоді, коли * дійде до кінця слова, тобто коли справа від * не виявиться інших букв. Остаточно, отримаємо такий НАМ:

*а ^ а*

*Ь ^ ь* #

< а# ^ #а

Ь# ^ # ^

^ *

6. Приклад. Побудувати НАМ, який застосовний до всіх слів в алфавіті А = {а, Ь, с} і визначає скільки різних букв міститься у вхідному слові. Відповідь одержати в унарній системі числення (на­приклад: ааЬЬаЬ ^ ||).

Для розв'язання цієї задачі спочатку відсортуємо вхідне слово таким чином, щоб спершу були всі букви а, потім Ь, а вкінці букви с. Далі, видалимо так букви, щоб залишилась максимальна кількість попарно різних букв. Для цього скористаємось формулами підстанов­ки виду хх ^ х. Наостанок, замінимо всі букви на палички. Шуканий НАМ матиме вигляд:

' Ьа ^ аЬ са ^ ас сЬ ^ Ьс аа ^ а < ЬЬ ^ Ь сс ^ с а ^ |

Ь ^ | ,^с ^ ¹

Наприклад,

ааЬЬаЬ ^ ааЬаЬЬ ^ аааЬЬЬ ^ ааЬЬЬ ^ аЬЬЬ ^ аЬЬ ^ аЬ ^ | Ь ^ ||.

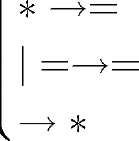
6. Приклад. Побудувати НАМ над алфавітом А = {0,1}, який дописує праворуч до вхідного слова (двійкового числа) знак " = "і стільки паличок, зі скількох цифр складається двійкове число.

Розв'яжемо дану задачу наступними чином. Спершу за кожною цифрою вхідного слова вставимо паличку |. Для цього допишемо злі­ва до вхідного слова спецзнак *, а потім перенесемо його через кожну цифру так, щоб зліва від нього залишалася ця цифра і відповідна їй паличка. В кінці слова замінюємо * на новий спецзнак =, який буде­мо використовувати далі:

10 ^ *10 ^ 1| * 0 ^ 1|0|* ^ 1|0| =

В одержаному слові переставляємо букви і палички так, щоб злі­ва опинилися всі букви, а справа палички, зберігаючи при цьому вихідний взаємний порядок як букв, так і паличок:

1|0|* ^ 1101 ... ^ 101| =

Залишилось премістити = ліворуч до першої букви.

Всі вказані дії описуються наступним алгоритмом Маркова:

'*1 ^ 1|* *0 ^ 0|* |0 ^ 0| 11

Вправи до лекції 6.

В задачах 6.1-6.21 побудувати НАМ, який застосовний до всіх слів в алфавіті А, і виконує наступну роботу.

1. А = {Н, П, У}. Дописати справа до вхідного слова ш слово ПНУ (ш ^ шПНУ).

2. А = {а,Ь}. Залишити в слові тільки першу букву (порожнє слово не міняє).

3. А = {а, Ь}. Залишити в слові тільки останню букву (порожнє слово не міняє).

4. А = {а, Ь, с}. За першою буквою непорожнього вхідного слова вставити букву с.

5. А = {а, Ь, с}. Якщо у вхідному слові є принаймі дві букви, то поміняти місцями перші дві букви.

6. А = {а, Ь}. Якщо вхідне слово містить більше букв а, ніж букв

   2. то видати вихідне слово з однієї букви а, якщо однакова кількість букв а і Ь, то видати порожнє слово, інакше видати слово Ь.

7. А = {а, Ь}. У вхідному слові всі букви а замінити на Ь, а всі (попередні) букви Ь - на а.

8. А = {а, Ь, с}. Подвоїти кожну букву у вхідному слові.

9. А = {а, Ь}. Дописати праворуч до вхідного слова стільки па­личок, зі скількох підряд записаних букв Ь починається це слово.

10. А = {а, Ь}. Зі всіх входжень букви а у вхідне слово залишити тільки останнє входження, якщо так є.

11. А = {а, Ь}. Якщо вхідне слово містить одночасно букви а і Ь, то замінити його на порожнє слово.

12. А = {а, Ь}. Якщо вхідне слово не є словом ааЬЬа, то замінити його на порожнє слово.

13. А = {а, Ь}. Визначити чи входить перша буква непорожнього вхідного слова ще раз у це слово. Відповідь: слово а, якщо входить, або порожнє слово в протилежному випадку.

14. А = {а, Ь}. Перенести останню букву непорожнього вхідного слова на його початок.

15. А = {а,Ь}. В непорожньому вхідному слові переставити мі­сцями першу та останню букви.

16. А = {а,Ь}. Якщо в непорожньому вхідному слові співпадають перша та остання букви, то видалити ці букви, в іншому випадку слово не змінювати.

17. А = {а, Ь, с}. Якщо вхідне слово не містить букви с, то замі­нити всі букви а на Ь. В іншому випадку видати слово з однієї букви

18. А = {а,Ь}. Подвоїти вхідне слово (дописати справа його ко­пію).

19. А = {а, Ь}. Обернути вхідне слово (наприклад, ааЬ — Ьаа).

20. А = {а, Ь}. Визначити чи є слово поліндромом. Відповідь: слово а, якщо є, або порожнє слово в протилежному випадку.

21. А = {а, Ь}. Нехай вхідне слово має непарну довжину. Вида­лити з нього середню букву.

Лекція 7. Нормально обчислювані функції. Ком­позиція НАМ

В даному параграфі ми розглядатимемо функції, для яких існує нормальний алгоритм Маркова, що їх обчислює. Відмітимо, що при аналізі деяких вхідних слів алгоритм Маркова може ніколи не зупи­ниться (зациклюється), і, отже функція може бути не визначена для деяких вхідних слів (аргументів). В загальному випадку, кажемо, що функція / : (X * )^п — У * є частково визначеною функцією, якщо во­на не визначена для деяких наборів аргументів (хі,..., х_п) Є (X*)^п, тобто коли область визначення / є підмножиною (X * )^п. Якщо обла­стю визначення / співпадає з (X*)^п, то кажемо, що функція / всю­ди визначена на (X*)^п. Якщо функція / не визначена на наборі (х_і,... ,х_п), то писатимемо /(х_і,... ,х_п) =|.

Кажемо, що частково визначена функція / : (X * )^п — У * є нор­мально обчислюваною, якщо існує такий нормальний алгоритм Мар­кова, що для кожного набору (х_і,..., х_п) Є (X*)^п, на якому / визна­чена, НАМ перетворює вхідне слово х_і * х₂ *... * х_п у вихідне слово у, де у = / (х_і,..., х_п) Є У *, а * - спеціальний допоміжний символ, який розділяє вхідні аргументи; і для кожного набору (х_і,..., х_п) Є (X* )^п, для якого функція не визначена НАМ зациклюється.

Надалі, найчастіше розглядатимемо числові функції / : (N0)^п — N0, де N0 = N ЦІ {0}.

7.1. Приклад. Покажемо, що функція / : N0 — N0, /(п) = 0 обчи­слюється з допомогою деякого НАМ.

Вважатимемо, що невід'ємні цілі числа записані в двійковій си­стемі числення. Для побудови НАМ, який правильно обчислює дану функцію, достатньо витерти всі букви (цифри 0 і 1) вхідного сло­ва, а потім написати 0 і зупинити роботу НАМ. Таким чином, НАМ матиме вигляд:

0 — 1 — — 0

Нагадаємо, що

п — т, п > т

т — п, п < т

7.2. Приклад. Покажемо, що функція / : N0 х N0 — N0, /(п,т) = |п — т| є нормально обчислюваною (вважаємо, що невід'ємні цілі числа записані в унарній системі числення).

|п — т| =

На початку роботи вхідне слово має вигляд || ... | * || ... |. Оскільки

пт

|п — т| = |(п — 1) — (т — 1)|, то для розв'язання задачі досить ви­тирати по одній паличці зліва і справа доти, доки в якісь частині не

залишиться жодної палички. Отже, НАМ задається схемою

* | —> *

* і—>

Наприклад, || * |||| — | * ||| — *|| — || і /(2, 4) = |2 — 4| =2.

7.3. Приклад. Покажемо, що функція / : N0 — N0, /(п) = п той 4, яка обчислює остачу від ділення натурального числа на 4, є нор­мально обчислюваною (вважаємо, що невід'ємні цілі числа записані в унарній системі числення).

Оскільки остачі від ділення чисел п і п — 4 на 4 одинакові, то для знаходження остачі досить від числа віднімати 4 доти, доки не отримаємо число менше 4 - воно і буде шуканою остачею. Таким чином НАМ буде наступним:

{|||| —

Наприклад, ||||||||| — ||||| — | і /(9) = 1.

4. Приклад. Покажемо, що функція / : N0 — N0, /(п) = [п/4], є нормально обчислюваною.

Для знаходження цілої частини від ділення числа п на 4, досить спершу підрахувати скільки четвірок паличок містить це унарне чи­сло, а потім витерти палички, які відповідають остачі. Дані мірку­вання реалізуються такою схемою НАМ:

' *ІІІІ — І* *| — *

<

* і—> —> *

V

Наприклад, /(9) = 1 і ||||||||| — *|||ШШ — |*||||| — ||*| — ||* — ||.

4. Приклад. Комбінуючи попередні два приклади, покажемо, що функція / : N0 — N0 х N0, /(п) = ([п/4],п той 4), є нормально обчислюваною.

Легко бачити, що дана задача розв'язується такою схемою НАМ:

*ІІІІ — І* *—*

*

7.6. Приклад. Побудуємо НАМ, який обислює функцію / : N — N /(п) = п + 2 (вважаємо, що натуральні числа задані в трійковій системі числення)

Для розв'язання задачі спрешу введемо спецзнак * і перемісти­мо його вкінець слова, щоб помітити його останню букву (трійкову цифру). Якщо цією цифрою є 0, то замінюємо її на 2 і зупиняємо роботу, інакше міняємо 1 на 0, 2 на 1 (додаємо двійку до останньої цифри) і переміщуємося ліворуч для додавання 1 до попередньої ци­фри з допомогою нового спецзнаку

Всі розглянуті дії описуються таким НАМ:

'*0 — 0*

*1 — 1* *2 — 2* 0* — 2 1* — #0

< 2* — #1 0# — 1 1# — 2 2# — #0

# — 1

—> *

7.7. Приклад. Нехай вхідний алфавіт А = {0,1, 2, 3}. Вважаючи вхідне слово записом числа в четвірковій системі числення, перевести це число в двійкову систему числення.

Як відомо, для переведення числа з четвіркової системи числе­ння в двійкову, потрібно кожну четвіркову цифру замінити на пару відповідних їй двійкових цифр: 0 — 00, 1 — 01, 2 — 10, 3 — 11, див. ??. Користуючись цим, схему НАМ запишемо так:

'*0 — 00* *1 — 01* *2 — 10*

<

*3 — 11*

* і—> —> *

7.1. Композиція НАМ. Нехай маємо два нормальні алгори­тми Маркова НАМі і НАМ₂ в одному і тому ж алфавіті А. Нехай ці НАМ обчислюють словесні функції /₁ : А* — А* та /₂ : А* — А* відповідно. Нас цікавитимуть НАМ, які обчислюють їх композицію /₂ ◦ /₁. Нагадаємо, що композицією функцій /₁ та /₂ називають таку функцію / = /₂ о /і, що для кожного х з області визначення функції /і значення /(х) = /₂ (/і (х)). При цьому вимагається, щоб функція /₂

була визначена на значенні /_і (х). Якщо вихідне слово НАМ і подати на вхід НАМ ₂, то таке послідовне виконання цих алгоритмів нази­вається композицією НАМ_і та НАМ₂ і позначається НАМ₂ (НАМ_і). При цьому треба враховувати, що якщо будь-який з алгоритмів за­циклюється, то зациклюватися має і їх композиція.

Доведена наступна теорема: для будь-яких двох нормальних ал­

А"

та

горитмів в алфавіті А, які обчислюють функції /_і : А*

/₂ : А* — А* відповідно, існує НАМ, який обчислює композицію

^/2 ◦ ^/і ^, д^ив. [?]

7.8. Приклад. Побудуємо нормальний алгоритм, який є компози­цією наступних двох алгоритмів НАМ_і і НАМ₂ відносно алфавіту {а^,ь}:

: {

Р2

ь

*а

*ь

* I-

а* аЬ*

>

Рі

Спершу відмітимо, що в загальному випадку не можна будувати композицію простим виписуванням одна за одною формул підстанов­ки з НАМ_і і НАМ₂. Наприклад, якщо спочатку виписати формули з НАМ_і, а потім з НАМ₂, то отримаємо алгоритм НАМ_і2, а якщо спершу випсати формули з НАМ₂, а потім з НАМ_і, то отримаємо алгоритм НАМ_2і, які задані схемами

Ь - *а

*ь

* I-

*а

*ь

* I-

а* аЬ*

а* аЬ*

^Рі

Р2

і2

2і

Але ні НАМ_і2, ні НАМ_2і не є композицією алгоритмів НАМ_і і НАМ₂. Наприклад, для вхідного слова ааа маємо:

Р_і2 : аЬа — *аЬа — а * Ьа — ааЬ * а — ааЬа* — ааЬа

^Р2

2і

аЬа —> аа —> *аа —> а* а —> аа* —> аа,

тоді як НАМ₂ (НАМі (аЬа))=НАМ₂(ааЬа) = ааа.

Відмітимо, що існує загальний метод побудови композизії НАМ, див. [?]. Однак цей спосіб досить громіздкий і для простіших НАМ краще використовувати інший підхід: перш за все треба зрозуміти, яку задачу розв'язує кожен з алгоритмів НАМ₁ і НАМ₂, потім по­слідовність цих задач об'єднати в спільну задачу і, наостанок, побу­дувати алгоритм для цієї загальної задачі.

В нашому прикладі алгоритм НАМ₁ замінює кожну букву Ь сло­вом аЬ, а потім алгоритм НАМ₂ видаляє букви Ь. Зрозуміло, що по­слідовне застосування спершу НАМ₁, а потім НАМ₂ замінює кожну букву Ь вхідного слова буквою а. Шукана композиція НАМ₁ і НАМ₂ має, наприклад, такий простий вигляд:

|ь ^ а .

Ми показали, що клас нормально обчислюваних функцій є до­сить широкий. Поняття нормально обчислюваної функції - одне з основних понять теорії алгоритмів. Його значення є таким. З одно­го боку, кожна стандартно задана нормально обчислювана функція є обчислювана за певною процедурою, яка відповідає інтуїтивному уявленню алгоритму, а з іншого - які б досі не будувалися класи то­чно визначених алгоритмів, завжди з'ясовувалося, що числові фун­кції, які обчислювалися за алгоритмами цих класів, були нормально обчислюваними. Тому загальноприйнятою є така наукова гіпотеза:

Теза Маркова-Черча. Будь-який алгоритм можна реалізува­ти з допомогою НАМ.

У формулювання цієї тези входить інтуїтивне поняття алгори­тму, тому його не можна ні довести, ні спростувати в загальномате- матичному значенні. Справидливість гіпотези підтверджується пра­ктикою: всі відомі алгоритми, які були придумані впродовж бага­тьох тисячоліть історії математики, можуть бути задані з допомо­гою НАМ. Проте, справедливою є наступна теорема, доведення якої читач може знайти в [?]:

7.9. теорема. Функція є обчислюваною за Тюрінґом тоді і тільки тоді, коли вона є частково рекурсивною тоді і тільки тоді, коли вона є нормально обчислюваною.

Вправи до лекції 7.

1. Побудувати НАМ, який обчислює числову функцію / : N0 — N0, /(п) = п той 2, якщо аргументи задані:

а) в унарній системі числення;

б) в двійковій системі числення;

в) в трійковій системі числення.

2. Побудувати НАМ, який обчислює числову функцію / : N0 — N0, аргументи якої задані в двійковій системі числення.

а) /(п) = 4ю • п;

б) /(п) = [п/2];

в) / (п) = [п/4].

3. Побудувати НАМ, який обчислює числову функцію / : N0 х N0 — N0, аргументи якої задані в унарній системі числення.

а) /(п, т) = п + т;

б) /(п, т) = тах{п, т};

в) /(п, т) = тіп{п, т};

4. Показати, що наступні частково визначені числові функції / : N0 — N0, аргументи яких задані в четвірковій системі числення, є нормально обчислювані:

а) / (п) = п + 1;

б) /(п)= п + 2;

в) /(п) = п — 2.

5. Показати, що наступний НАМ обчислює функцію / : N0 х^ — N0, /(п,т) = НСД(п, т), аргументи якої задані в унарній системі числення:

' |а — а| | * | — а* — *Ь < Ь — | .

а —> с

6. А = {0,1, 2, а}. З'ясувати чи є вхідне слово записом числа в трійковій системі числення. Відповідь: 1 - якщо є, 0 - в протилежно­му випадку.

7. А = {0,1, 2}. Вважаючи вхідне слово записом числа в трійковій системі числення, видалити з нього всі незначущі нулі.

8. А = {0,1}. Вважаючи непорожнє слово записом двійкового числа, визначити, чи є воно степенем двійки. Відповідь: слово 1, якщо є, або 0 в протилежному випадку.

9. А = {0,1}. Вважаючи непорожнє слово записом двійкового числа, перевести його в четвіркову систему числення. (Зауважен­ня: врахувати, що в двійковому числі може бути непарна кількість цифр.)

10. А = {|}. Перевести число з унарної системи числення в трій- кову. (Рекомендація: можна у циклі видаляти з унарного числа по палочці і кожен раз додавати 1 до трійкового числа, яке на початку покласти рівним 0.)

11. Для кожної пари НАМ побудувати їх композиції відносно ал­фавіту {0, 1}:

Р2 : {1 — 0

а) Рі : 01 10

' *0 — * *1 — 1*

* і—> —> *

б) Рз :

<

Р4 : {1 — 0

*0 — 1* *1 — 0*

* і—>

в) Рк :

7.12. Чи є НАМ зі схемою Р₃ композицією нормальних алгоритмів зі схемами Рі і Р₂ відносно алфавіту {0,1, 2}:

Рб : {01 —

Рі

01 10

^:

Р2 : {02 — 20

01 — 10 02 ^ 20

Лекція 8. Складність алгоритмів

В загальній теорії алгоритмів вивчається лише теоретична мо­жливість розв'язання задач. При розгляді конкретних задач не звер­тається увага на ресурси часу і пам'яті для відповідних алгоритмів- розв'язків. Але теоретична можливість розв'язання задачі не гаран­тує її практичної реалізації.

Введемо необхідні означення, відштовхуючись від машин Тюрін- га. Нехай машина Тюрінга обчислює словесну функцію / (х). Визна­чимо функцію іт (х), значення якої для слова х дорівнює кількості та­ктів машини Тюрінга Т, які виконуються при обчисленні /(х), якщо /(х) визначене. Якщо /(х) не визначене, то значення функції іт(х) теж вважається не визначеним. Функція іт(х) називається часовою складністю машини Тюрінга Т.

Активною зоною при роботі машини Тюрінга на слові х назива­ється називається множина всіх комірок стрічки, які містять непо­рожні букви, або відвідувались головкою машини Тюрінга в процесі обчислення. Визначимо функцію зт (х), значення якої дорівнює дов­жині активної зони при роботі машини Тюрінга Т на слові х, , якщо /(х) визначене. Якщо /(х) не визначене, то значення функції зт(х) теж вважається не визначеним. Функція зт (х) називається ємнісною складністю машини Тюрінга Т.

Введені функції іт (х) і зт(х) є словесними. Зручно ввести для розгляду функції натурального аргументу, поклавши:

іт(п) = тах{і_т(х)} і з_т(п) = тах{з_т(х)}.

|ж|=п |ж|=п

Ці функції теж називаються функціями часової і ємнісної складності (в найгіршому випадку) машини Тюрінга Т.

Рз :

Визначимо функції часової та ємнісної складності для алгори­тмів Маркова. Нехай алгоритм Маркова М обчислює словесну фун­кцію /(х). Визначимо функцію ім (х), значення якої для вхідного слова х дорівнює кількості підстановок, які виконується в процесі

обчислення вихідного слова / (х) з вхідного слова х, якщо алгоритм застосовний до вхідного слова х. Якщо ж алгоритм аналізуючи сло­во х ніколи не зупиниться, то значення функції ім (х) вважається не визначеним. Функція ім (х) називається часовою складністю алгори­тму Маркова М.

Визначимо функцію 8м (х), значення якої дорівнює максималь­ній з довжин слів, які виникають при обчисленні з вхідного слова х вихідного слова /(х), якщо /(х) визначене. Якщо /(х) не визначене, то значення функції 8м (х) теж вважається не визначеним. Функція 8м (х) називається ємнісною складністю алгоритму Маркова М.

Аналогічно як і для машини Тюрінґа, зручно ввести функції на­турального аргументу, поклавши:

ім(п) = тах{ім(х)} і 8м(п) = тах{8м(х)}.

|ж|=п |ж|=п

Ці функції теж називаються функціями часової і ємнісної складності (в найгіршому випадку) алгоритму Маркова М.

Гранична поведінка функцій іт і ім (відповідно 8т і 8м) при збільшенні розміру п задачі називається асимптотичною часовою (відповідно ємнісною) складністю. Для конкретних задач розгляда­ються як правило асимптотичні функції складності.

Нехай / і д - дві функції натурального аргументу. Кажуть, що /(п) = 0(д(п)) (читається: "еф від ен є о велике від же від ен"), якщо існує така константа с > 0, с Є Ж і таке число п₀ Є N0, що 0 < /(п) < сд(п) для всіх п > п₀. Запис /(п) = 0(д(п)) означає, що існують такі константи с₁, с₂ > 0, с₁, с₂ Є Ж і таке п₀ Є N0, що 0 < с₁ д(п) < /(п) < с₂д(п) для всіх п > п₀.

Кажуть, що машина Тюрінга (алгоритм Маркова) розв'язує за­дачу за поліноміальний час, якщо іт(п) = 0(р(п)) (ім(п) = 0(р(п))) для деякого многочлена р. В протилежному випадку кажуть, що ма­шина Тюрінга (алгоритм Маркова) розв'язує задачу за експоненці­альний час.

Часова складність алгоритму відображає потрібні для його ро­боти витрати часу. Аналогічно як для машини Тюрінґа і алгоритмів Маркова, для будь-яких алгоритмічних моделей часова складність визначається як функція, яка кожній послідовності вхідних даних довжини п ставить у відповідність максимальний (за всіма індиві­дуальними задачами довжиною п) час і(п), який витрачає алгоритм для розв'язання індивідуальних задач із цією довжиною. Про кон­кретну задачу кажуть, що вона розв'язується за поліноміальний час, якщо існує алгоритм (наприклад, машина Тюрінга чи алгоритм Мар­кова), який розв'язує цю задачу за поліноміальний час. Через Р по­значається клас всіх задач, які розв'язуються за поліноміальний час. В іншому випадку, кажуть, що задача розв'язується за експоненці­альний час. Задачу називають важкорозв'язною, якщо немає полі- номіального алгоритму для її розв'язання.

Вважається, що поліноміальні алгоритми відповідають швидким, ефективним на практиці алгоритмам, а поліноміально розв'язні за­дачі відповідають легким задачам, які можуть бути розв'язаними за прийнятний час на входах довжини, що має практичний інтерес. Часто поліноміальний алгоритм справді задовольняє всі практичні потреби. В гіршому ж випадку його можна вважати швидким лише асимптотично, а на відносно невеликих входах алгоритм може пра­цювати довго. Слід підкреслити, що клас поліноміально розв'язних задач не залежить від того, яка саме з багатьох можливих формаліза- цій алгоритму вибрана. Цей факт можна строго довести як теорему для будь-яких означень алгоритму.

Слід зазначити, що є експоненціальні алгоритми, які добре заре­комендували себе на практиці. Річ у тім, що часову складність озна­чено як міру поведінки алгоритму в найгіршому випадку. Насправді може виявитись, що для розв'язання більшості конкретних задач по­трібно значно менше часу, і це дійсно так для деяких добре відомих алгоритмів. Наприклад, симплекс-метод для розв'язування задач лі­нійного програмування має експоненціальну часову складність, але дуже добре працює на практиці.

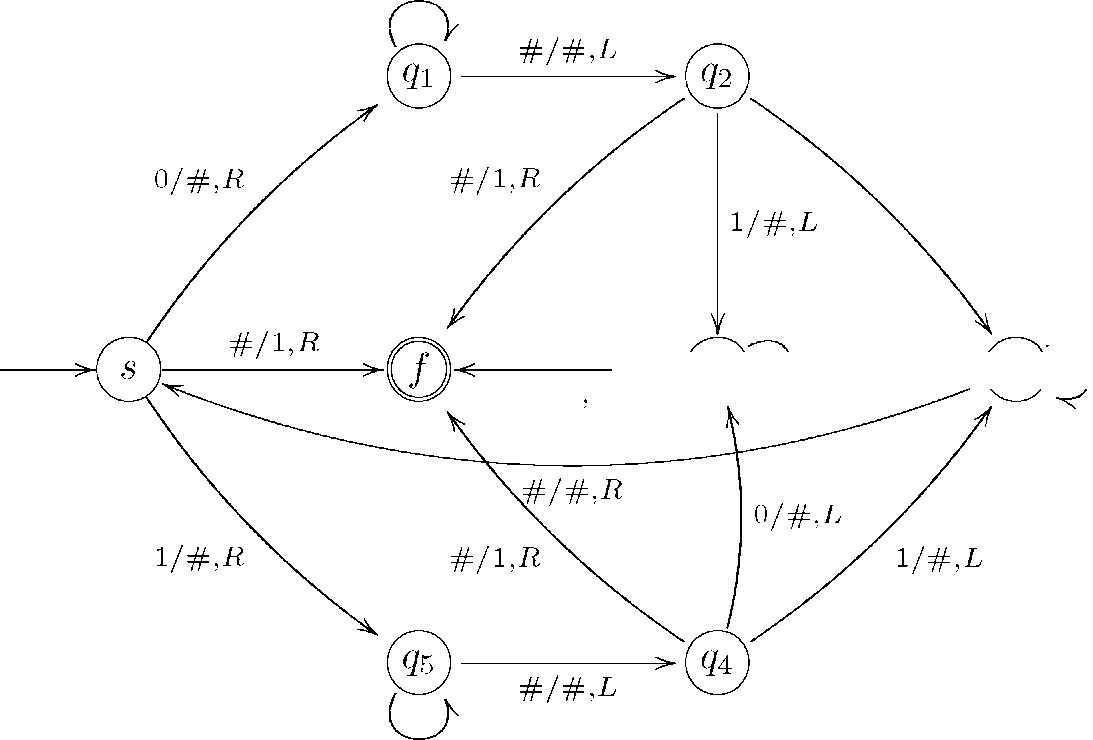
8.1. Приклад. Побудувати машину Тюрінга, яка в алфавіті А = {0,1} для будь-якого слова Р = р₁ р₂ .. .р_п визначає чи є воно симе­тричним, тобто Р = р₁ р₂ . . .р_п = РпРп_-1 . . .р₁ = Р'. Відповідь: слово 1, якщо слово Р симетричне, 0 - в протилежному випадку. Оцінити часову та ємнісну складність побудованої машини Тюрінга.

Граф шуканої машини Тюрінґа має вигляд:

Робота машини Тюрінга здійснюється циклами. Впродовж пер­шого циклу машина перевіряє, чи виконуться рівність р₁ = р_п. Для цього в стані 5 запам'ятовується буква р₁ і головка машини Тюрінга в станах д₁ або зміщується вправо доти, доки не знаходить букву р_п і порівнює її з р₁ в станах д₂ або . Якщо ці букви різні, то машина переходить в стан , стирає слово на стрічці і друкує букву 0, в про­тилежному випадку машина здійснює другий цикл, впродовж якого порівнює букви р₂ та р_п-1 і т. д. Зрозуміло, що найбільшу кількість тактів машина Тюрінґа виконує на симетричних словах довжини п. Якщо симетричне слово Р має парну довжину, то буде проведено п/2 повних циклів порівнянь букв, впродовж яких буде здійснено число тактів, яке дорівнює

(2п + 1) + (2(п - 2) + 1) + ... + 5 =

(2п + 1) + 5 п _ (п + 3)п 2 = '

2 2 2 Після цього машина здійснює ще один такт і зупиняє роботу.

0/0,1/1,Д

0/#,Ь

0/0,1/1,Д

#_/0д ^^ 0/#,1/#,ь_{дз) )0/0,1/1,ь

Якщо ж симетричне слово Р має непарну довжину, то буде про­ведено (п — 1)/2 повних циклів порівнянь букв, впродовж яких буде здійснено число тактів, яке дорівнює

(2п + 1) + (2(п — 2) + 1) +'.' + 7 =

2

(2п + 1) + 7 п — 1 (п + 4)(п — 1)

Далі, МТ здійснює ще три такти і переходить в кінцевий стан.

З проведених вище міркувань і аналізу графа машини Тюрінга випливає, що зт (п) = п + 1 < 2п, зт (п) = О(п), а функція часової складності має вигляд

(п+3)і

п + 3п + 2 2

2

+ 1,п = 2к,к є N

^іт^(п) = < (п+4)(п-1)

+ 3, п = 2к - 1, к є N

Оскільки ^п2+І^п+2 < ^п2+3п²+^2п = 3п², то і_т(п) = О(п²) і задача розв'язується за поліноміальний час, тобто належить класу Р.

8.2. Приклад. Проаналізувати роботу алгоритму Маркова, заданого над алфавітом А = {а₁, а₂,..., а_т}, та оцінити його складність:

** — #

#а — а#, де а є А #* — #

# —

*аЬ — Ь * а, де а,Ь є А

Якщо Р = ^Ь₂ .. .Ь_п, то оберненням слова Р називається слово Р' = Ь_пЬ_п-1 .. . Покажемо, що алгоритм здійснює обернення слів в алфавіті А. Дійсно, нехай маємо деяке слово Р в алфавіті А. Тоді: Р — *Р — Ь2 * Ьі .. .Ьп — Ь2 Ьз * Ьі Ь4 . . .Ьп — ... — Ь2 Ьз .. .Ьп * Ьі —

*Ь2Ьз... Ьп*Ьі

Ьз Ьа ... Ьп * Ь2 * Ьі

*Ьп * Ьп-1 . . .*Ь2 *Ьі

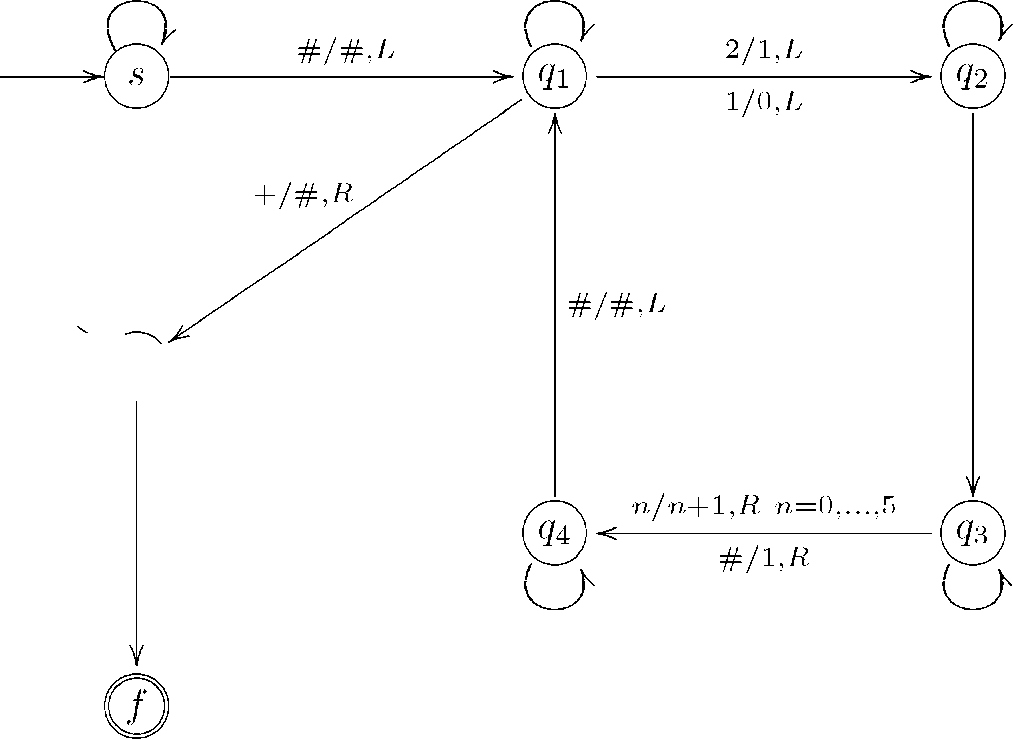
Очевидно, що алфавіт А = {0,1, 2,3, 4, 5, 6, +}. Множина станів складається з семи елементів: ^ = {з,д₁ ,д₂,д₃,д₄,д₅, /}. Нехай до­данки відокремлюються знаком +, порожні секції, як і раніше, по­значатимемо і нехай на стрічці ліворуч від знака + розміщено доданок у сімковій системі числення, а праворуч - доданок у трійко- вій системі числення. Ідея розв'язання задачі така: спочатку в стані 5 переміщуємося до останнього символу, потім від числа, розміще­ного праворуч, в стані д₁ віднімаємо одиницю, діючи за правилами трійкової арифметики, після чого в стані д₂ просуваємося ліворуч та до сімкового числа додаємо одиницю в стані д₃, діючи за правилами сімкової арифметики. Далі, повертаємося до правого числа з допо­могою стану д₄ і переходимо в стан д₁. Повторюємо всі операції доти, доки доданок, розміщений праворуч від знака +, не буде вичерпано.

Оцінимо складність даного алгоритму. Очевидно, що функція іт(х) буде приймати максимальне значення на словах х довжини п виду: а+Ь₁Ь₂ ... Ь_п-2. Оцінимо на стільки може збільшитися довжина слова в процесі додавання. Оскільки

Ьі Ь2 ...Ьп-2 = Ьі 3^п-3 + Ь2 3^п-4 + ... + Ьп-3 3 + Ьп-2 < 3^п-2,

+ /+,п/п,Д п=0,...,б

0/2 ,Ь

#/#,Ь

+/+,Ь

+ /+,п/п,Д п=0,...,б

0/0,1/1,2/2 ,Ь

2/#,к( (Об)

то при додаванні цього числа в ліву частину загальна довжина слова збільшиться не більше ніж на 1од₇ 3^п-2 = (п — 2) 1од₇ 3. Враховуючи

крайні порожні клітинки і той факт, що кількість циклів, які здій­снить машина Тюрінга при додаванні, не перевищує 3^П-2 маємо, що ємнісна складність

8_Т(п) < п 1од₇ 3 — 1од₇ 9 + п + 2 = О(п),

а часова складність

іт(п) < 2(п 1од₇ 3 — 1од₇ 9 + п + 2)3^п-2 = О(п3^п).

Отже, дана машина Тюрінга розв'язує задачу за експоненціаль­ний час.

Вправи до лекції 8.

1. Чи можна стверджувати, що а) 2^П+1 = О(2^п); б) 2^2п = О(2^п)?

2. Довести, що для полінома /(п) = а_тп^т + ... + а₁ п + а₀, де а_т > 0, аі Є Ж, і = 1,т, має місце рівність /(п) = 0(п^т).

3. Доведіть, що /(п) = п⁰⁽¹⁾ тоді і тільки тоді, коли існує таке додатнє т, для якого /(п) = О(п^т) (вважаємо, що /(п) > 1).

4. Побудувати поліноміальний нормальний алгоритм Маркова в алфавіті {а, Ь} з часовою складністю О(1), який витирає у вхідному слові, яке містить не менше ніж три букви, третю букву?

5. Побудувати ефективні нормальний алгоритм Маркова та ма­шину Тюрінґа, які обчислюють функцію / (п) = п — 3 натуральних четвіркових аргументів. Оцінити їх часову та ємнісну складність.

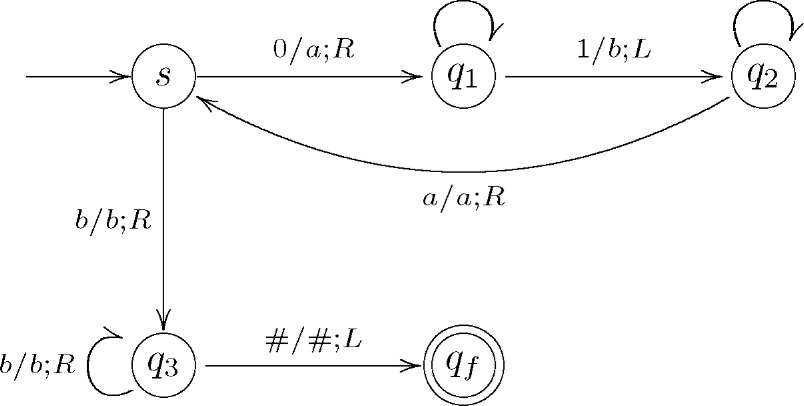
6. Нормальний алгоритм Маркова (А,Р) задається схемою

* і—> —> *

V

Оцінити його часову та ємнісну складність.

Ьа# ^ а#Ь, де а,Ь Є А ^ а#ал, де а Є А

0/0,Ь/Ь;П 0/0,Ь/Ь;Ь

8.8. Показати, що наступний НАМ обчислює функцію / : N0 х^ — N0, /(п, т) = пт, аргументи якої задані в унарній системі числення:

'Ь| — ІЬ о\ — |Ьа а —

< |* — *а . *| — *

* —