
- •1. Цель работы:
- •2. Основные теоретические сведения.
- •3.1 Анализ чувствительности оптимального решения злп к
- •3.2. Анализ чувствительности оптимального решения
- •3.3. Анализ чувствительности оптимального решения
- •Новое оптимальное решение
- •Анализ чувствительности оптимального решения злп к вариациям коэффициентов целевой функции
- •Анализ чувствительности оптимального решения злп к введению нового ограничения
3.3. Анализ чувствительности оптимального решения
ЗЛП к введению нового ограничения.
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно менее жесткие ограничения исходной задачи отброшены. Тогда, получив решение, необходимо убедиться в том, что отброшенные ограничения являются действительно несущественными. И, если это не так, то необходимо найти новое решение с учетом невыполняющихся ограничений.
Введение нового ограничения в ЗЛП в общем случае может привести к деформации (уменьшению) области ее допустимых решений. Эта деформация будет существенной лишь тогда, когда она приводит к отсечению оптимального решения. Например, так как показано на рио.3.6.
О
Новое ограничение
X[2]
Grad Z
Старое оптимальное
решение









 пределение
нового оптимального решения, если новое
ограничение не приводит к пустоте
допустимого множества, находится
графическим способом, как и первоначальное.
пределение
нового оптимального решения, если новое
ограничение не приводит к пустоте
допустимого множества, находится
графическим способом, как и первоначальное.
Рис.
3.6 Геометрическая интерпретация введения
нового ограничения
X[1]



Новое оптимальное решение

 ормальный
анализ чувствительности оптимального
решения к введению нового ограничения
может быть проведен следующим образом.
Проверка того, отсекает или нет новое
ограничение найденное оптимальное
решение от допустимой области,
делается подстановкой оптимального
базисного решения в новое ограничение.
Будем предполагать, что вводится новое
ограничение
ормальный
анализ чувствительности оптимального
решения к введению нового ограничения
может быть проведен следующим образом.
Проверка того, отсекает или нет новое
ограничение найденное оптимальное
решение от допустимой области,
делается подстановкой оптимального
базисного решения в новое ограничение.
Будем предполагать, что вводится новое
ограничение
![]() в виде неравенства вида:
в виде неравенства вида:
![]() (3.14)
(3.14)
где
![]() - число переменных исходной ЗЛП.
- число переменных исходной ЗЛП.
Тогда проверка заключается в проверке истинности неравенства
![]() (3.15)
(3.15)
Если
неравенство 3.15 не выполняется, то
необходимо осуществить поиск нового
оптимального решения или убедиться в
пустоте допустимого множества задачи
с учетом вновь введенного ограничения.
Это может быть сделано путем введения
нового ограничения в заключительную
симплекс-таблицу и осуществления поиска
нового решения задачи, начиная с этой
скорректированной симплекс-таблицы.
Обоснование такой возможности состоит
в том, что коэффициенты действительной
части симплекс-таблиц
![]() и
и
![]() представляют собой многократно
преобразованные по Гауссу-Жордану
коэффициенты исходных ограничений. Для
симплекс-таблицы
,
в этом просто убедиться на основе анализа
следующих соотношений:
представляют собой многократно
преобразованные по Гауссу-Жордану
коэффициенты исходных ограничений. Для
симплекс-таблицы
,
в этом просто убедиться на основе анализа
следующих соотношений:
![]() (3.16)
(3.16)
![]() ,
(3.17)
,
(3.17)
где
![]()
Для введения нового ограничения в симплекс-таблицу с новым ограничением нужно сделать такие же преобразования, какие были бы осуществлены с ним в процессе поиска прежнего решения. Вид этих преобразований можно установить из анализа структуры любой i-й строки симплекс-таблицы, определяющей эквивалентно преобразованное i-е ограничение исходной задачи:

![]() (3.18)
(3.18)![]()
Рис.
3.7 Соответствие с-т
![]() и преобразованных ограничений
и преобразованных ограничений
Из 3.18 видно, что в левой части преобразованного ограничения при базисной переменной, соответствующей данной строке, коэффициент равен единице, при остальных же базисных переменных коэффициенты равны нулю, т.е. все базисные переменные из нового ограничения должны быть выведены. К такому же виду должно быть преобразовано и новое ограничение. Алгоритм преобразования будет следующим:
I. Привести ограничение 3.14 к каноническому виду:
![]() (3.19)
(3.19)
где
![]() - количество переменных в канонической
форме исходной ЗЛП;
- количество переменных в канонической
форме исходной ЗЛП;
![]() -
новая базисная переменная.
-
новая базисная переменная.
2.
Исключить из ограничения (3.19) все
переменные, являющиеся базисными в
оптимальном решении ЗЛП, полученном
без ограничения (3.14). Выполнение 2-го
пункта алгоритма может быть очень просто
осуществлено с помощью той же заключительной
симплекс-таблицы. Чтобы, например,
исключить переменную
![]() из ограничения 3.19 нужно вычесть из него
ограничение 3.18, умноженное на
из ограничения 3.19 нужно вычесть из него
ограничение 3.18, умноженное на
![]() .
Рабочий алгоритм расширения
заключительной симплекс-таблицы
будет следующим:
.
Рабочий алгоритм расширения
заключительной симплекс-таблицы
будет следующим:
1. Расширить базисное множество, поставив на последнее место номер (n+1).
2. Сдвинуть на одну строку вниз последнюю строку симплекс-
таблицы .
На место сдвинутой строки записать в соответствующем порядке коэффициенты нового ограничения.
Добавить к симплекс-таблице новый столбец, соответствующий n+1 -ой базисной переменной,
Из вновь образованной в п.З строки вычитать поочередно каждую i-ую строку (i=1,m) заключительной симплекс таблицы, умноженную соответственно на .
Рис.
3.8 Расширенная с-т
![]()
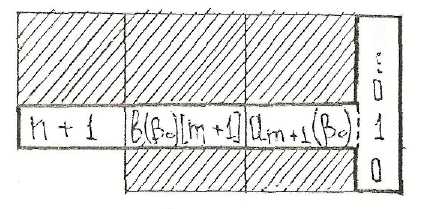 имплекс-таблицу
имплекс-таблицу
![]() ,
изображенную на рис. 3,8. В ней выделена
та ее часть, которая добавляется вновь,
а заштрихованная часть соответствует
прежней симплекс-таблице
,
изображенную на рис. 3,8. В ней выделена
та ее часть, которая добавляется вновь,
а заштрихованная часть соответствует
прежней симплекс-таблице
![]() .
.
Расширение
симплекс-таблицы
![]() может быть осуществлено аналогичным
образом, если учесть, что обратная
матрица получается в результате
эквивалентных преобразований
Гаусса-Жордана столбцов матрицы условий
вспомогательной задачи при фиктивных
переменных. В соответствии с этим
представлением в п.3 предыдущего алгоритма
во вновь образуемую m+1-ую
строку расширенной обратной матрицы
первоначально должны быть записаны
нули. Добавление же нового столбца
осуществляется вставкой его на
предпоследнее место с предварительным
сдвигом последнего с
может быть осуществлено аналогичным
образом, если учесть, что обратная
матрица получается в результате
эквивалентных преобразований
Гаусса-Жордана столбцов матрицы условий
вспомогательной задачи при фиктивных
переменных. В соответствии с этим
представлением в п.3 предыдущего алгоритма
во вновь образуемую m+1-ую
строку расширенной обратной матрицы
первоначально должны быть записаны
нули. Добавление же нового столбца
осуществляется вставкой его на
предпоследнее место с предварительным
сдвигом последнего с толбца
заключительной с-т
на один вправо.
толбца
заключительной с-т
на один вправо.
В
результате получим расширенную
симплекс-таблицу
![]() изображенную на рис. 3.9
изображенную на рис. 3.9
Рис. 3.9 Расширенная симплекс-таблица .
Если
найденное оптимальное решение не
удовлетворяет новому ограничению, то
при расширении симплекс-таблицы величина
![]() окажется отрицательной. Прежний базис
останется сопряженным (как и при
варьировании правой части ограничения
больше предельной величины). Для
нахождения нового решения необходимо
применять алгоритм двойственного
симплекс-метода. В результате его работы
либо будет найдено новое оптимальное
решении, либо будет установлено, что
новое ограничение превращает
допустимую область ЗЛП в пустое множество.
окажется отрицательной. Прежний базис
останется сопряженным (как и при
варьировании правой части ограничения
больше предельной величины). Для
нахождения нового решения необходимо
применять алгоритм двойственного
симплекс-метода. В результате его работы
либо будет найдено новое оптимальное
решении, либо будет установлено, что
новое ограничение превращает
допустимую область ЗЛП в пустое множество.
3. СОДЕРЖАНИЕ РГР ПО КУРСУ ТОПУ
«Анализ чувствительности оптимального решения ЗЛП к вариациям ее параметров»
