МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(государственный технический университет)

Хахулин Г.Ф.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для выполнения расчетно-графической работы

"Исследование чувствительности оптимального решения задачи линейного программирования к вариациям ее параметров и введению нового ограничения"

по дисциплине "Теория оптимального планирования и управления"

Москва 2010

Содержание

1. Цель работы

2. Основные теоретические сведения

2.1 Анализ чувствительности оптимального решения ЗЛП к вариациям коэффициентов целевой функции

2.2 Анализ чувствительности оптимального решения к вариациям правых частей ограничений

2.3 Анализ чувствительности оптимального решения ЗЛП к введению нового ограничения

3.Содержание отчета

1. Цель работы:

Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и вве­дению нового ограничения. Получение навыков практического решения такого рода задач.

2. Основные теоретические сведения.

Необходимость анализа чувствительности задачи математического программирования к вариациям ее параметров может возникнуть в следую­щих случаях:

• при анализе влияния на результат оптимизации ошибок в исходных данных, на основе которых формируются параметры ЗЛП;

• при определения наилучшей вариации параметров, когда их выбор находится в руках лица, принимающего на основе результатов оптимизации решение по реализации оптимальных значений переменных;

• при внесении в задачу после получения ее решения изменений, связанных с дополнительной информацией.

При проведении такого анализа может возникнуть потребность в ответе на следующие вопросы:

• в каких пределах можно варьировать параметры задачи, чтобы прежнее оптимальное решение оставалось неизменным;

• остается ли прежнее решение допустимым, оптимальным при осуществлении определенных изменений параметров исходной задачи;

• если прежнее решение задачи стало недопустимым или неоптимальным, то каково будет новое решение задачи.

Анализ такого рода будет эффективным, если он не требует многократного повторного решения исходной задачи при различных значениях ее параметров. Широкие возможности в проведении исследования чувст­вительности имеются для задач линейного программирования при примене­нии к их решению методов симплекс-таблиц.

3.1 Анализ чувствительности оптимального решения злп к

вариациям коэффициентов целевой функции.

X[2]

Градиент

огр-я 2

В

1

0

5

X[1]

2

2

3

4

Градиент

огр-я 3

ариации коэффициентов целевой функции ЗЛП приводят к измене­нию направления вектора градиента. Так как при этом не затрагивается допустимое множество, то прежнее решение остается допустимым базис­ным, а оптимальное решение может измениться.

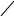
3.1 Графический способ анализа чувствительнос­ти оптимального решения к вариациям C[j].

Н

3

а рис. 3.1 приведены результаты графического анализа чувствительности оптимального решения ЗЛП к вариациям коэффициентов целевой функции. Оптимальное решение достигается в крайней точке под номером 4. Определены предельные положительные и отрицательные вариации коэффициентов целевой функции , которые находятся из условия возможности изменения направления Z внутри конуса, определяемого векторами-градиентами активных ограничений 2 и 3.

П ри положительной вариации больше предельной оптимальное решение переместится в крайнюю точку(КТ) 3, а при отрицательной - в КТ 5. О трицательная вариация больше предельной ( ) приведет к перемещению оптимального решения либо в КТ 3, либо в КТ 2.

Формальный анализ чувствительности оптимального решения к вариа­циям коэффициентов целевой функции может быть произведен с использова­нием заключительной симплекс-таблицы . Структура симплекс-таблицы для ручного счета имеет следующий вид:

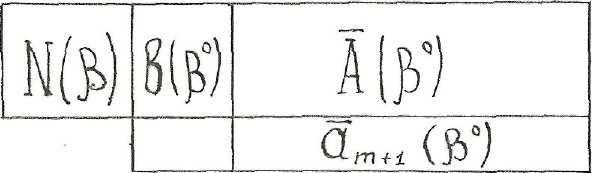
Рис. 3.2 Структура симплекс-таблицы

Вариации коэффициентов целевой функции приводят к изменению симплекс-разностей . В заключительной симплекс-таблице все симплекс-разности неположительны. Предельная величина вариации коэффици­ента целевой функции определяется из условия такого изменения симплекс-разностей, при котором одна из них, увеличиваясь, раньше всех станет равной нулю. Тогда дальнейшее изменение указанного коэффициента в том же направлении приведет к тому, что эта симплекс-разность станет положительной и, следовательно, прежнее значение перестанет быть оптимальным.

Ф ормула расчета симплекс-разности для каждого j-го столбца симплекс-таблицы имеет следующий вид:

(3.1)

где -коэффициенты целевой функции при базисных переменных;

-коэффициенты матрицы , являющейся составной частью симплекс-таблицы .

Анализ этой формулы позволяет выделить два случая:

• варьируется ;

- варьируется ,

где - базисное множество, соответствующее оптималь­ному решению

В первом случае будет меняться лишь симплекс-разность k-о столбца

(3.2)

К изменению оптимального решения при этом может привести лишь положительная вариация , которую можно определить, приравняв соотношение (3.2) к нулю:

(3.3)

Предельные отрицательные вариации по коэффициентам целевой функции небазисных переменных равны:

(3.4)

Рассмотрим второй случай

Пусть . Тогда:

(3.5)

Очевидно, что при вариациях такого будет изменяться не одна симплекс-разность, а все те из них, которым в l-ой строке матрицы соответствуют ненулевые коэффициенты.

(3.6)

При этом увеличиваться симплекс-разности будут в следующих случаях:

• при положительных вариациях 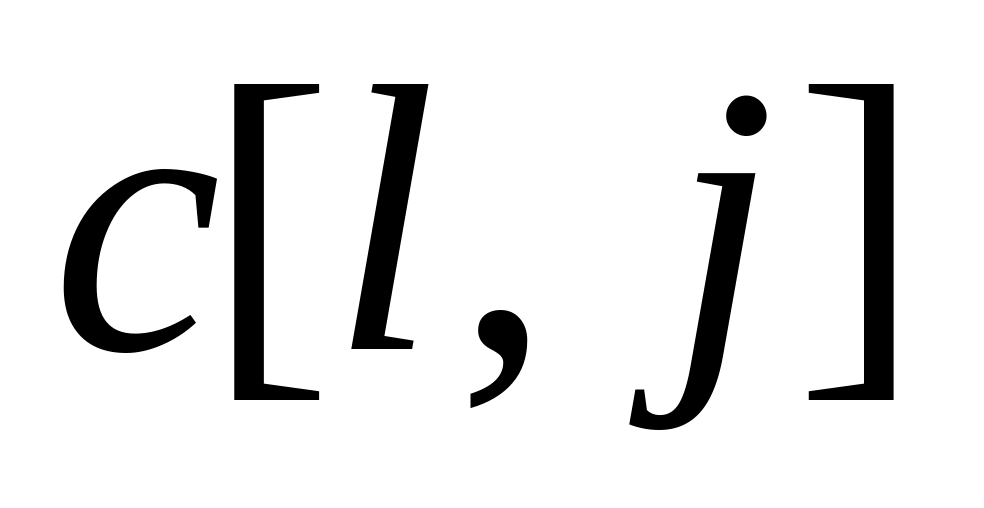, если ;

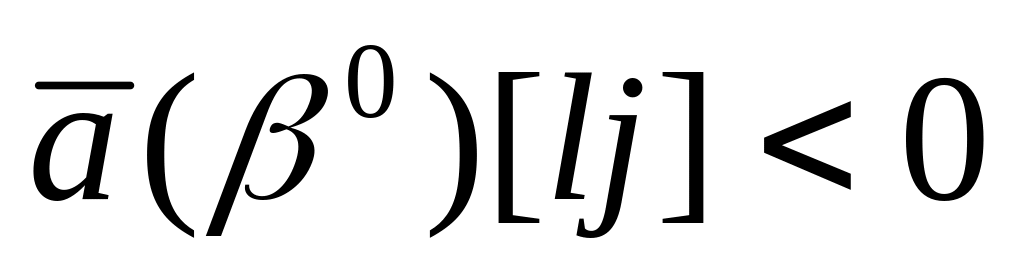• при отрицательных вариациях , наоборот, если

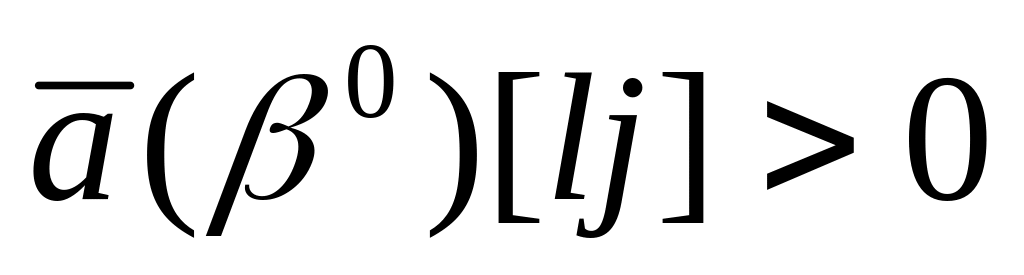
В соответствий с этими рассуждениями формулы для определения предельных вариаций коэффициентов целевой функции для случая имеют вид:

(3.7)

(3.8)

где (3.9)

Если произведена вариация больше предельной, то, чтобы найти новое решение ЗЛП, необходимо:

- скорректировать строку симплекс-разностей (для базиса ), ставшего теперь уже неоптимальным , а в случае и величину определяющую значение целевой функции:

где рассчитываются с учетом проведенной вариации;

- применить к скорректированной симплекс-таблице алгоритм поиска оптимального решения,

В результате его работы либо будет найдено новое оптимальное решение, либо установлено, что целевая функция при данной вариации неограничена на допустимом множестве. Последнее реализуется в том случае, если допустимое множество имеет образующие, и градиент целевой функции изменял свое направление таким образом, что стал образо­вывать острый угол с направляющим векторов хотя бы одной из них.