УДК 510.647

Э.В. Недоступов, д.A.. Саранча, Чигерев е.H., ю.C.Юрезанская о некоторых свойствах одномерных унимодальных отображений

Введение

Одномерное унимодальное отображение (ОУО) является одним из популярных объектов, иллюстрирующих богатство динамических режимов в простых разностных уравнениях. Получены такие результаты как «порядок Шарковского», каскады удвоений [1, 2]. В данном сообщении проведено исследование ОУО, полученных при описании динамики численностей животных. Для ОУО такого типа существует сценарий изменения выделенного параметра, при котором последовательно возникают зоны стабильности с устойчивыми циклами. Внутри зоны стабильности период циклов постоянный, при переходе от одной зоны к другой период изменяется в последовательности натурального ряда 1, 2, 3, 4…. Зоны стабильности отделены друг от друга переходными зонами с более сложными режимами. Предложены оригинальные способы нахождения периодических траекторий ОУО.

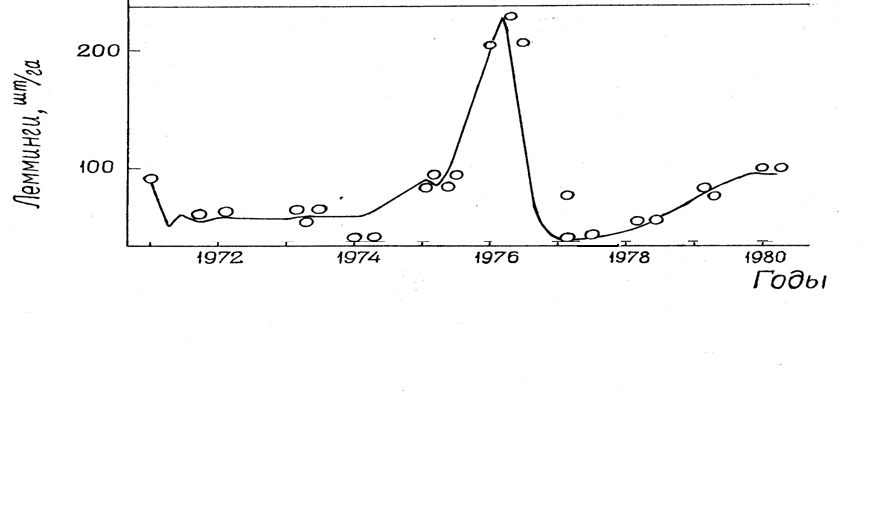
Рис.1. Результаты одного из имитационных экспериментов с моделью растительность – лемминги – песцы (сплошная кривая) и зарегистрированная на острове Врангеля динамика изменения численности копытного лемминга (круги).

Происхождение задачи

Задача об изучении свойств дискретных отображений (функций последования) возникла при описании динамики численности тундровых животных в рамках математических моделей тундровых популяций и сообществ [3-5]. Особую остроту исследований придал тот факт, что для популяции леммингов Западного Таймыра типичными являются чередование максимумов численности через три года. В то же время цикл периода три в порядке Шарковского, число три имеет некий мистический налет: если «появляется тройка» (цикл с периодом три), то в системе может реализоваться «все, что угодно», точнее циклы любой длины.

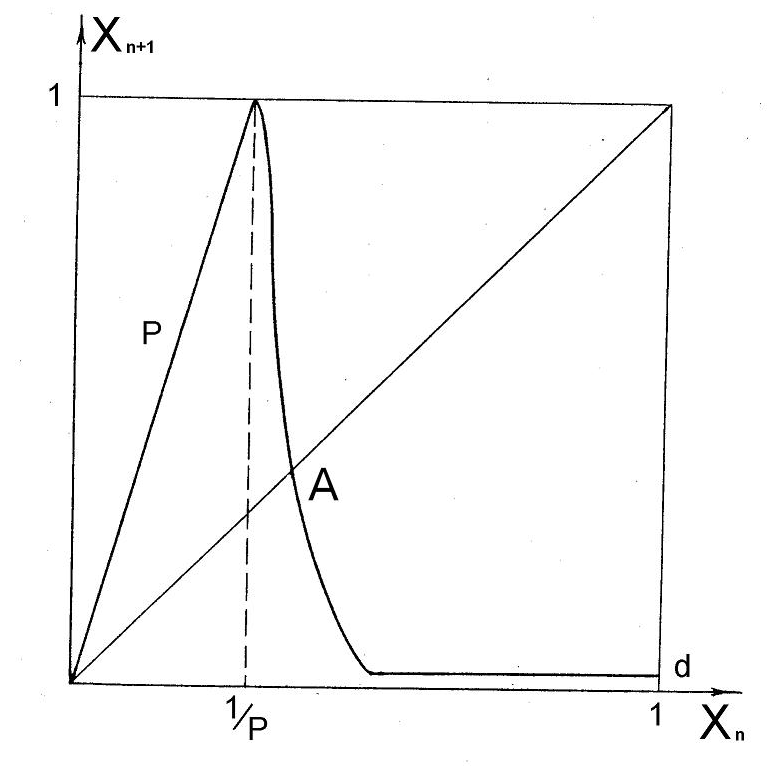
Рис.2. Вид базовых дискретных уравнений Xt+1=F(Xt), связывающих численности леммингов Xt в двух соседних годах, полученных в результате анализа моделей тундровых популяций и сообществ. Где P - скорость прироста биомассы леммингов в благоприятный год, A – равновесная численность, d – численность леммингов в оптимальном биотопе.

В результате проведенных исследований удалось построить набор взаимосвязанных моделей. Основа набора - подробные имитационные модели, построенные во взаимодействии с биологами. Анализ результатов вычислительных экспериментов с взаимодополняющими моделями сообщества «растительность-лемминги-песцы» (РЛП) и популяции леммингов (рис.1), привел к обоснованию упрощенных моделей в виде дискретных уравнений. C помощью дискретных уравнений X^t+1=F(X^t), связывающих численности леммингов X^t в двух соседних годах, удается воспроизвести временную динамику, качественно близкую к динамике численностей реальных популяций леммингов [3-5]. На рис.2 представлен вид дискретных уравнений, связывающих численности леммингов в двух соседних годах, полученных в результате анализа моделей тундровых популяций и сообществ. Эти уравнения легли в основу построения функций дискретных отображений только в целях изучения свойств дискретных отображений.

В уравнении, представленном в графическом виде на рис. 2, два ведущих показателя P – скорость прироста биомассы в благоприятный год и d – численность леммингов в оптимальном биотопе. Первый показатель оценивается сравнительно надежно, а второй – только по косвенным данным, фактически в результате подбора такого его значения, которое обеспечивает зарегистрированную динамику чередования максимумов численности леммингов. В связи с этим необходимо было проанализировать влияние этого параметра на динамику численности.

Как показали проведенные исследования (см. ниже) в подавляющем диапазоне изменения параметра d модель является грубой – при малом его изменении периодичность колебаний не изменяется. В то же время в определенном диапазоне появляется негрубость, когда малые изменения параметра d приводят к существенному изменению периодичности. Это происходит в окрестности положения равновесия A, и его прообразов F^-n(A) (см. ниже). Отметим, что «ширина» этой окрестности может быть сделана как угодно малой при «увеличении крутизны» кривой в переходной области от максимального значения до «ступеньки». В связи со сказанным выше, сценарий изменения параметра d адекватен рассматриваемой задаче.

Распространение данного сценария на другие функции происходил следующим образом. При выбранном значения d рассматриваемая функция оставалась неизменной до максимального значения, и на стадии спада до ее пересечения со ступенькой (при x<F^-1(d)), далее ее значение приравнивалось d. В этом случае рассматривается как бы ситуация старта траектории с разных начальных значений. Отметим, что при этом траектории могут достаточно долго «блуждать» до возвращения на ступеньку, с последующим повторением траектории.