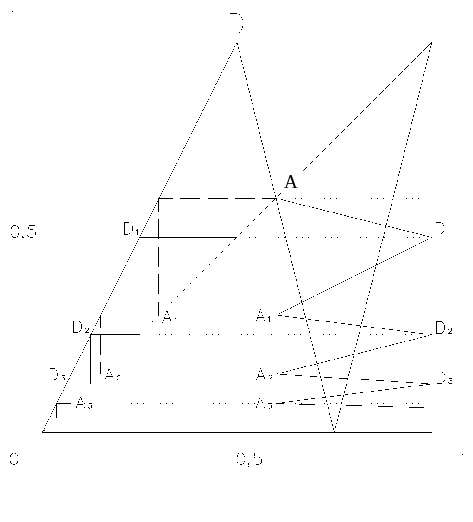Исследование треугольного, двухзонного и логистического дискретных отображений

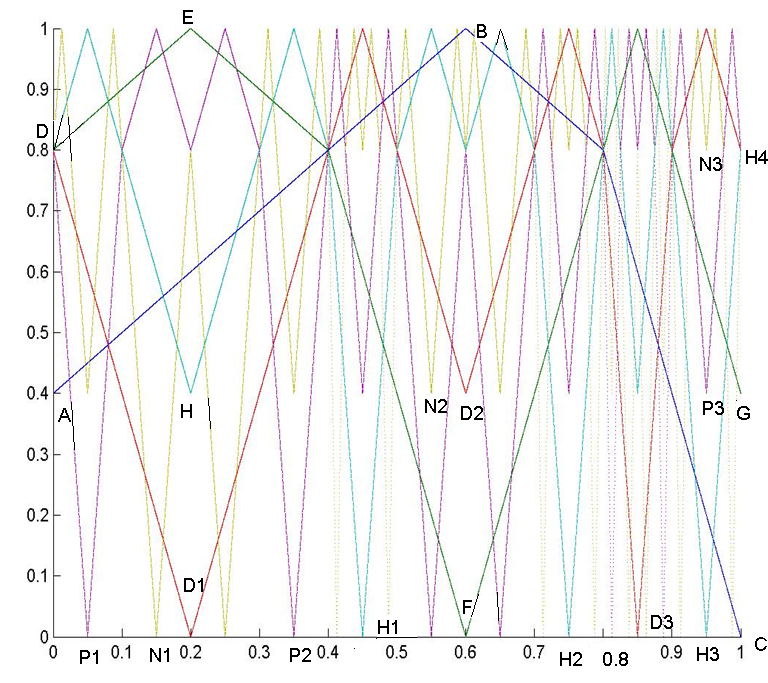
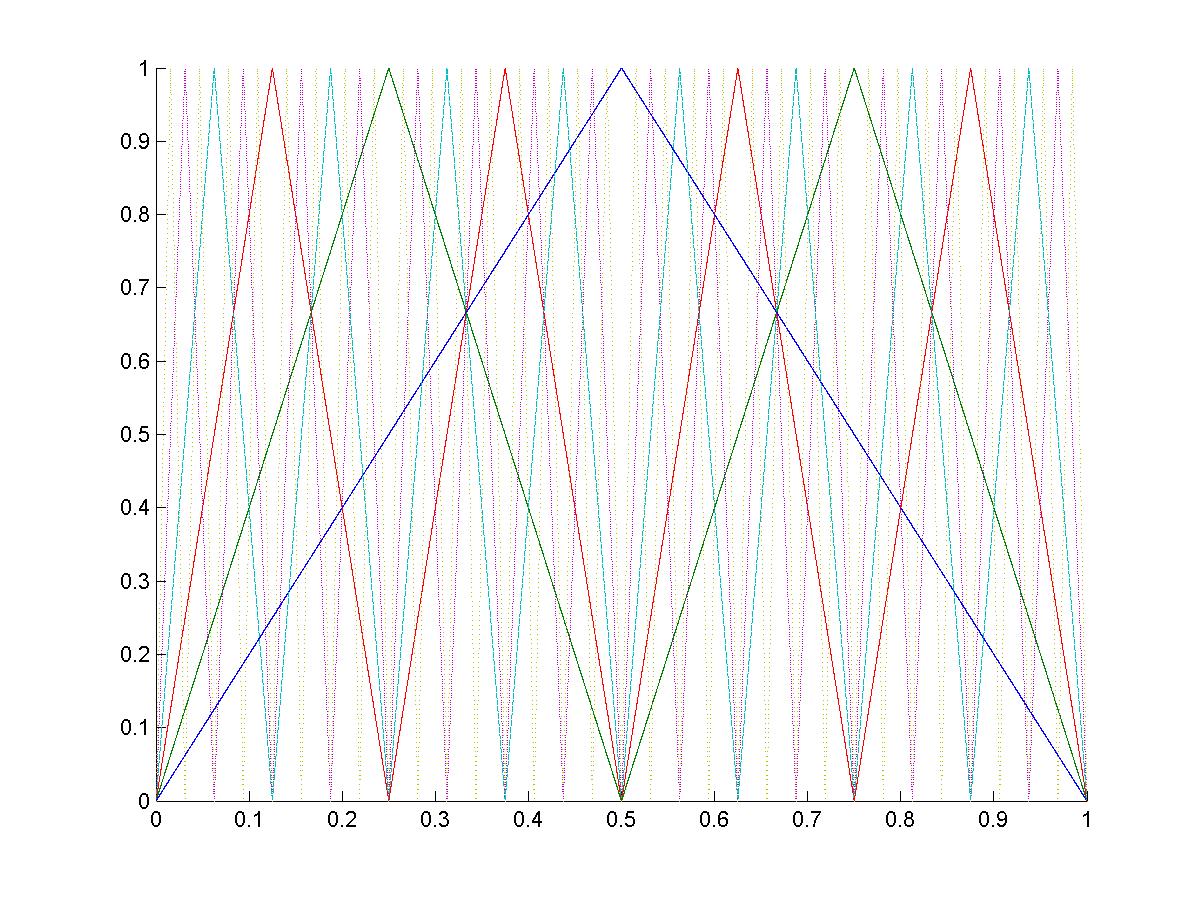
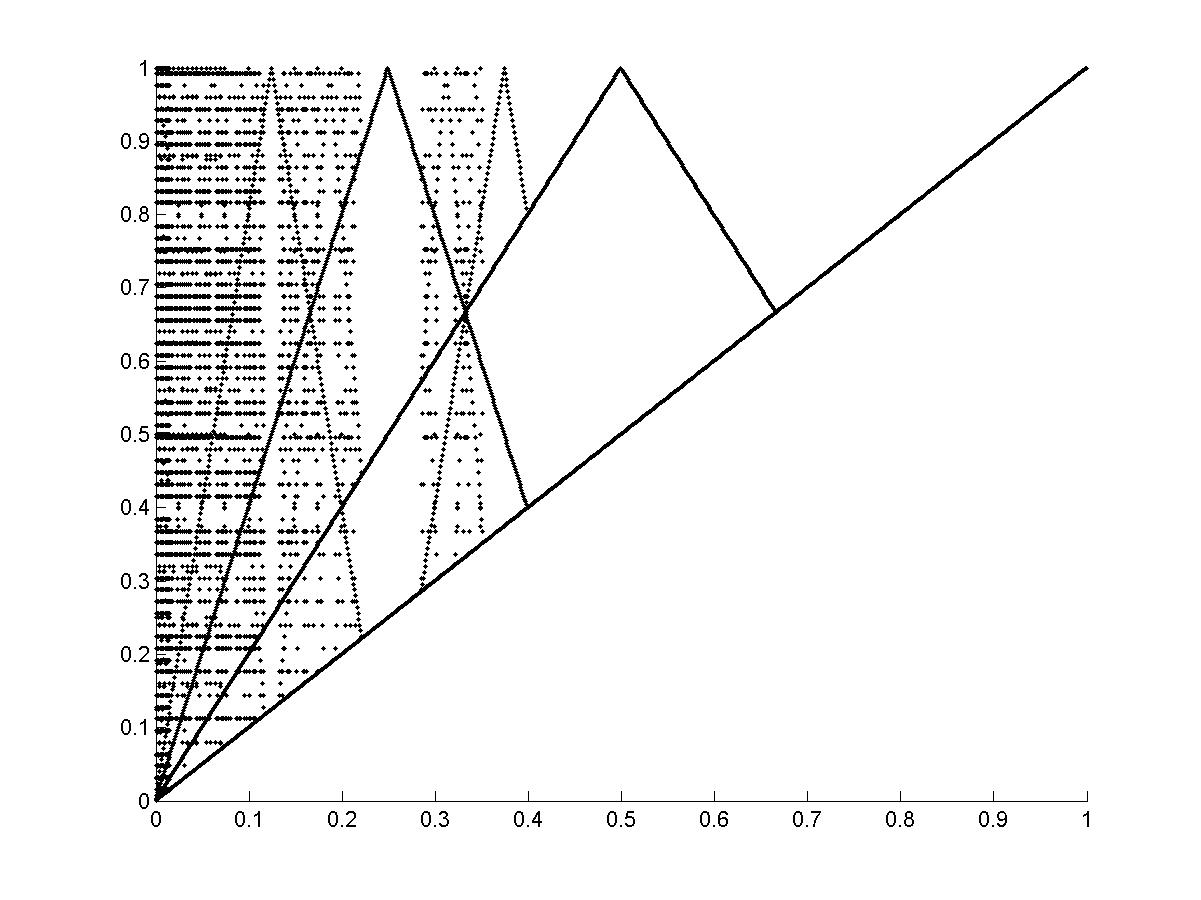
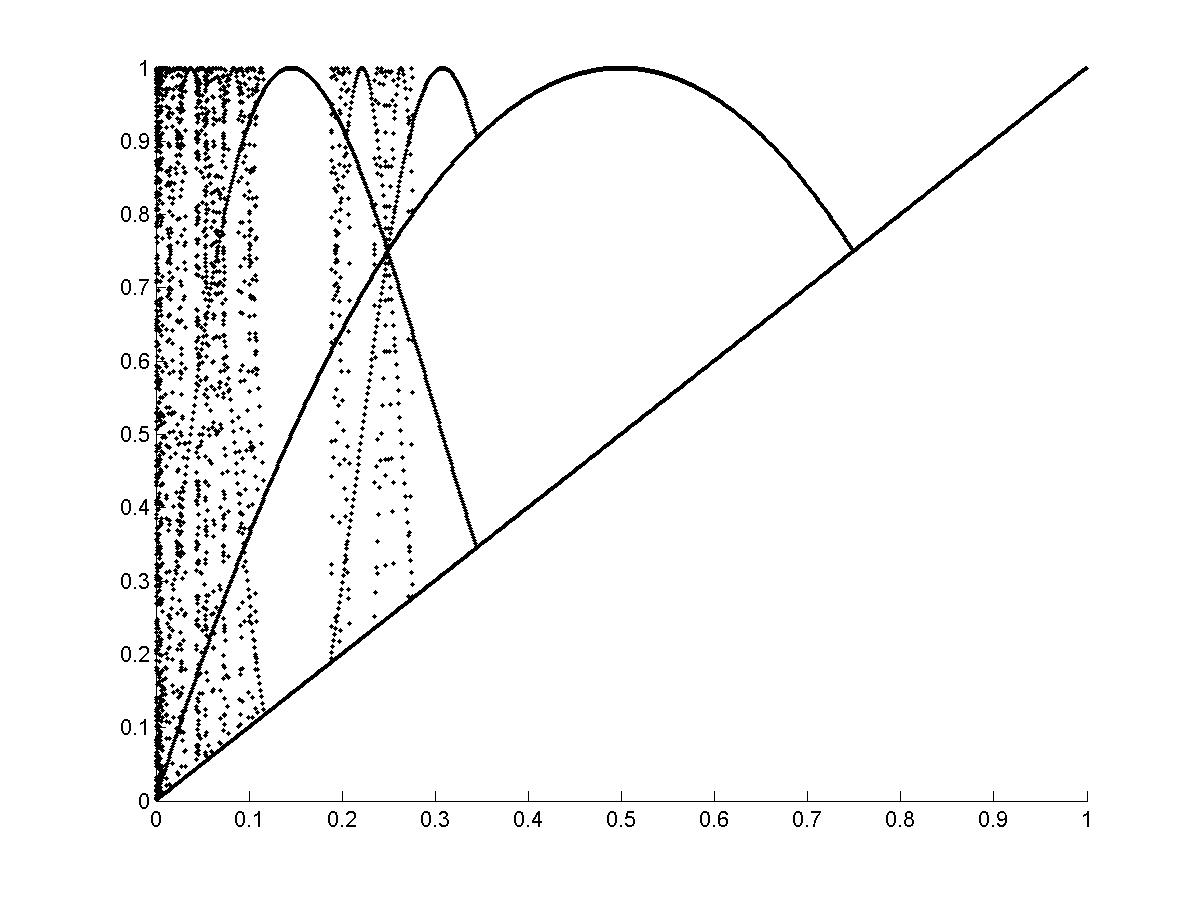
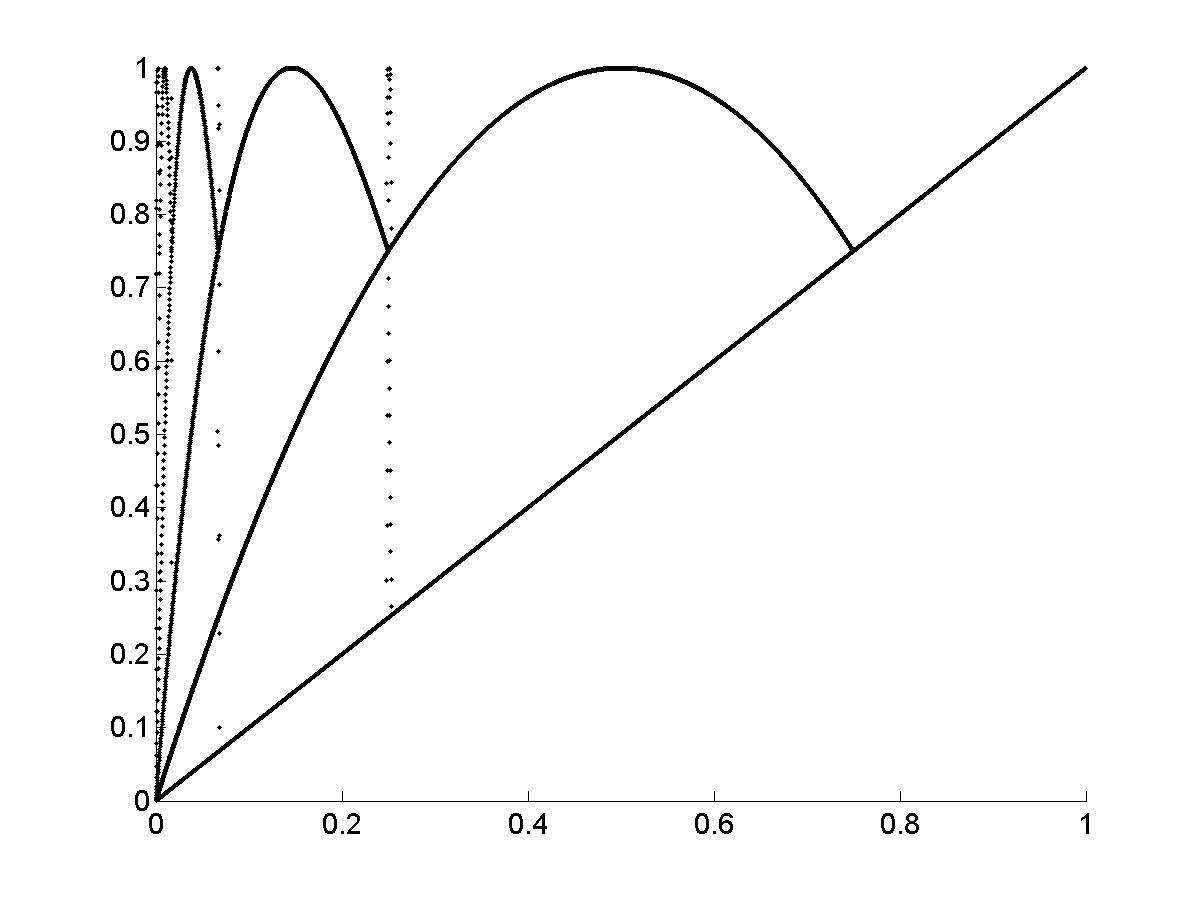
Двухзонное отображение выбрано для исследования, так как его ЛВ и ОПР обладают симметрией. На рис. 6 нанесены несколько линий возврата, хорошо видна симметрия. Сравнение рис. 6а и рис.6б говорит о том, что симметрия сохраняется при изменении масштаба. Рис. 5, 7 показывают, что n- кратные отображения и его повороты формируют ЛВ и ОПР. Рис. 8, 9, 12, 13, 16, 17 показывают, что траектории дискретных отображений независимо от вида функции при изменении высоты ступеньки d содержат элементы n-кратных отображений.

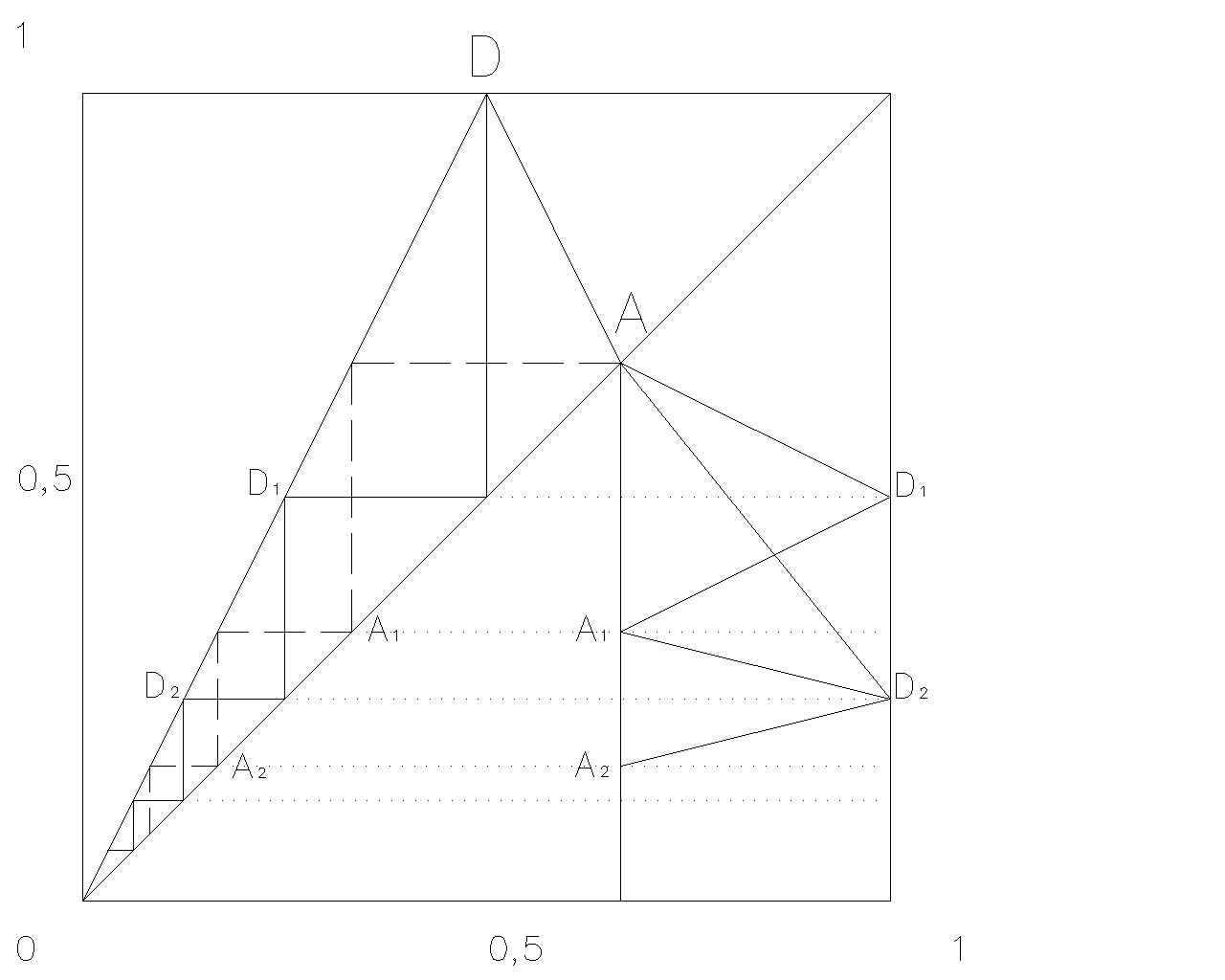
Рис.8. N-кратные отображения для ДДО ABC (DEFG – 2-кратное отображение, DD1D2D3H4- 3- кратное отображенение, DHH1H2H3H4 – 4 – кратное отображение, DP1P2P3H4 - 5 – кратное отображение, DN1N2N3H4 - 6 – кратное отображение).

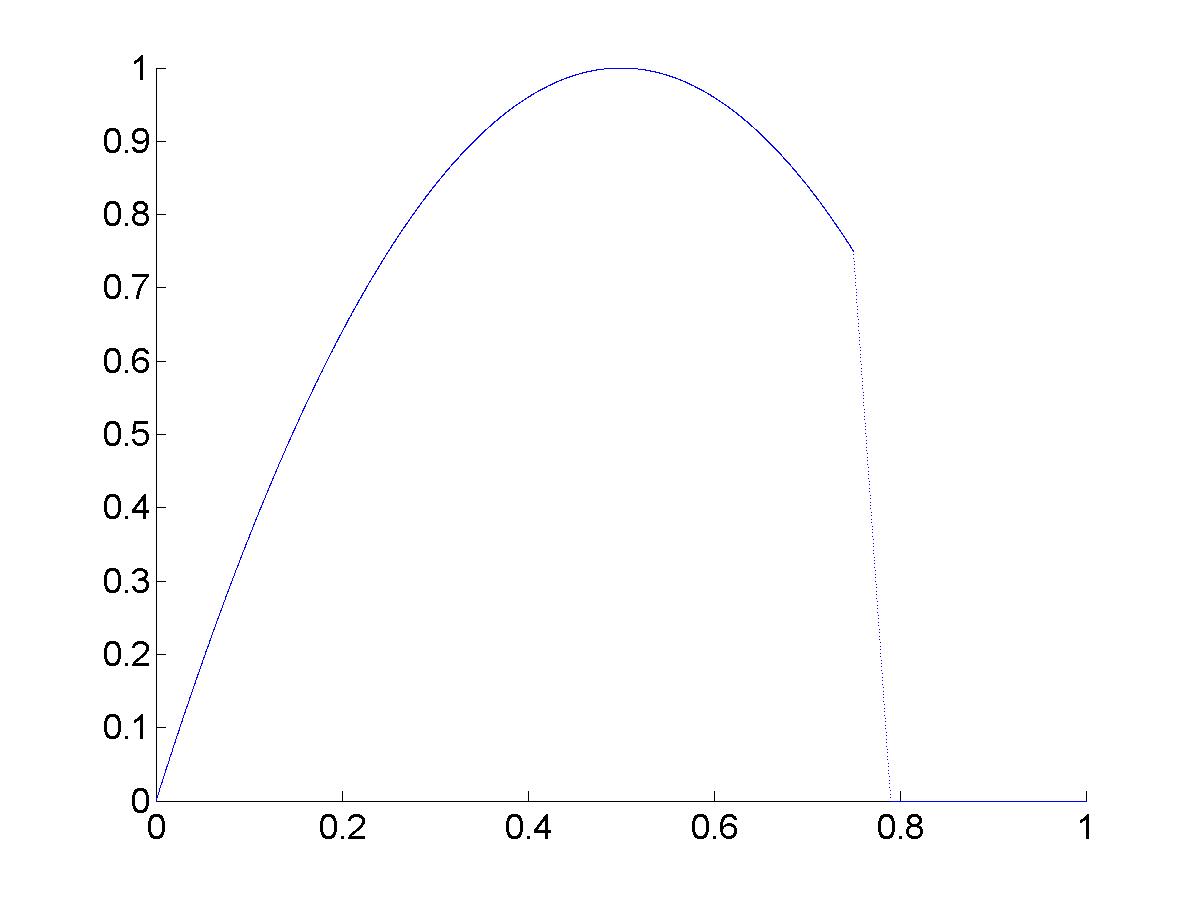
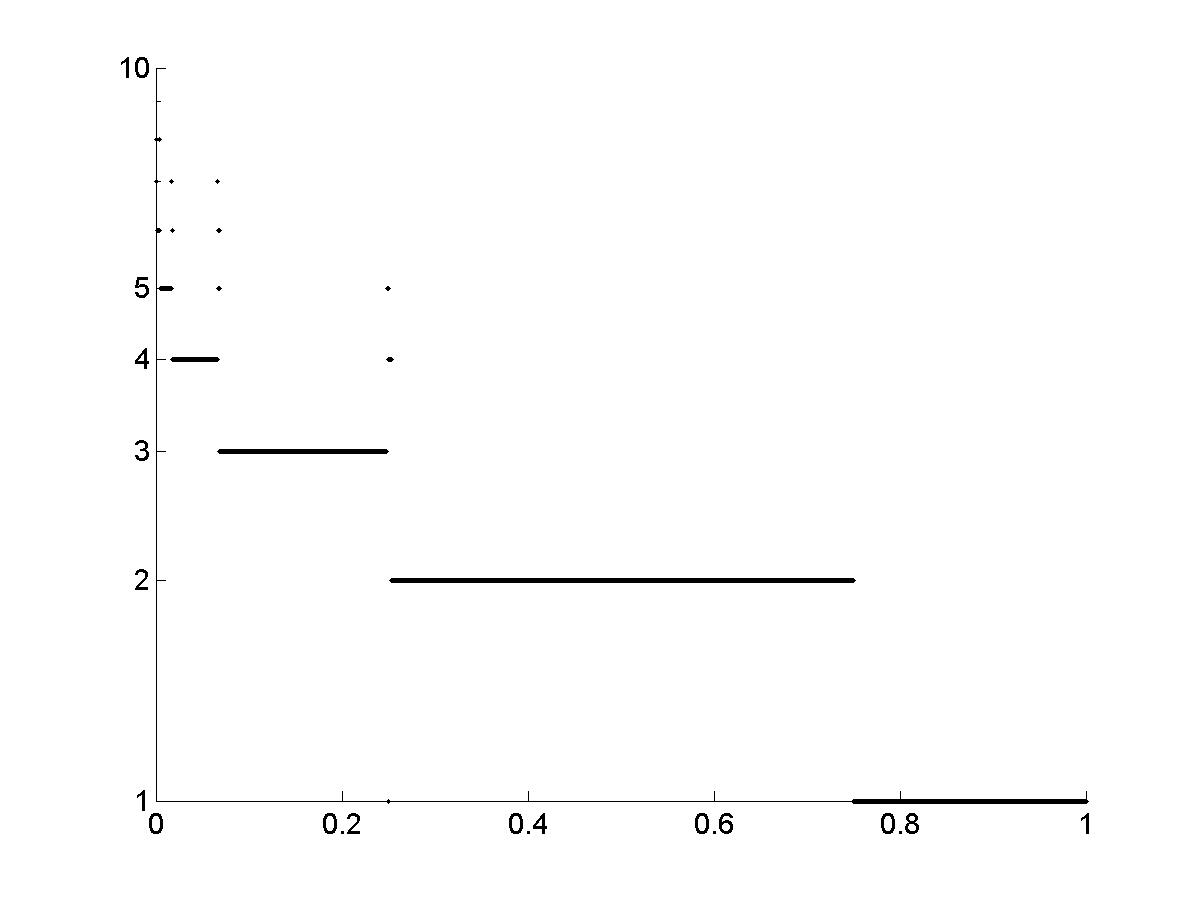
Можно избавиться от зон со сложными режимами (чёрные полосы) и добиться изменения периодов цикла последовательно в порядке натурального ряда, если ступеньку после точки равновесия опускать не от исходной функции, а от прямой, близкой к вертикальной. Пример такой функции изображён на рис.18. Рис. 10, 11, 14, 15, 19, 20 демонстрируют изменение периодов циклов в порядке натурального ряда при полном исчезновении зон со сложными режимами.

Отметим, что наличие ступеньки нарушает условие обычно налагаемые на производную Щварца. Но вне зависимости от этого порядок натурального ряда присутствует для всех функций и сценариев. Он связан с тем, что траектория за положением равновесия не может находиться два такта подряд; она служит своего рода "отражателем", фактически задавая начальные значения для движения траектории по левой части функции, В левой части траектория может находиться определенное число тактов. Количество тактов пребывания траектории в левой части определяется расположением прообразов положения равновесия F^-n(A). В сценариях «опускания ступеньки» мы последовательно переходим из одной зоны (F^-n-1(A), F^-n(A)) в другую. При этом количество тактов пребывания в левой части изменяется в порядке натурального ряда.

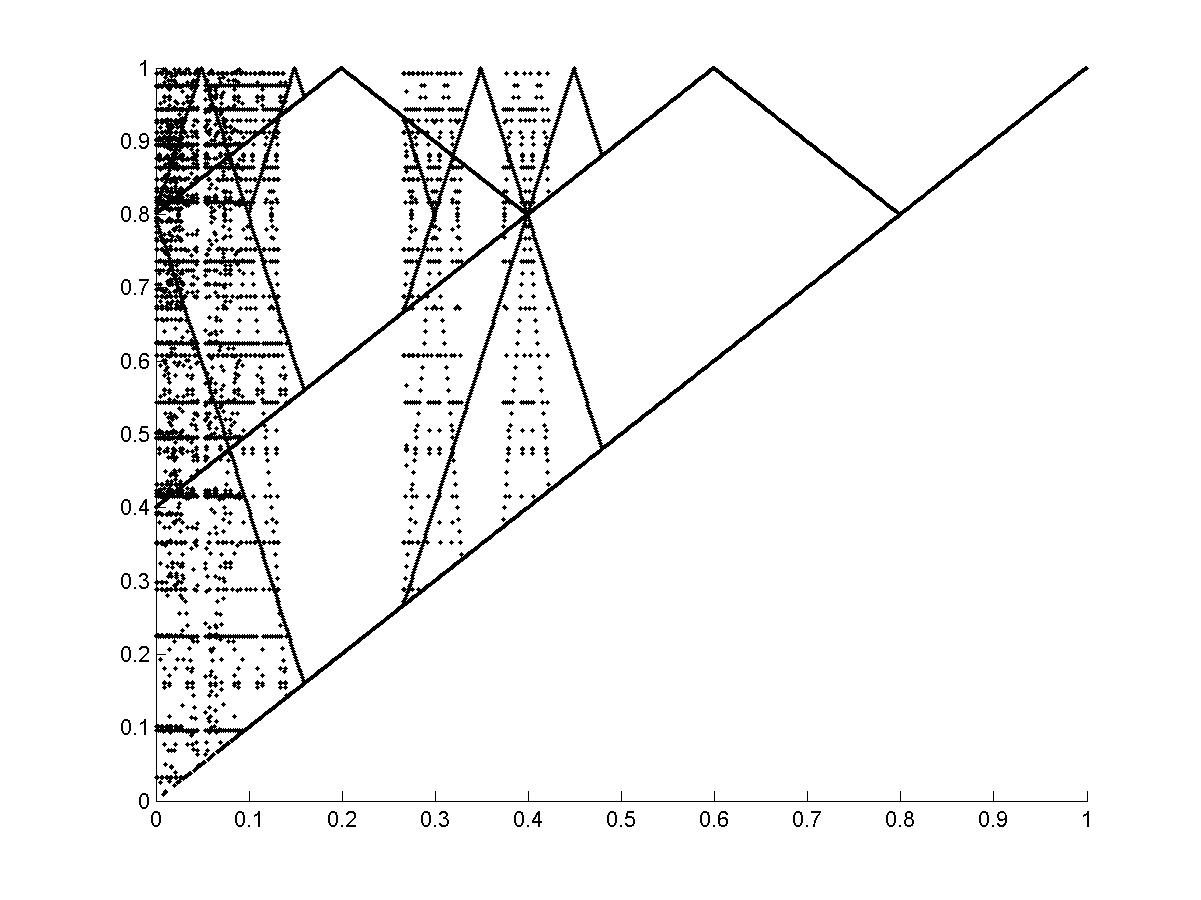
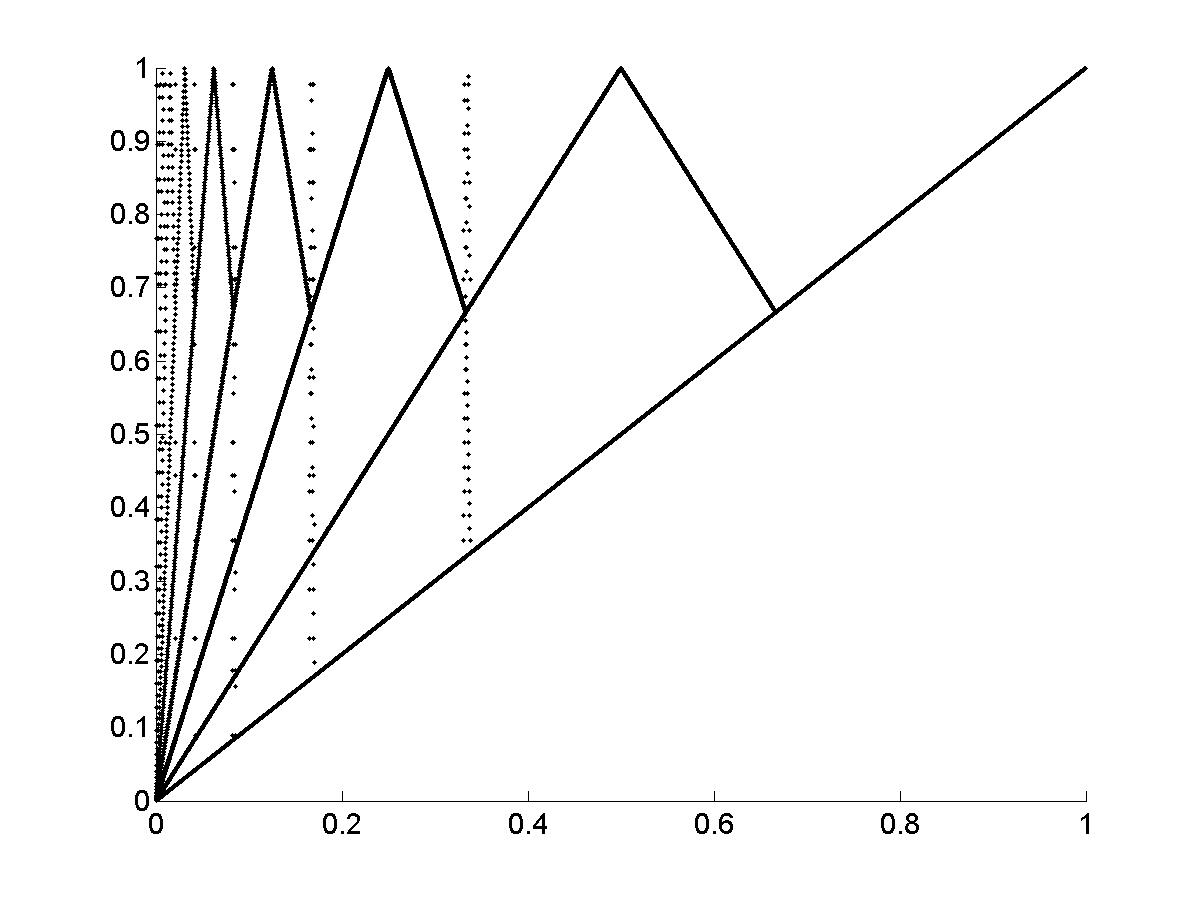
Рис.9. Результаты вычислительного эксперимента с ДДО, дополненным ступенькой при изменении высоты ступеньки d (0<d<1). Зависимость траекторий расчётной модели (по вертикали) от высоты ступеньки d (по горизонтали).

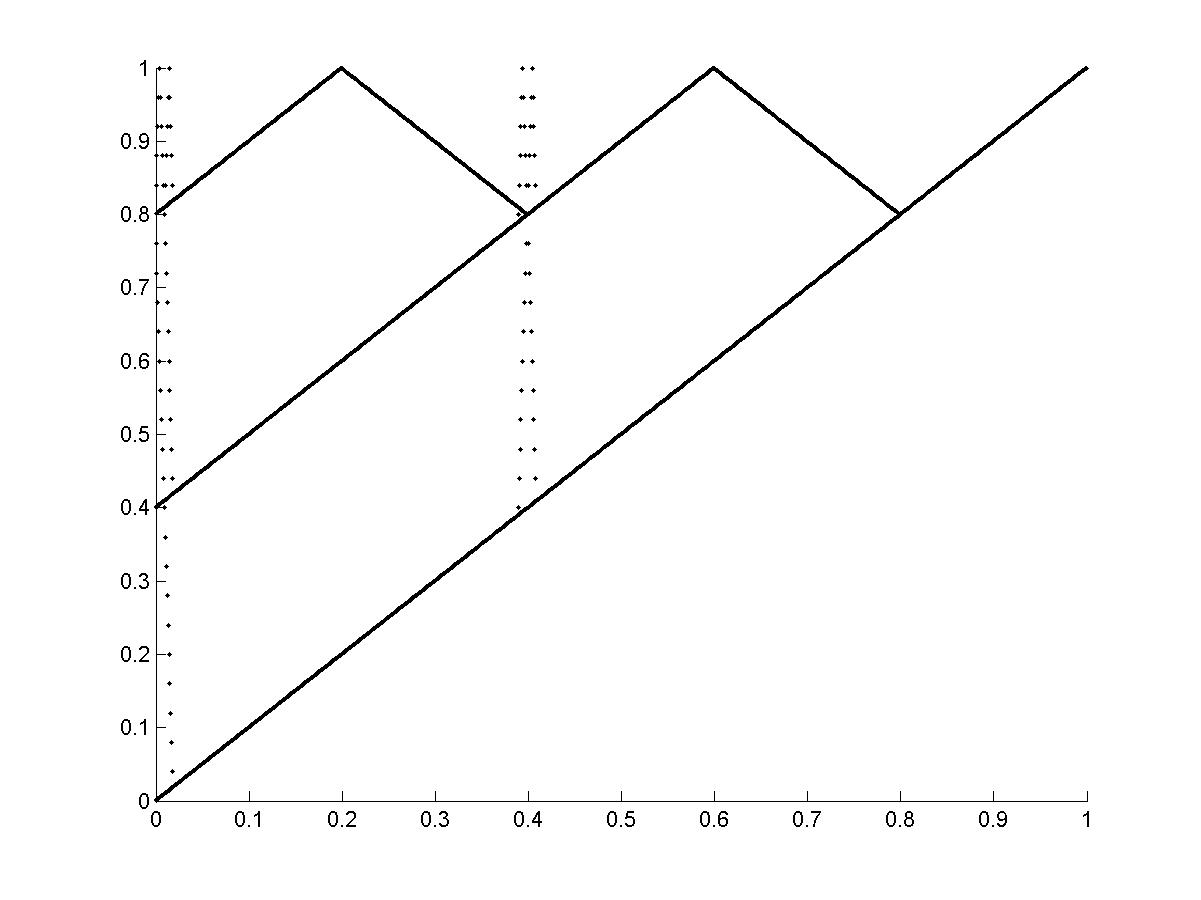
Рис.10. Результаты вычислительного эксперимента с ДДО, дополненным ступенькой при изменении высоты ступеньки d (0<d<1). Зависимость траекторий расчётной модели (по вертикали) от высоты ступеньки d (по горизонтали). При этом после точки равновесия ступенька опускается по прямой близкой к вертикали.

Проявление порядка натурального ряда можно рассмотреть и в популярном исследовании логистического отображения. Но из-за «пологости функции» переходная зона (со сложными режимами) много шире зон стабильности.

Остановимся еще на одном аспекте, на связи результатов вычислительных экспериментов с логистическим уравнением и теоремой Шарковского. В вычислительном эксперименте наблюдаются установившиеся, повторяющиеся траектории – или с определенным периодом, или квазистохастические, «закрашивающие определенные области». В теореме Шарковского не обсуждается устойчивость траекторий. Связь получения удвоения периода чисто внешне совпадает с этой частью Теоремы. Как показывает детальное исследование, (в частности построение Линий возврата (см. ниже соответствующие рисунки)) в случае, когда положение равновесия неустойчиво и при этом , где e>0, в любой окрестности положения равновесия существуют четные циклы с периодом больше любого наперед заданного числа. В рассматриваемых примерах они все неустойчивы, амплитуда их близка к нулю. Поэтому они не наблюдаемы в вычислительных экспериментах.

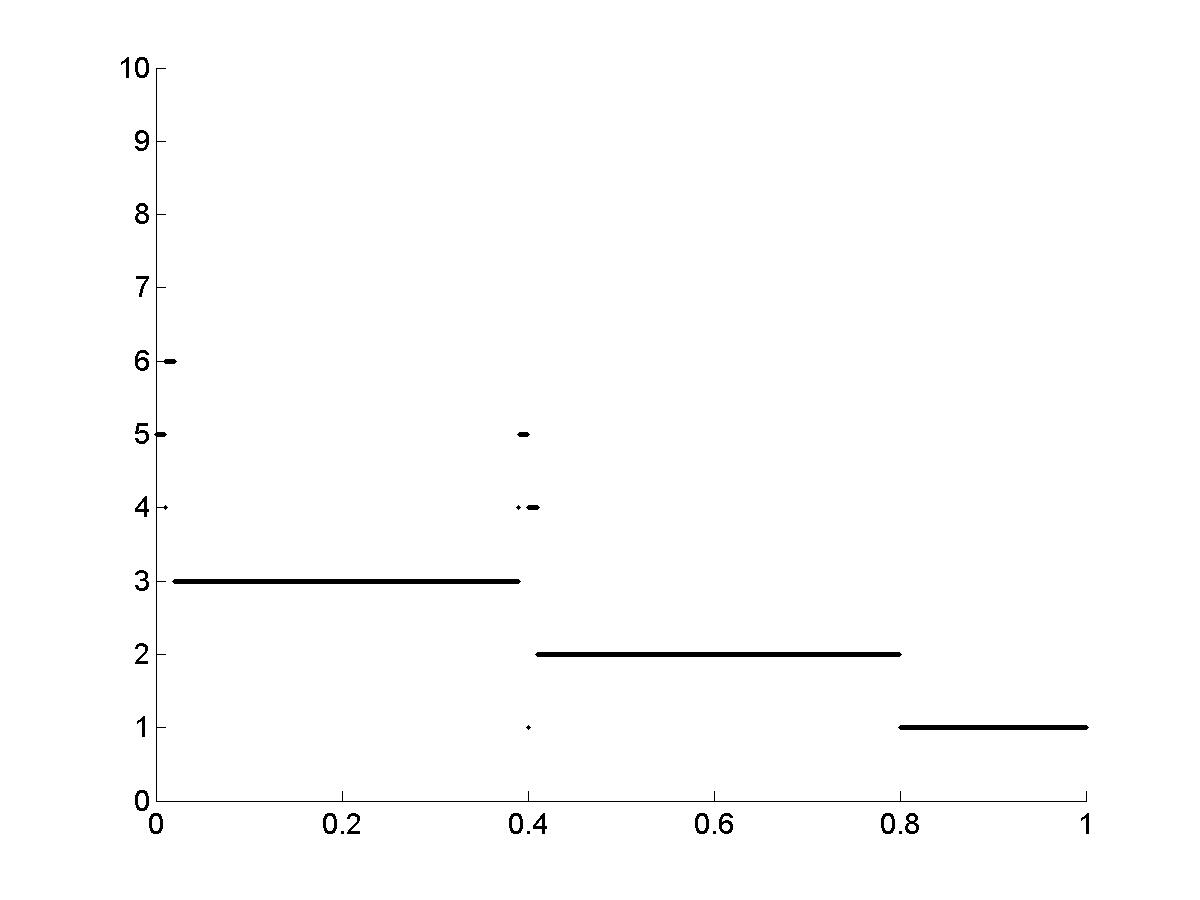
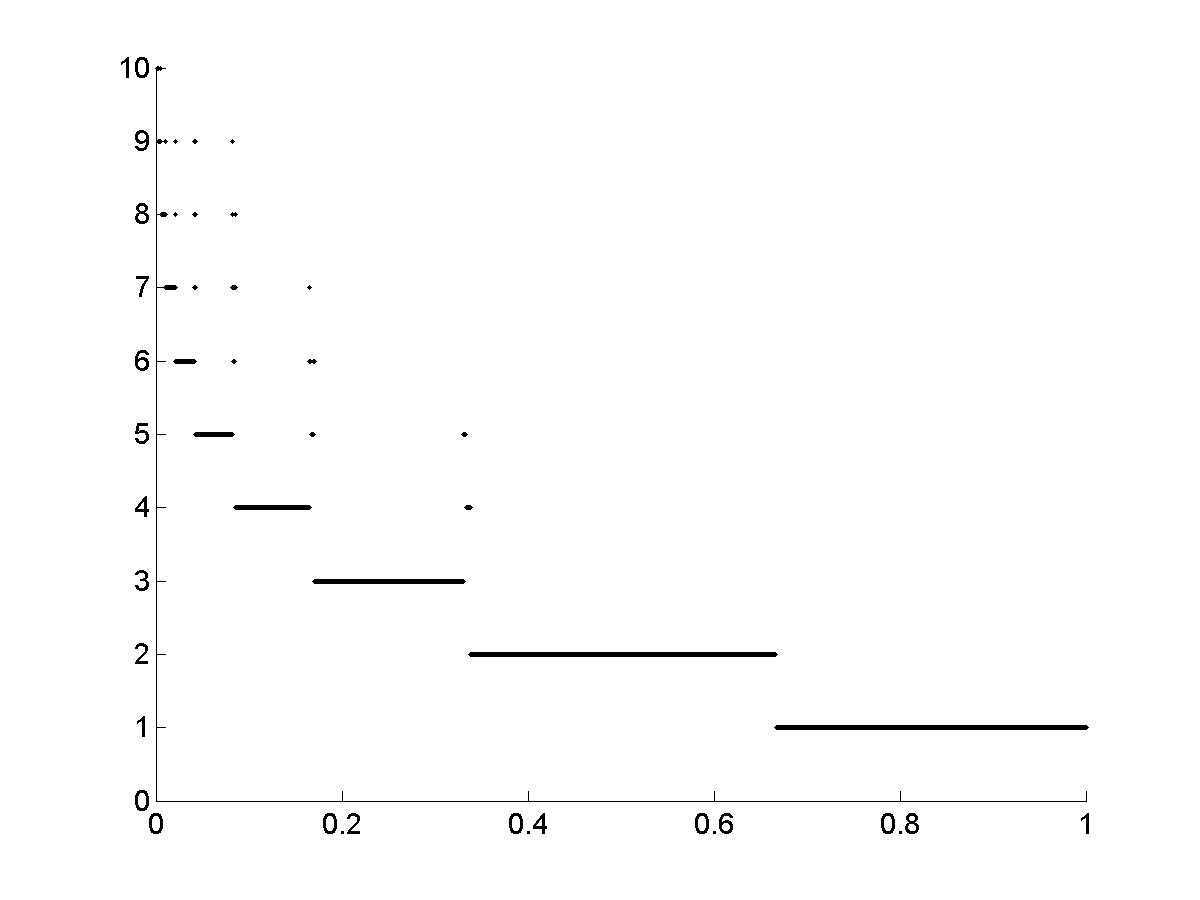
Рис.11. Зависимость периода цикла от высоты ступеньки d для вычислительного эксперимента рис.10.

Рис.12. N-кратные отображения для треугольного отображения.

Рис.13. Результаты вычислительного эксперимента с треугольным отображением, дополненным ступенькой при изменении высоты ступеньки d (0<d<1). Зависимость траекторий расчётной модели (по вертикали) от высоты ступеньки d (по горизонтали).

Рис.14. Результаты вычислительного эксперимента с треугольным отображением, дополненным ступенькой при изменении высоты ступеньки d (0<d<1). Зависимость траекторий расчётной модели (по вертикали) от высоты ступеньки d (по горизонтали). При этом после точки равновесия ступенька опускается по прямой близкой к вертикали.

Рис.15. Зависимость периода цикла от высоты ступеньки d для вычислительного эксперимента рис.14.

Рис.16. N-кратные отображения для логистического отображения.

Рис.17. Результаты вычислительного эксперимента с логистическим отображением, дополненным ступенькой при изменении высоты ступеньки d (0<d<1). Зависимость траекторий расчётной модели (по вертикали) от высоты ступеньки d (по горизонтали).

Рис.18. Логистическая функция, дополненная прямой близкой к вертикали после точки равновесия.

Рис.19. Результаты вычислительного эксперимента с логистическим отображением, дополненным ступенькой при изменении высоты ступеньки d (0<d<1). Зависимость траекторий расчётной модели (по вертикали) от высоты ступеньки d (по горизонтали). При этом после точки равновесия ступенька опускается по прямой близкой к вертикали.

Рис.20. Зависимость периода цикла от высоты ступеньки d для вычислительного эксперимента рис.19.

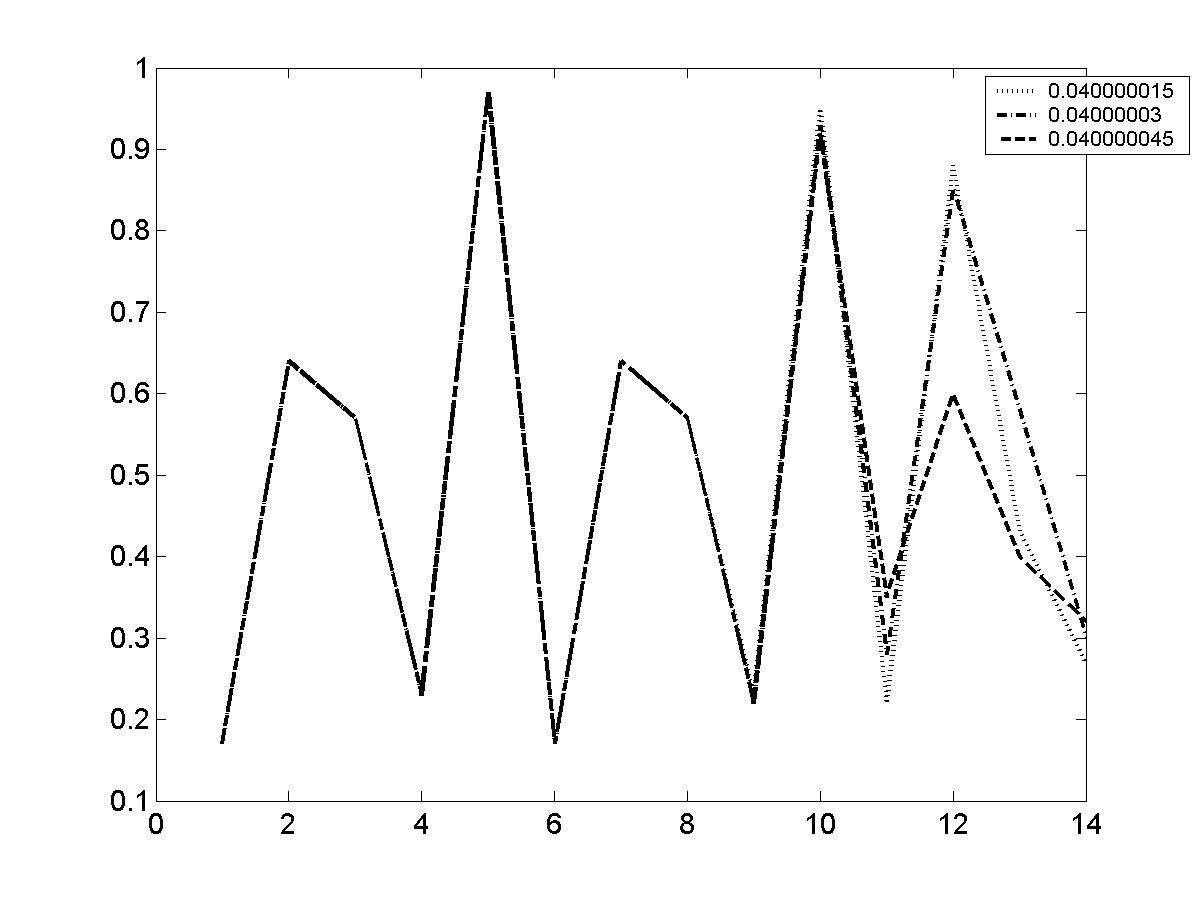
Рис.21а. Координаты линий возврата (с 1 по 14) при трёх близких, но разных исходных значениях для ДДО.

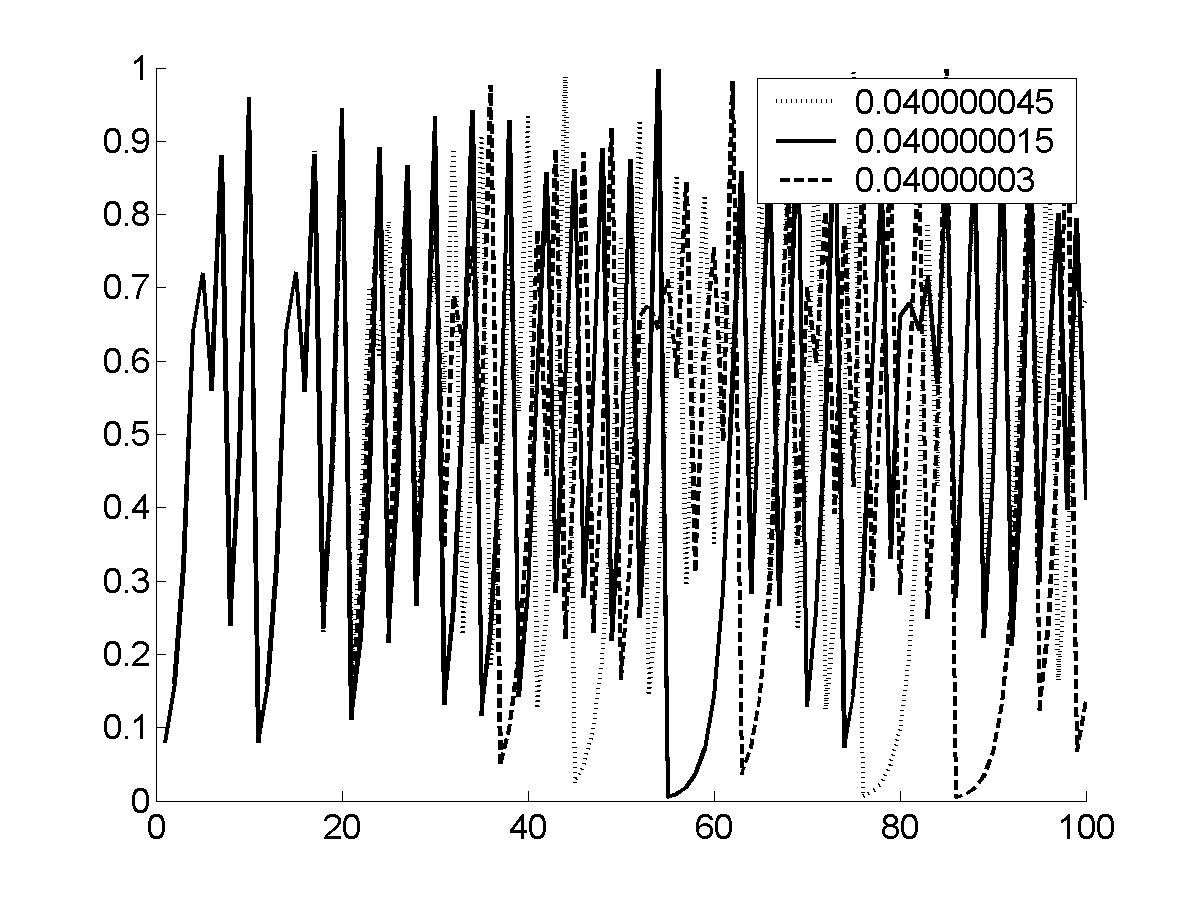
Рис.21б. . Времянные ряды в трех близких точках для ДДО. Временные ряды соотвествуют ЛВ рис. 21a.

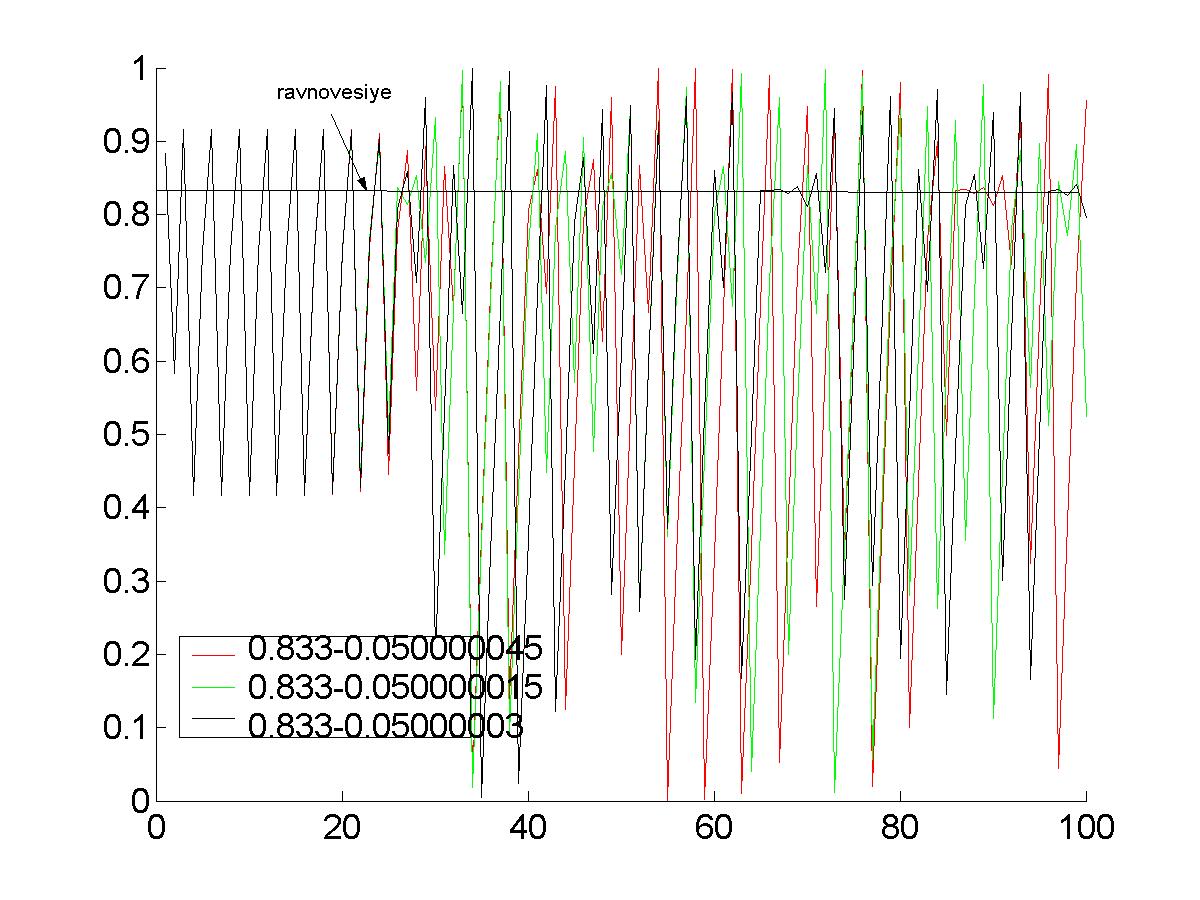
На рис.21a изображены координаты линий возврата (с 1 по 14) при трёх близких, но разных исходных значениях для ДДО. Видно, что координаты для первых 11 линий совпадают (а в окресности периодической точки (рис.24а) несколько раз координата сохраняется примерно постоянной, что изображено горизонтальной прямой), это отражено на эволюции временных рядов не зависимо от вида функции дискретного отображения (см. рис. 21б, 22, 23, 24б).

Рис.22. Времянные ряды для в трех близких точках для треугольного отображения.

Рис.23. Времянные ряды для в трех близких точках для логистического отображения.

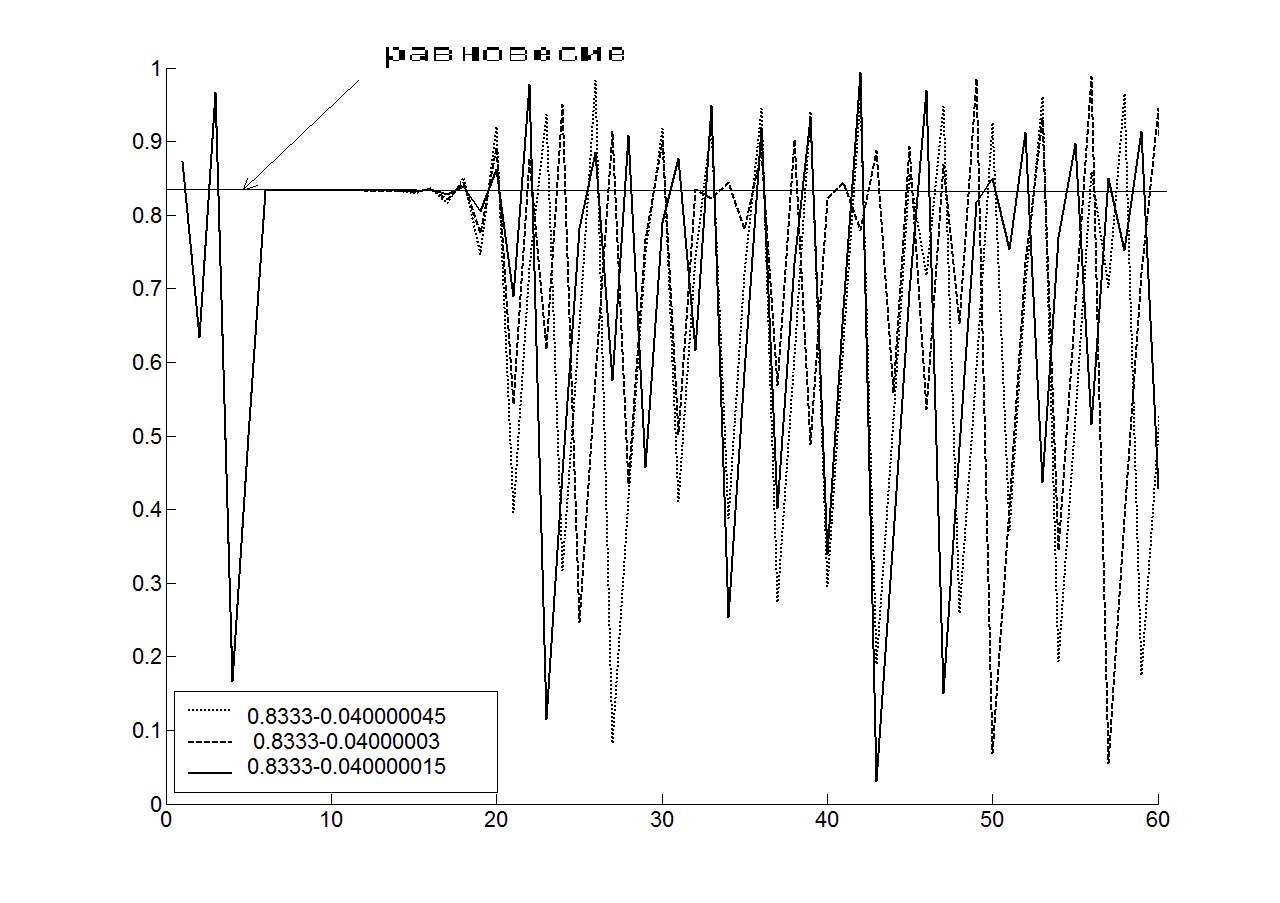
Рис.24a. Координаты линий возврата (с 1 по 14) при трёх близких, но разных исходных значениях для ДДО в окресности периодической точки.

Рис.21б. . Времянные ряды в трех близких точках для ДДО. Временные ряды соотвествуют ЛВ рис. 24a.

Рис.25. Исходное отображение (0DAD2 ), его ЛВ1, это простейшее отображение, которое содержит цикл периода три, а также циклы любой длины.

Рис.26. ОПР для исходного отображения с рис. 25, линия ЛВ1 для ОПР, показано, как формируются циклы любой длины

На рис.25 изображено простейшее отображение, содержащее цикл периода три, он образуется, если из правой точки D₂ начать двигаться по лестнице Ламерея. ОПР помогает определить циклы более высоких порядков. Поясним алгоритм построения циклов высоких порядков. Находится точка пересечения ОПР и ЛВ1 (рис.26), далее определяется, какой зоне на диагонали соответствует эта точка, например, область от точки А до точки А₁ называется зоной двойки, область от точки А₁ до точки А₂ называется зоной тройки и т.д. Номер зоны определяет период цикла, проходящего через данную точку. Далее фиксируется абсцисса выбранной точки и ставится новая точка на исходном отображении (рис.25), соответствующая данной абсциссе. Истинной период новой точки на рис. 25 складывается из периода точки на рис.25 и периода точки на рис.26.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 07-01-00473-а, проект 08-07-00118-a).