§5. Асимптотические направления лвп

Прямая имеет асимптотическое направление к ЛВП, когда

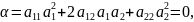
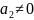координаты направляющего вектора прямой, тогда они сразу не могут равняться нулю. Пусть , тогда поделим на

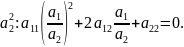
Обозначим 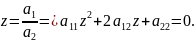Количество решений квадратного уравнения зависит от дискриминанта

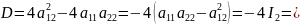Линии эллиптического типа не имеют асимптотических направлений. Линии параболического типа имеют одно асимптотическое направление. Линии гиперболического типа имеют два асимптотических направлений.

§6. Асимптоты лвп

Кроме того, что должно выполняться, что .

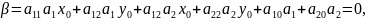где 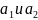находятся из условия , а координаты некоторой точки, принадлежащей асимптоте.

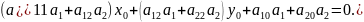
Будем считать точку 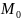произвольной точкой 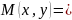будем определять асимптоту (прямую), если коэффициенты при 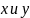одновременно не равны нулю.

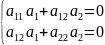Если же , где 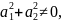то система имеет бесчисленное множество решений 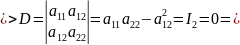линии параболического типа не имеют асимптот.

У линии гиперболического типа две асимптоты.

У линий эллиптического типа асимптот нет, так как нет асимптотических направлений.

Задача. Найти векторы асимптотического направления для ЛВП, заданной уравнением 2х² + 3ху + у² – 2х + у = 0. Написать уравнение асимптот, если они существуют.

Решение.1)Находятся векторы асимптотического направления, используя уравнение (4). Для этого составляется квадратное уравнение 2k² + 3k + 1 = 0. Отсюда 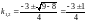, или k₁= –1, k₂= .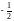

Квадратное уравнение имеет два решения. Поэтому у данной ЛВП два асимптотических направления и две асимптоты, так как J₂<0. Найдем асимптотические направления:

а) . Отсюда а₁= – а₂.

б) 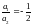. Отсюда а₂ = –2а₁.

2) Уравнения асимптот можно найти в виде (6):

а)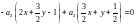 , т.к. а₂ ≠ 0, то 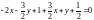или х + у – 3 =0.

б) .

Так как а₁≠0, то 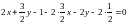или 2х + у + 4 =0.

Ответ: 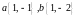, x + y – 3 = 0 и 2x + y + 4 = 0.■

§7. Диаметры лвп

Определение. Диаметром ЛВП сопряженных к вектору 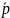, называется множество всех середин хорд ЛВП, параллельных вектору

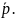
Пусть дана ЛВП уравнением (*) и вектор не асимптотического направления .

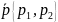Пусть 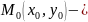является серединой хорды, параллельной вектору . Так как имеет не асимптотическое направление, то эта хорда пересекается с ЛВП в двух точках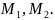

Уравнение хорды:

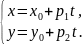
При ;

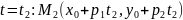
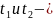решения уравнения

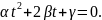
Точка должна являться серединой отрезка

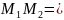
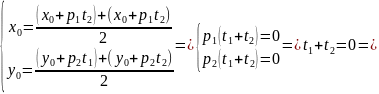
По теореме Виета

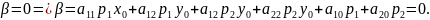
Так как 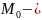произвольная точка, принадлежащая диаметру, то будем вместе брать точку .

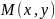Следовательно, это уравнение диаметра.

Известно, что

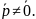
Рассмотрим выражение 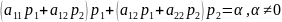, так как не имеет асимптотического направления.

Следовательно, коэффициенты в скобках не могут одновременно равны нулю, тогда уравнение диаметра является уравнением первой степени, то есть всегда определяет прямую линию.

Замечание 1. Если у ЛВП имеется центр

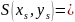
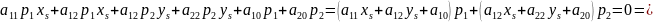
если ЛВП имеет центр, то любой диаметр проходит через центр.

Замечание 2. Если у ЛВП являются линий параболического типа, то 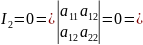существует

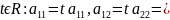
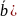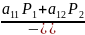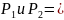если взять направляющий вектор диаметра , то отношение и оно не зависит от вектор 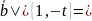все диаметры линий параболического типа параллельны.

Замечание 3. Направляющий вектор диаметра 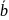и вектор называются сопряженными 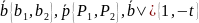с другой стороны

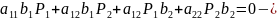условие сопряженности двух векторов относительно ЛВП.

Задача. Найти диаметр кривой x² – 2xy + 4y² – 6x+2y – 7 = 0, сопряженный: а) оси Оy, б) оси Ох.

Решение. а) В качестве вектора , сопряженного с искомым диаметром, можно взять вектор 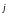{0, 1}, то есть 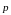{0,1}. Уравнение диаметра будем искать в виде:

p₁ (a₁₁x + a₁₂y + a₁₀) + p₂(a₁₂x + a₂₂y + a₂₀) = 0, где 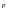{p₁, p₂}.

Тогда учитывая, что p₁ = 0, p₂ = 1, получим

0(x – y – 3) + 1 (– x + 4y + 1) = 0, то есть уравнение диаметра будет иметь вид x – 4y – 1 = 0 .

б) {1, 0}, тогда 1(x – y – 3) + 0 (–x + 4y + 1) = 0 или x – y – 3 = 0.■