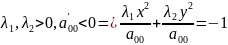ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ
Государственное образовательное учреждение высшего профессионального образования
«Арзамасский государственный педагогический институт имени А.П. Гайдара»
Кафедра математики, теории и методики обучения математике
Корнева А.А., студентка
4 курса очного отделения
физико-математического
факультета
КУРСОВАЯ РАБОТА
Общая теория кривых второго порядка
Научный руководитель:
к. п. н. доцент Фомина Н.И.
Арзамас
2011
С О Д Е Р Ж А Н И Е
ВВЕДЕНИЕ ……………………………………………………….…….….…..3
§1.Общее уравнение линии второго порядка и его приведение
к каноническому виду…………………….…………….………………….….4
§2. Центр ЛВП………………………………………………………….......…12
§3.Пересечение ЛВП с прямой…………………………………………..…..15
§4. Касательная к ЛВП……………………………………………………….16
§5. Асимптотические направления ЛВП…………………………………....18
§6. Асимптоты ЛВП………………………………………………………......19
§7. Диаметры ЛВП………………………………………………………….…21
§8. Главные направления…………………………………………………......23
ЗАКЛЮЧЕНИЕ …………………………………………………………........25
ЛИТЕРАТУРА…………………………………………………………….…..26
В В Е Д Е Н И Е
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Объектом исследования в работе являются кривые.
Предметом исследования стала теория кривых второго порядка.
Целью работы является рассмотреть общую теорию кривых второго порядка.
В работе были поставлены и решены следующие задачи:
– рассмотреть классификацию линий второго порядка, количество решений в результате пересечения линий второго порядка и прямой, линии эллиптического, гиперболического, параболического направлений и их количество асимптот;
– проанализировать преобразование общего уравнения линий второго порядка к каноническому виду;
– рассмотреть различные задачи на приведение уравнения к каноническому виду, нахождение центра кривой, заданной уравнением, нахождение диаметра кривой, поиск направлений линий второго порядка.
Работа имеет традиционную структуру и включает в себя введение, основную часть, состоящую из 8 параграфов, заключение и используемой литературы.
В работе представлены следующие определения: центра линий второго порядка, диаметра линий второго порядка, главное направление вектора.
§1. Общее уравнение линии второго порядка и его приведение к каноническому виду
Пусть
в прямоугольной системе координат
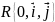 линия второго порядка (ЛВП) задана общим
уравнением
линия второго порядка (ЛВП) задана общим
уравнением
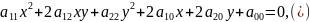
Если систему координат изменить, то уравнение ЛВП будут иметь ту же степень.
Для
того, чтобы уравнение
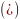 упростить,
нужно выбрать новую систему координат.
упростить,
нужно выбрать новую систему координат.
Пусть
коэффициент
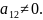
Найдем
такой угол поворота α системы координат
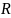 ,
что в новой системе координат
,
что в новой системе координат
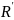 в уравнении ЛВП
коэффициент
в уравнении ЛВП
коэффициент
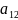 будет равен нулю.
будет равен нулю.
Формулы преобразования прямоугольной системы координат в следующие:
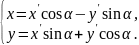
Подставим их в уравнение .
Получим
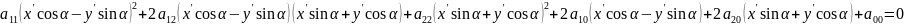 .
.
Сгруппируем
коэффициенты при
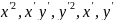 и свободном члене.
и свободном члене.
Получим:
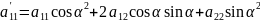
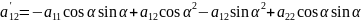
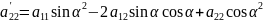
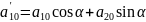
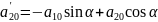
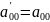
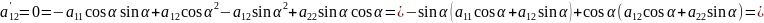
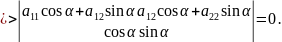
Определитель равен нулю, следовательно, его строки пропорциональны.
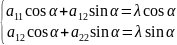 ,
,
λ – коэффициент пропорциональности.
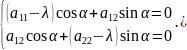
Из
системы
 можно определить
можно определить
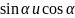 .
.
Система имеет бесчисленное множество решений, если главный определитель равен нулю, то есть
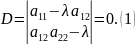
Уравнение
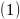 называется характеристическим уравнением
ЛВП.
называется характеристическим уравнением
ЛВП.
Раскроем определитель:
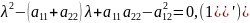
определим количество решений квадратного уравнения. Для этого посчитаем дискриминант
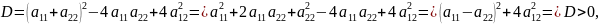
то
есть существует два решения
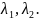
Замечание
1.
Величины
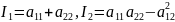 называются соответственно первым и
вторым инвариантом ЛВП.
называются соответственно первым и
вторым инвариантом ЛВП.
Они не изменяется при преобразовании системы координат.
Докажем
для
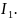
Действительно,
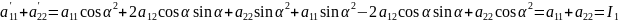
Из уравнений системы
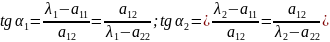 ,
,
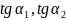 -
это угловые коэффициенты новой оси
-
это угловые коэффициенты новой оси
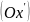 относительно
старой системы координат
относительно
старой системы координат
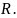
Замечание
2.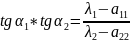 .
.
Докажем.
Из
уравнения
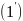 по теореме Виета имеем
по теореме Виета имеем
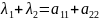 ,
,
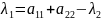 ,
,
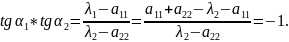
Углы
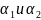 отличаются друг от друга на
отличаются друг от друга на
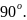
По
тангенсу
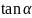 можно найти
можно найти
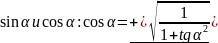 ;
;
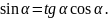
Подставив
найденные значения
в выражение для
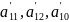 .
Избавимся от коэффициента
.
Избавимся от коэффициента
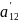 и
упростим общее уравнение ЛВП.
и
упростим общее уравнение ЛВП.
Замечание 3. Можно заменить
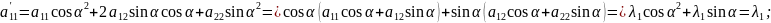
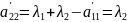 .
.
Установим, что поворачивая координатные оси, можно привести уравнение к виду:
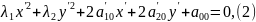
Если
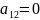 ,
то поворачивать систему координат не
нужно. К уравнению
,
то поворачивать систему координат не
нужно. К уравнению
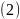 применяют параллельный перенос системы
координат.
применяют параллельный перенос системы
координат.
Рассмотрим два случая:
1).
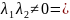
 .
.
Выделяем полный квадрат:
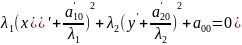 ,
,
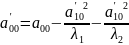 .
.
Произведем
параллельный перенос:
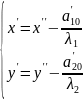
Получим
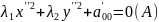
2).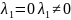
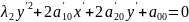 ,
,
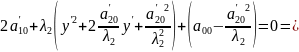
Если
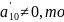
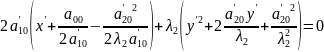 ,
,
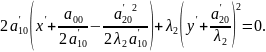
Обозначив
первую скобку за
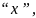 а вторую за
а вторую за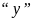 получим:
получим:
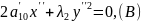
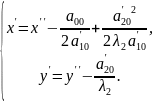
Установим, что при помощи выбора системы координат общее уравнение ЛВП можно привести к двум видам:
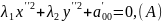
Эти
виды
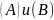 называются каноническими видами ЛВП.
называются каноническими видами ЛВП.
Классификация ЛВП.
Рассмотрим
вид
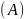 :
:
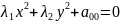
пусть
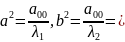
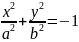 – мнимый
эллипс.
– мнимый
эллипс.
пусть
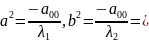
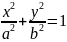 –
эллипс.
–
эллипс.
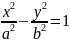 –
гипербола.
–
гипербола.
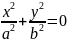 – это
уравнение определяет точку (0,0) или пару
мнимых пересекающихся прямых.
– это
уравнение определяет точку (0,0) или пару
мнимых пересекающихся прямых.
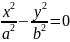 – это
уравнение пары пересекающихся прямых.
– это
уравнение пары пересекающихся прямых.
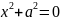 – пара
мнимых параллельных прямых.
– пара
мнимых параллельных прямых.
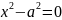 – пара
параллельных прямых.
– пара
параллельных прямых.
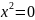 – пара
совпавших прямых.
– пара
совпавших прямых.
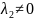 ,
так как это уравнение второй степени
,
так как это уравнение второй степени
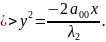
Пусть
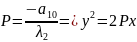 – это уравнение параболы.
– это уравнение параболы.
Все
кривые второго порядка в зависимости
от
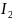 разделяются на 3 типа:
разделяются на 3 типа:
если
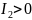 ,
то кривая эллиптического типа;
,
то кривая эллиптического типа;если
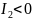 ,
то кривая гиперболического типа;
,
то кривая гиперболического типа;если
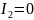 ,
то кривая параболического типа.
,
то кривая параболического типа.
Задача1.
Привести уравнение
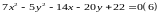 к каноническому виду. Сделать чертеж.
к каноническому виду. Сделать чертеж.
Решение.
В (1)
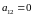 ,
поэтому его можно привести к каноническому
виду путем параллельного переноса
системы координат.
,
поэтому его можно привести к каноническому
виду путем параллельного переноса
системы координат.
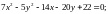
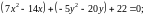
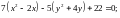
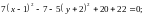
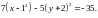
Обозначим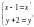 или
или
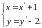
Геометрически
это означает параллельный перенос осей
координат в точку
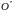 (1, –2). После параллельного переноса
получим
(1, –2). После параллельного переноса
получим
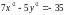 или
или
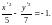 Это каноническое уравнение гиперболы
с действительной осью Оу.
Для построения изображаются старая и
новая системы координат. Затем от точки
Это каноническое уравнение гиперболы
с действительной осью Оу.
Для построения изображаются старая и
новая системы координат. Затем от точки
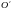 в обе стороны откладываются отрезки
в обе стороны откладываются отрезки
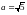 и
и
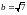 .
Получаются вершины гиперболы, лежащие
на оси Oу.
Можно для уточнения расположения
гиперболы найти точки её пересечения
со старыми осями координат.
.
Получаются вершины гиперболы, лежащие
на оси Oу.
Можно для уточнения расположения
гиперболы найти точки её пересечения
со старыми осями координат.
Если
х
= 0, то
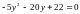 или
или
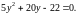 Отсюда
Отсюда
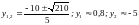 .Строятся
точки В1(0;
0,8) и В2(0;
–5) (рис.35). Если у
= 0,
то
.Строятся
точки В1(0;
0,8) и В2(0;
–5) (рис.35). Если у
= 0,
то
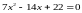 .
Так как
.
Так как
 ,
то D
< 0, поэтому действительных корней нет,
то есть с осью Ох
гипербола не пересекается. Для уточнения
изображения гиперболы полезно построить
её асимптоты. Уравнения асимптот данной
гиперболы в новой системе координат
имеют вид
,
то D
< 0, поэтому действительных корней нет,
то есть с осью Ох
гипербола не пересекается. Для уточнения
изображения гиперболы полезно построить
её асимптоты. Уравнения асимптот данной
гиперболы в новой системе координат
имеют вид
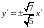 .
■
.
■
Задача 2. Привести к каноническому виду уравнение
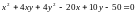 .
Определить вид линии второго порядка,
записать формулы преобразования системы
координат.
.
Определить вид линии второго порядка,
записать формулы преобразования системы
координат.
Р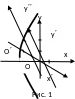 ешение.
а)
Составляется характеристическое
уравнение и находятся его решения
ешение.
а)
Составляется характеристическое
уравнение и находятся его решения
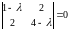 .
После раскрытия
.
После раскрытия
определителя
получается

или
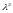 – 5
– 5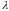 = 0,
= 0,
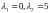 .
.
б) Далее ищется tgβ, а по нему sinβ и cosβ,
где β – угол поворота осей координат
относительно оси Ох.
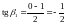 ,
,
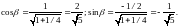

в)
Записываются формулы поворота осей на
угол β:
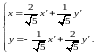
г) Преобразуется линейная часть уравнения
 д)
Записывается уравнение ЛВП после
поворота осей координат
д)
Записывается уравнение ЛВП после
поворота осей координат
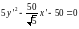 или
или
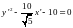 .
Отсюда:
.
Отсюда:
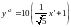 или
или
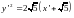 .
После применения параллельного переноса
по формулам
.
После применения параллельного переноса
по формулам
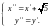 ,
получается уравнение параболы
,
получается уравнение параболы
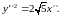
е) Для построения линии необходимо изобразить старую и новую системы координат. Затем, как и в предыдущем примере, построить линию в новой системе координат, используя каноническое уравнение этой линии (рис.1).