§2. Центр лвп

Определение. Центром ЛВП называется центр симметрии этой линии.

Пусть дана ЛВП

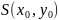Возьмем произвольную точку . Предположим, что эта линия имеет центр . Это означает, что к ЛВП принадлежит точка 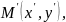симметричная точка 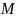относительно

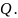
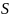– середина отрезка

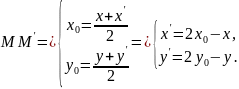
Точка

.

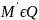
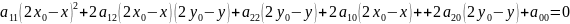
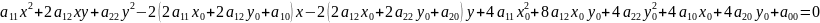Из этого уравнения вычтем , получим

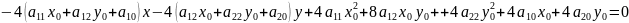
Далее

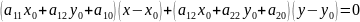
Это уравнение выполняется для любых 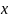и коэффициенты уравнения должны быть равны нулю, т.е.

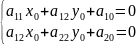
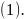
Из системы можно найти координаты центра. Количество решений системы зависит от определителя:

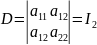
Если , система имеет единственное решение, это значит, что линии эллиптического и гиперболического типа имеют единственный центр, т.к. для линий эллиптического и гиперболического типов

Если 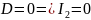. Следовательно, для линий параболического типа необходимо рассмотреть основную и расширенную матрицы.

Расширенная матрица

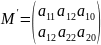
Рассмотрим линии

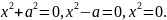
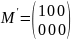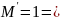Для них . Следовательно эти линии имеют бесчисленное множество.

Для параболы

Следовательно, система 1 не будет иметь решения. Следовательно, парабола центра не имеет.

Теорема. Для того, чтобы начало координат было центром ЛВП необходимо и достаточно, чтобы коэффициенты

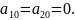
Доказательство:

1. Пусть

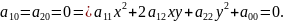
Если для любой 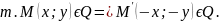Но 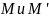симметричны относительно начала координат. Так как произвольная точка, то начало координат – центр ЛВП.

2. Пусть 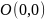– центр симметрии ЛВП. Если

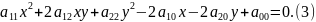
Вычтем из 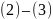равенство:

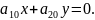
Последнее условие выполняется для любых

Вывод. При поведение общего уравнения ЛВП к каноническому виду осуществляется параллельный перенос начала координат в центр ЛВП.

Задача. Найти центр кривой, заданной уравнением

2x² + 5xy + 2y² – 6x – 3y – 8 = 0.

Решение. Составим систему уравнений(2) и решим её

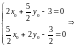
Отсюда y₀ = 2, x₀ = –1. Точка С(–1, 2) является центром кривой. ■

§3. Пересечение лвп с прямой

Пусть дана ЛВП уравнением

и прямая

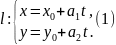
Подставим в :

.

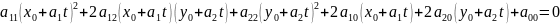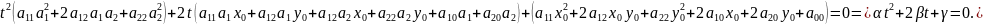
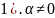. Число решений уравнения зависит от дискриминанта .

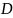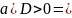прямая и кривая второго порядка пересекаются в двух действительных точках. В этом случае прямая называется секущей.

Прямая пересекается с кривой в двух совпавших точках. Прямая называется касательной к ЛВП. Еще касательной может называться прямая, которая целиком принадлежит ЛВП, то есть когда линия распадается на две прямые.

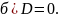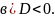Прямая пересекается с ЛВП в двух мнимых точках.

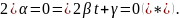Когда 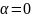, то говорят, что прямая имеет асимптотическое направление относительно ЛВП.

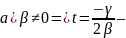имеется одна общая точка ψ.

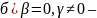нет общих точек.

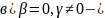прямая принадлежит ЛВП. Бесчисленное множество решений уравнения .

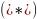В случае 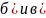прямая называется асимптотой ЛВП.

§4. Касательная к лвп

Пусть дана ЛВП уравнением и прямая

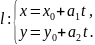
Обозначим ЛВП: .Пусть .

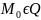Решая, совместно уравнение получим уравнение

.

Так как

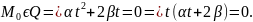
Для того чтобы прямая была касательной к ЛВП необходимо, чтобы два решения последнего уравнения совпали.

Так как 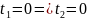(для этого нужно, чтобы ).

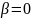Но

.

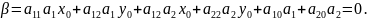
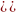Вектор 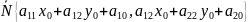внесли.

Следовательно, 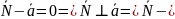вектор нормали касательной к ЛВП по вектору нормали и точке:

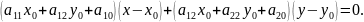
Это уравнение определяет касательную к кривой второго порядка.

Рассмотрим случай, когда оба коэффициента равны нулю:

, где 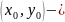центр ЛВП.

Следовательно, касательной к ЛВП не существует в центре этой линии в случая, когда центр лежит на этой линии. Это случай пары пересекающихся прямых.

Касательной к ЛВП в точке не существует.

.

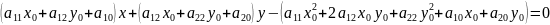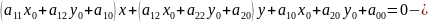это уравнение также можно использовать, как уравнение касательной к ЛВП.

Применим его к уравнению: (эллипс).

Касательная к эллипсу в точке .

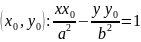Касательная к параболе

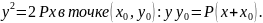
Задача. Через начало координат провести касательную к кривой

x² – 4xy + 4y² + 2x – 6y + 16 = 0.

Решение. Запишем уравнение касательной в виде (8), подставляя значения коэффициентов 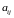из данного уравнения ЛВП:

(x₀ – 2y₀ + 1)x + ( 2x₀ + 4y₀ – 3)y + x₀ – 3у₀ + 16 = 0 (_*).

Так как точка О(0,0) принадлежит касательной, но не является точкой касания, то, подставляя в (_*) нули вместо х и у, получим

х₀ – 3y₀ + 16 = 0. Отсюда х₀ = 3y₀ – 16.

Точка касания (х₀, y₀) принадлежит данной линии. Поэтому, подставляя х₀ = 3y₀ – 16 в уравнение этой ЛВП, получим

(3y₀ – 16)² – 4(3y₀ – 16)y₀ + 4y₀² + 2(3y₀ – 16) – 6y₀ + 16 = 0.

Отсюда у₀₁ = 20, у₀₂ = 12. Тогда х₀₁ = 44, х₀₂ = 20.

Подставляя полученные координаты точек касания в (_*), найдем уравнения двух касательных к данной кривой, проходящих через начало координат 5x – 11y = 0, 3x – 5y = 0.■