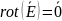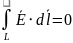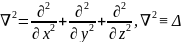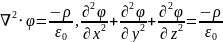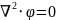- •Введение в электродинамику Свойства электрического заряда
- •Линии поля. Интегрирование (нахождение) линий поля
- •Сила Лоренца. Преобразования полей. Инварианты электромагнитного поля Сила Лоренца
- •Преобразования полей
- •Инвариантность электромагнитного поля
- •Напряженность и потенциал электрического поля неподвижных зарядов (точечных и непрерывно распределенных)
- •Электродвижущая сила
- •Магнитное поле движущегося заряда. Магнитный поток тока: закон Био и Савара
- •Циркуляция векторного поля
- •Уравнения Максвелла в интегральной форме Первое: теорема Гаусса для электростатики (обобщение закона Кулона)
- •Второе: закон Фарадея
- •Отступление
- •Четвертое
- •Уравнения Максвелла для магнитостатики
- •Уравнение электростатики диэлектриков
- •Намагниченность вещества. Уравнение магнитостатики в веществе
- •Граничные условия для электронных и магнитных полей.
- •Уравнения Максвелла для элекромагнитного поля в веществе
- •Система уравнений Максвелла в дифференциальной и интегральной форме с материальными уравнениями и граничными условиями
- •Электрические токи в проводниках. Электропроводность Классическая теория электропроводности. Законы Ома и Джоуля-Ленца в дифференциальной форме
- •Законы Ома и Джоуля-Ленца в интегральной форме
- •Законы (правила) Кирхгофа
- •Электромагнитная индукция Закон Фарадея. Электромагнитная индукция в неподвижных и подвижных проводниках. Токи Фуко Закон Фарадея
- •Электромагнитная индукция в подвижных и неподвижных проводниках
- •Токи Фуко
- •Самоиндукция и взаимоиндукция Коэффициент самоиндукции и взаимоиндукции
- •Явление взаимоиндукции и самоиндукции. Трансформаторы
Второе: закон Фарадея
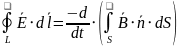
Циркуляция вектора напряженности электрического поля по какому-либо замкнутому контуру равна (со знаком «-») скорости изменения потока индукции магнитного поля через произвольную поверхность , опирающуюся на этот контур.
Какую бы шапку (поверхность , опирающуюся на контур ) мы не взяли, при одинаковых контурах будет одинаковая циркуляция. Векторы и находятся по правилу буравчика.
|
Закон Фарадея |
Третье
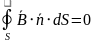
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Это – математическое выражение научного факта: в природе не существует элементарных магнитных зарядов.
Отступление
Первые
три уравнения надо читать справа налево:
следствие
 причина.
причина.
Четвертое
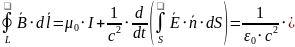
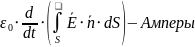
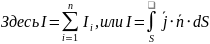
Циркуляция
индукции магнитного поля по замкнутому
контуру
равна
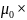 ток,
пронизывающий данный контур, плюс
ток,
пронизывающий данный контур, плюс
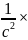 скорость
изменения потока напряженности
электрического поля через поверхность,
опирающуюся на контур
.
скорость
изменения потока напряженности
электрического поля через поверхность,
опирающуюся на контур
.
|
Закон Био и Савара. |
|
Соображения Максвелла (Если магнитное поле вызывает электрическое, то почему бы не наоборот? Через 20 лет это было экспериментально доказано). До Максвелла этого никому не было известно. |
Частные случаи
Электромагнитные волны. |
|
“ (поле не меняется со временем): Когда поле постоянно, электрические и магнитные величины разделены и не зависят друг от друга. |
|
Пространственные производные скалярных и векторных полей
Общие и пространственные производные
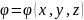
Definition: Общие и пространственные производные от скалярной или векторной функции называется предельное интегральное отношение.
Просnранственная производная от (чего-то) в данной точке поля:
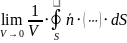
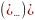 – скалярная или векторная
функция, соответствующая знаку умножения
(
– скалярная или векторная
функция, соответствующая знаку умножения
(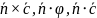
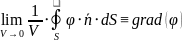
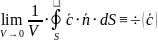
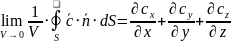
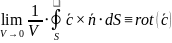
Ротор, дивергенция и градиент
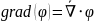
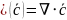
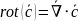
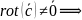 поле
вихревое (линии закручены)
поле
вихревое (линии закручены)
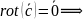 линии
поля прямые.
линии
поля прямые.
Смывание воды – можно наблюдать ротор поля скорости воды.
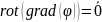
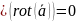
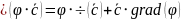
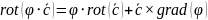
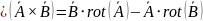
Теорема Гаусса
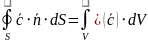
Поток вектора через замкнутую поверхность равен интегралу по объему, ограниченному данной поверхностью от дивергенции данного поля.
Теорема Стокса
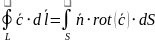
Циркуляция векторного поля по замкнутому полю равна потоку ротора этого поля через поверхность, опирающуюся на данный контур.
Послесловие
Скепсис – удел профессионалов.
Потенциальные и вихревые (соленоидальные) поля
Векторное поле в данной области пространства называется вихревым или соленоидальным, если в каждой точке этой области
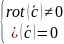 (есть вихрь, но нет потока)
(есть вихрь, но нет потока)Векторное поле в данной области пространства называется потенциальным, если в каждой точке этой области

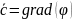
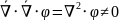
Векторное поле в данной области пространства называется гармоническим, если в каждой точке данной области
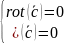
Уравнения Максвелла в дифференциальной форме
Рассмотрим пространство вакуума, в котором присутствуют электромагнитные поля, электрические заряды и токи.
Первое
Все
функции:
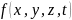
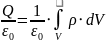
|
По теореме Гаусса |
|
Выполняется для любого объема V |
Значит,
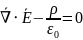
Первое
уравнение Максвелла в дифференциальной
форме
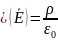
Третье
|
По теореме Гаусса |
|
Выполняется для любого объема V |
Значит,
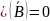
Третье уравнение Максвелла в дифференциальной форме
То есть, нету в природе магнитных зарядов.
Второе
Формула Лейбница для дифференцирования интегралов по параметру
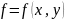
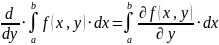
Выведение второго уравнения в дифференциальной форме из интегральной
Из формулы Лейбница получаем |
|
По теореме Стокса |
|
Таким образом, для любой поверхности S |
|
В силу произвольности поверхности S получаем |
|
Второе уравнение Максвелла в дифференциальной форме
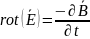
Четвертое
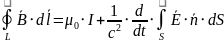
По теореме Стокса |
|
Сила тока по определению |
|
По формуле Лейбница |
|
В итоге получаем |
|
Поскольку поверхность выбирается произвольным образом, то получаем |
|
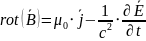

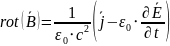

Четвертое уравнение максвелла в дифференциальной форме
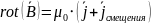
система уравнений Максвелла в дифференциальной форме
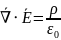
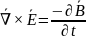
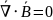
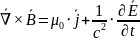
Слева – результат, справа – источник (причина)
Уравнения нужны для нахождения и
Система уравнений Максвелла-Лоренца
Частные случаи
“ ” |
Электростатика, поле потенциальное
Магнитостатика
|
Электромагнитные волны |
|
Закон сохранения электрического заряда

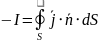
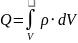
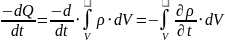
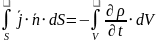
По теореме Гаусса |
|
Таким образом |
|
В силу произвольности выбора поверхности S |
|
Закон сохранения заряда в дифференциальной форме
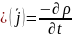
Убыль заряда вызывается его потоком из области
Проверка на соответствие уравнениям Максвелла
Четвертое уравнение Максвелла |
|
Умножаем скалярно обе части на оператор «набла» (берем дивергенцию слева и справа) |
|
|
|
|
|
Максвелл делал уравнения так, чтобы они удовлетворяли известным законам.
Энергия, импульс и момент импульса электромагнитного поля
Вектор плотности потока энергии электромагнитного поля (Вектор Пойнтинга)
Электромагнитное поле обладает ценными механическими свойствами.
Механика изучает движение тел в пространстве и времени.
Уравнения Максвелла, где есть , называют уравнениями движения:
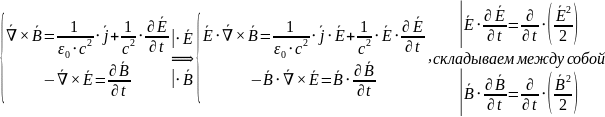
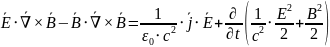
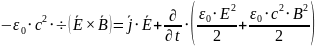
|
Энергия в единице объема |
|
Плотность энергии электрического поля |
|
Плотность энергии магнитного поля |
|
Плотность энергии электромагнитного поля |
Вектор Пойнтинга
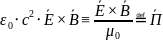
Вектор Пойнтинга – плотность потока энергии электромагнитного поля.
Закон сохранения энергии в электромагнитном поле
Дифференциальная форма
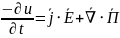
|
Работа, совершаемая над зарядом |
|
Поток энергии |
Убыль энергии происходит засчет работы над зарядом и потока энергии
Интегральная форма
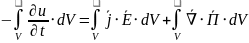
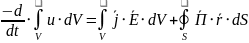
Плотность импульса электромгнитного поля (импульс единицы объема электромагнитного поля)
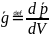
Теорема
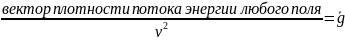
Где
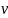 – скорость распространения энергии
поля.
– скорость распространения энергии
поля.
Для электромагнитного поля
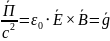
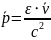
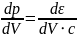
Нету такой инерциальной системы отсчета, где фотон покоится.
Плотность момента импульса электромагнитного поля (момент импульса в единице объема электромагнитного поля)
Механика:
|
Момент импульса |
|
Момент силы. Так как
|
Для
объема
 электромагнитного поля:
электромагнитного поля:
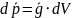
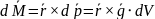
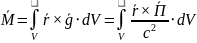
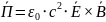
Электростатика и магнитостатика в вакууме
Уравнения Максвелла для электростатики
|
Первое уравнение Максвелла в интегральной форме – теорема Гаусса |
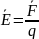
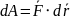
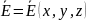
|
Работа на замкнутом пути равна нулю |
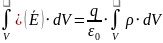
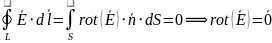
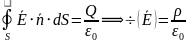
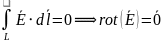
Уравнение Пуассона для электростатики
|
Поле безвихревое |
|
Работа электрического поля по замкнутому пути равна нулю |
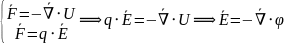
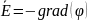
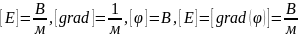
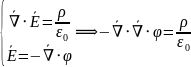
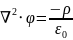
|
Лапласиан, оператор Лапласа |
|
Уравнение Пуассона |
|
Уравнение Лапласа |
Потенциал
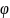 не имеет физического смысла, так как
его нельзя измерить.
не имеет физического смысла, так как
его нельзя измерить.
Поле непрерывно. Может иметь изломы, но не разрывы, так как иначе нельзя будет
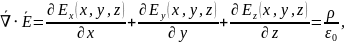
так
как в данном уравнении нужно брать
частные производные, для чего функция
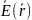 должна быть дифференцируемой, что, как
известно из курса математического
анализа, выполняется только в том случае,
когда функция непрерывна.
должна быть дифференцируемой, что, как
известно из курса математического
анализа, выполняется только в том случае,
когда функция непрерывна.
Потенциал также не может иметь разрыв.

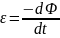
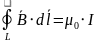
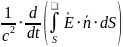
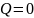 :
: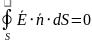
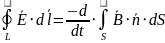
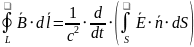
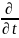 ”
”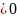
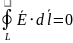
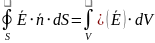
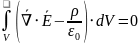
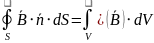
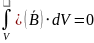
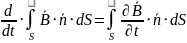
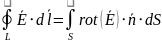
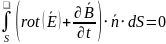
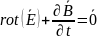
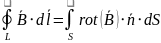
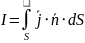
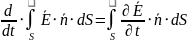
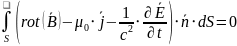
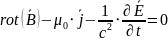
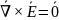
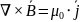
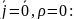
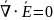
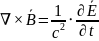
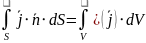
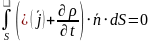
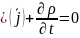
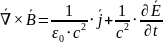
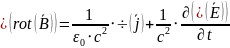
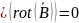
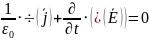
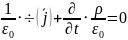

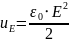

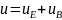
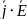
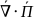
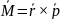
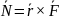
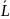 – функция Лагранжа
– функция Лагранжа