- •Лабораторная работа 6. Решение задач смешения с использованием тп ms excel
- •Решение
- •Какую максимальную прибыль можно получить за один день?
- •Сколько литров того и другого вина следует производить ежедневно?
- •Сколько процентов белого вина должно содержать вино «а»?
- •Сколько процентов розового вина должно содержать вино «в»?
- •На сколько гривень изменится прибыль винзавода, если поставки красного вина увеличатся до 1300 л в день, а поставки белого вина сократятся до 1800 л в день?
- •Задания для самостоятельной работы
- •Варианты 1-10
- •Варианты 11-20
- •Варианты 21-30
- •Какую максимальную прибыль можно получить за один день?
Лабораторная работа 6. Решение задач смешения с использованием тп ms excel
Тема: Оптимизационные микро- и макроэкономические модели: составление смесей
Цель: научиться решать задачи смешения с применением пакета «Поиск решений» в табличном процессоре MS EXCEL
Пример
Пусть на винзаводе производится две марки сухого вина: «А» и «В». Оптовые цены, по которым реализуются вина, составляют соответственно 7 и 6 гривень за литр. Ингредиентами для приготовления этих вин являются белое, розовое и красное сухие вина, закупаемые по ценам 7, 5 и 4 грн./л соответственно. В среднем на винзавод поставляется ежедневно 2000 л белого, 2500 л розового и 1200 л красного вина.
В вине «А» должно содержаться не менее 60 % белого и не более 20 % красного вина. Вино «В» должно содержать не более 60 % красного и не менее 15 % белого. Определите рецепты смешения ингредиентов для производства вин «А» и «В», обеспечивающие заводу максимальную прибыль.
Ответьте на поставленные вопросы:
Какую максимальную прибыль можно получить за один день?
Сколько литров того и другого вина следует производить ежедневно?
Сколько процентов белого вина должно содержать вино «А»?
Сколько процентов розового вина должно содержать вино «В»?
На сколько гривень изменится прибыль винзавода, если поставки красного вина увеличатся до 1300 л в день, а поставки белого вина сократятся до 1800 л в день?
Решение
Чтобы ответить на поставленные вопросы, необходимо:
а) построить математическую модель исходной задачи в общем виде;
б) решить полученную задачу линейного программирования симплексным методом или с применением ЭВМ (в частности, с использованием приложений MS Excel, POM for WINDOWS и других);
в) найти оптимальное решение двойственной задачи.
а) Данная задача относится к разделу «Многопродуктовые модели оптимального смешения», так как результатом смешения трех исходных вин (белого, красного и розового) должно получиться два сорта вина - «А» и «В», а критерием эффективности в ней является максимизация прибыли. При этом исходные ингредиенты и компоненты смеси совпадают (i = j).
Следуя принципам построения этой модели (модель С), получим ММ в общем виде. В этой модели xkj - количество j–ого ингредиента, входящего в k – ю смесь.
max Z = (7-7)x11 + (7-5)x12 + (7-4)x13 + (6-7)x21+ (6-5)x22+ (6-4)x23 |
|
x x21 ≥ 0,15 (x21 + x22 + x23 ) x13 ≤ 0,2 (x11 + x12 + x13 ) x23 ≤ 0,6 (x21 + x22 + x23 )
|
- ограничения на содержание компонентов в смеси;
|
x x12 + x22 ≤ 2500 x13 + x23 ≤ 1200
|
- ограничения на ежедневные запасы (объемы ингредиентов);
|
|
- условие неотрицательности переменных |
После раскрытия скобок и приведения подобных членов получим следующую ММ задачи в стандартной (симметричной) форме:
max Z = 2x12 + 3x13 – x21+ x22 + 2x23
-0,4x11 + 0,6 x12 + 0,6 x13 ≤ 0 -0,85 x21 + 0,15 x22 + 0,15 x23 ≤ 0 -0,2x11 - 0,2 x12 + 0,8 x13 ≤ 0 -0,6 x21 - 0,6 x22 + 0,4 x23 ≤ 0 x11 + x21 ≤ 2000 x12 + x22 ≤ 2500 x13 + x23 ≤ 1200
xkj ≥ 0, k = 1,2; j = 1,2,3. |
Двойственная задача выглядит следующим образом:
min F = 2000 у5 + 2500у6 + 1200 у7
- 0,6у1 -0,2 у3 + у6 ≥ 2 0,6у1 +0,8у3 + у7 ≥ 3 - 0,85у2 -0,6у4 + у5 ≥ -1 0,15у2 -0,6у4 + у6 ≥ 1 0,15у2 +0,4у4 + у7 ≥ 2
|
б) Для того, чтобы решить полученную задачу линейного программирования симплексным методом, необходимо записать ее в каноническом виде, т.е. ввести дополнительные переменные (пусть это будут gi, где i = 1,…7) в каждое неравенство и систему ограничений представить в виде системы линейных алгебраических уравнений.
max Z = 2x12 + 3x13 – x21+ x22 + 2x23
-0,4x11 + 0,6 x12 + 0,6 x13 + g1 = 0 -0,85 x21 + 0,15 x22 + 0,15 x23 + g2 = 0 -0,2x11 - 0,2 x12 + 0,8 x13 + g3 = 0 -0,6 x21 - 0,6 x22 + 0,4 x23 + g4 = 0 x11 + x21 + g5 = 2000 x12 + x22 + g6 = 2500 x13 + x23 + g7 = 1200
xkj ≥ 0, k = 1,2; j = 1,2,3; g i ≥ 0 , i = 1,…7. |
Можно решать задачу в симплекс-таблицах аналогично примеру, разобранному в задании №1. Однако, при большом числе переменных решение становится громоздким. Ниже предлагается описание процедуры решения оптимизационной задачи с применением приложения MS Excel.
Запустите приложение «MS Excel».
Составьте таблицу (табл. 2.2.1) входных данных на листе 1 с применением соответствующих формул.
Изменяемые ячейки – (D3 : I3), коэффициенты в целевой функции –
(D15 : I15). В ячейках С7 – С13 записываете формулы:
С7 =$D$3*D7+$E$3*E7+$F$3*F7+$G$3*G7+$H$3*H7+$I$3*I7 ….. С13 – =$D$3*D13+$E$3*E13+$F$3*F13+$G$3*G13+$H$3*H13+$I$3*I13 |
а в ячейках D16 – I16 записываете формулы:
D16 =D3*D15..…..I16 = I3*I15. |
=СУММ(D16:I16) |
Таблица 6.1
1 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
2 |
Кол-во ингредиентов |
|
|
x11 |
x12 |
x13 |
x21 |
x22 |
x23 |
3 |
в винах |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
6 |
Закупаемые ингредиенты |
Имеется |
Исполь- зовано |
|
|
|
|
|
|
7 |
|
0 |
0 |
-0,4 |
0,6 |
0,6 |
0 |
0 |
0 |
8 |
|
0 |
0 |
0 |
0 |
0 |
-0,85 |
0,15 |
0,15 |
9 |
|
0 |
0 |
-0,2 |
-0,2 |
0,8 |
0 |
0 |
0 |
10 |
|
0 |
0 |
0 |
0 |
0 |
-0,6 |
-0,6 |
0,4 |
11 |
Р1 |
2000 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
12 |
Р2 |
2500 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
13 |
Р3 |
1200 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
14 |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
0 |
2 |
3 |
-1 |
1 |
2 |
16 |
По видам закупаемого вина |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
17 |
|
|
|
|
|
|
|
|
|
18 |
ВСЕГО |
|
0 |
|
|
|
|
|
|
В «Меню» выберите вкладку «Сервис», затем «Поиск решения».
На открывшейся панели вводите следующие условия:
Установить целевую ячейку: $C$18.
Равной: (.) максимальному значению.
Изменяя ячейки: $D$3 : $I$3
Ограничения: $С$7 : $С$13 <=$B$7 : $B$13
$D$3 : $I$3 >= 0
Нажмите клавишу «Выполнить».
В течение заданного времени (обычно 100 с) появляется решение (табл.5.2).
Выбирая «Тип отчета», можно получить отчеты по результатам (табл.5.3), устойчивости (табл.5.4) и пределам (табл.5.5), из которых следует взять необходимые для ответов на поставленные вопросы данные.
Таблица 6.2
1 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
2 |
|
|
|
Кол-во нгредиентов в винах |
|||||
3 |
|
|
|
x11 |
x12 |
x13 |
x21 |
x22 |
x23 |
4 |
|
Имеется |
Использовано |
1526,6667 |
1017,7778 |
1,192 E-08 |
473,33333 |
1482,2222 |
1200 |
5 |
Закупаемые нгредиенты |
|
|
|
|
|
|
||
6 |
|
|
|
|
|
|
|||
7 |
|
0 |
4,228E-07 |
-0,4 |
0,6 |
0,6 |
0 |
0 |
0 |
8 |
|
0 |
-4,228E-07 |
0 |
0 |
0 |
-0,85 |
0,15 |
0,15 |
9 |
|
0 |
-508,88889 |
-0,2 |
-0,2 |
0,8 |
0 |
0 |
0 |
10 |
|
0 |
-693,33333 |
0 |
0 |
0 |
-0,6 |
-0,6 |
0,4 |
11 |
Р1 |
2000 |
2000 |
1 |
0 |
0 |
1 |
0 |
0 |
12 |
Р2 |
2500 |
2500 |
0 |
1 |
0 |
0 |
1 |
0 |
13 |
Р3 |
1200 |
1200 |
0 |
0 |
1 |
0 |
0 |
1 |
14 |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
0 |
2 |
3 |
-1 |
1 |
2 |
16 |
По видам закупаемого вина |
|
|
0 |
2035,55556 |
3,57628E-08 |
-473,33333 |
1482,22222 |
2400 |
17 |
|
|
|
|
|
|
|
|
|
18 |
ВСЕГО |
|
5444,4444 |
|
|
|
|
|
|
Таблица 6.3
Microsoft Excel 9.0 Отчет по результатам |
|
|
|||||||||||
Целевая ячейка (Максимум) |
|
|
|||||||||||
|
Ячейка |
Имя |
Исходно |
Результат |
|
|
|||||||
|
$C$18 |
ВСЕГО |
0 |
5444,444444 |
|
|
|||||||
Изменяемые ячейки |
|
|
|||||||||||
|
Ячейка |
Имя |
Исходно |
Результат |
|
|
|||||||
|
$D$3 |
x11 |
0 |
1526,666666 |
|
|
|||||||
|
$E$3 |
x12 |
0 |
1017,777778 |
|
|
|||||||
|
$F$3 |
x13 |
0 |
1,19209E-08 |
|
|
|||||||
|
$G$3 |
x21 |
0 |
473,3333338 |
|
|
|||||||
|
$H$3 |
x22 |
0 |
1482,222222 |
|
|
|||||||
|
$I$3 |
x23 |
0 |
1200 |
|
|
|||||||
|
|
Ограничения |
|||||||||||
|
|
|
Ячейка |
Имя |
Значение |
формула |
Статус |
Разница |
|||||
|
|
|
$C$7 |
|
4,22837E-07 |
$C$7<=$B$7 |
связанное |
0 |
|||||
|
|
|
$C$8 |
|
-4,22836E-07 |
$C$8<=$B$8 |
связанное |
0 |
|||||
|
|
|
$C$9 |
|
-508,8888889 |
$C$9<=$B$9 |
не связан. |
508,8888889 |
|||||
|
|
|
$C$10 |
|
-693,3333333 |
$C$10<=$B$10 |
не связан. |
693,3333333 |
|||||
|
|
|
$C$11 |
Р1 |
2000 |
$C$11<=$B$11 |
связанное |
0 |
|||||
|
|
|
$C$12 |
Р2 |
2500 |
$C$12<=$B$12 |
связанное |
0 |
|||||
|
|
|
$C$13 |
Р3 |
1200 |
$C$13<=$B$13 |
связанное |
0 |
|||||
|
|
|
$D$3 |
x11 |
1526,666666 |
$D$3>=0 |
не связан. |
1526,666666 |
|||||
|
|
|
$E$3 |
x12 |
1017,777778 |
$E$3>=0 |
не связан. |
1017,777778 |
|||||
|
|
|
$F$3 |
x13 |
1,19209E-08 |
$F$3>=0 |
связанное |
0 |
|||||
|
|
|
$G$3 |
x21 |
473,3333338 |
$G$3>=0 |
не связан. |
473,3333338 |
|||||
|
|
|
$H$3 |
x22 |
1482,222222 |
$H$3>=0 |
не связан. |
1482,222222 |
|||||
|
|
|
$I$3 |
x23 |
1200 |
$I$3>=0 |
не связан. |
1200 |
|||||
Таблица 6.4
Microsoft Excel 9.0 Отчет по устойчивости |
||||||||
|
||||||||
Изменяемые ячейки |
Ограничения |
|||||||
|
|
Результ. |
Нормир. |
|
|
Результ. |
Лагранжа |
|
Ячейка |
Имя |
значение |
градиент |
Ячейка |
Имя |
значение |
Множитель |
|
$D$3 |
x11 |
1526,666666 |
0 |
$C$7 |
|
4,22837E-07 |
2,222222134 |
|
$E$3 |
x12 |
1017,777778 |
0 |
$C$8 |
|
-4,22836E-07 |
2,222222134 |
|
$F$3 |
x13 |
1,19209E-08 |
-2,04643E-06 |
$C$9 |
|
-508,8888889 |
0 |
|
$G$3 |
x21 |
473,3333338 |
0 |
$C$10 |
|
-693,3333333 |
0 |
|
$H$3 |
x22 |
1482,222222 |
0 |
$C$11 |
Р1 |
2000 |
0,888888867 |
|
$I$3 |
x23 |
1200 |
0 |
$C$12 |
Р2 |
2500 |
0,666666667 |
|
|
|
|
|
$C$13 |
Р3 |
1200 |
1,666666667 |
|
Таблица 6.5
Microsoft Excel 9.0 Отчет по пределам |
||||||||
Целевое |
||||||||
Ячейка |
Имя |
значение |
||||||
$C$18 |
ВСЕГО |
5444,444444 |
||||||
|
Изменяемое |
|
|
Нижний |
Целевое |
Верхний |
Целевое |
|
Ячейка |
Имя |
значение |
|
предел |
результат |
предел |
результат |
|
$D$3 |
x11 |
1526,666666 |
|
1526,666666 |
5444,444444 |
1526,666666 |
5444,444444 |
|
$E$3 |
x12 |
1017,777778 |
|
0 |
3408,888888 |
1017,777777 |
5444,444443 |
|
$F$3 |
x13 |
1,19209E-08 |
|
1,19209E-08 |
5444,444444 |
1,19209E-08 |
5444,444444 |
|
$G$3 |
x21 |
473,3333338 |
|
473,3333338 |
5444,444444 |
473,3333338 |
5444,444444 |
|
$H$3 |
x22 |
1482,222222 |
|
326,6666662 |
4288,888889 |
1482,222222 |
5444,444444 |
|
$I$3 |
x23 |
1200 |
|
0 |
3044,444444 |
1200 |
5444,444444 |
|
Ответы на поставленные вопросы:

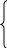 11
≥ 0,6 (x11
+ x12
+ x13
)
11
≥ 0,6 (x11
+ x12
+ x13
)
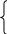 11
+ x21
≤ 2000
11
+ x21
≤ 2000
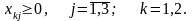
 0,4у1
- 0,2у3 + у5
≥ 0
0,4у1
- 0,2у3 + у5
≥ 0