19. Закон Гука при растяжении и сжатии.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

Рисунок 1.12.1. Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: 

Fx = Fупр = –kx.

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –F_упр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ: 

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например,E ≈ 2·10¹¹ Н/м², а для резины E ≈ 2·10⁶ Н/м², т. е. на пять порядков меньше.

20. Расчетная схема при растяжении и сжатии. Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только нормальная сила.Рассмотрим расчетную схему бруса постоянного поперечного сечения с заданной внешней сосредоточенной нагрузкой Р и распределенной q, (рис.1).

а) расчетная схема, б) первый участок, левая отсеченная часть, в) второй участок, левая отсеченная часть, г) второй участок, правая отсеченная часть, д) эпюра нормальных сил

Рис.1. Построение эпюры нормальных сил: 

Пусть  . Прежде всего определим опорную реакцию R, задавшись ее направлением вдоль оси х.

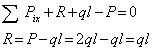
Брус имеет 2 участка 1 и 2.

В пределах первого участка мысленно рассечем брус на 2 части нормальным сечением и рассмотрим равновесие, допустим левой части, введя следующую координату х₁, рис.1 б:

Следовательно, в пределах первого участка брус претерпевает сжатие постоянной нормальной силой.Аналогично поступим со вторым участком. Мысленно рассечем его сечением 2—2, и рассмотрим равновесие левой части (рис.1 в).Установим предварительно границы изменения х₂:

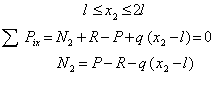
Подставляя граничные значения параметра х₂, получим:

Таким образом, в пределах второго участка брус растянут и нормальная сила изменяется по линейному закону.

Аналогичный результат получается и при рассмотрении правой отсеченной части (рис.1 г):

На основе полученных данных строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (рис.1 д). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил R и Р, что в свою очередь может служить правилом правильности выполненных построений.