
- •15 Динамика механика
- •Глава 1. Кинематика
- •1.1. Закон движения материальной точки
- •1.2. Скорость определяет быстроту движения.
- •Чтобы определить скорость изменения функции, надо взять производную этой функции по времени.
- •1.3. Ускорение
- •1.4. Кинематика вращательного движения
- •Глава 2. Динамика
- •2.1.Первый закон Ньютона (закон инерции)
- •2.2. Второй закон Ньютона
- •Изменение импульса (количества движения) за время равно импульсу силы за это же время.
- •2.3. Третий закон Ньютона
- •2.4. Сохраняющиеся величины
- •2.5. Основной закон динамики для системы материальных точек. Закон сохранения импульса.
- •Скорость изменения импульса системы материальных точек равна векторной сумме внешних сил.
- •2.6. Центр инерции
- •Глава 3. Работа и энергия
- •3.1.Работа силы и ее выражение через криволинейный интеграл
- •3.2.Мощность
- •3.3. Кинетическая энергия
- •3.4. Потенциальная энергия
- •3.5. Потенциальные кривые
- •3.6.Закон сохранения механической энергии
- •3.7. Соударения
- •Глава 4. Механика вращательного движения
- •4.1. Кинетическая энергия вращательного движения. Момент инерции.
- •4.3. Второй закон Ньютона вращательного движения.
- •4.4. Момент импульса. Закон сохранения момента импульса.
- •4.5. Таблица соответствия поступательного и вращательного движений
- •Работа и энергия
- •Глава 5 механические колебания и волны
- •5.1.Основные понятия
- •5.2.Дифференциальное уравнение свободных гармонических колебаний
- •5.3. Примеры свободных гармонических колебаний
- •5.4. Затухающие колебания.
- •5.5. Вынужденные колебания
- •5.6. Автоколебания.
- •5.7.Сложение колебаний.
- •Глава 6. Механические (упругие ) волны. Звук
- •6.1. Характеристики упругих волн
- •6.2. Уравнение бегущей волны
- •Основы молекулярной физики и термодинамики
- •Глава 7. Основы молекулярно–кинетической теории
- •7.1. Основные понятия и определения
- •7.2. Уравнение состояния идеального газа
- •7.3. Основное уравнение молекулярно–кинетической теории идеального газа (основное уравнение мкт)
- •Абсолютная температура является мерой средней кинетической энергии поступательного движения молекулы.
- •7.4. Закон распределения молекул по скоростям
- •7.5. Барометрическая формула #
- •Глава 8 основы термодинамики
- •8.1. Первый закон термодинамики
- •6.2. Простейшие процессы в идеальных газах
- •8.3. Второй закон термодинамики
- •8.4. Цикл Карно
- •Глава 9 реальные газы
- •9.1. Уравнение состояния реальных газов (уравнение Ван–дер–Ваальса).
- •9.2.Изотермы реальных газов
5.4. Затухающие колебания.
Затухающими колебаниями называются колебания, механическая энергия которых расходуется на работу против диссипативных сил (силы трения).
![]()
Амплитуда и частота колебаний уменьшаются, колебания затухают.
Дифференциальное уравнение затухающих колебаний.
Для случая малых колебаний в отсутствии сухого трения можно считать, что сила трения равна
![]() ,
— коэффициент трения.
,
— коэффициент трения.
Для малых колебаний
основной закон динамики будет иметь
вид:
![]()
![]() ,
,
где
![]() —
коэффициент затухания,
—
коэффициент затухания,
![]() — собственная частота свободных
колебаний.
— собственная частота свободных
колебаний.
Рис.
4.4.1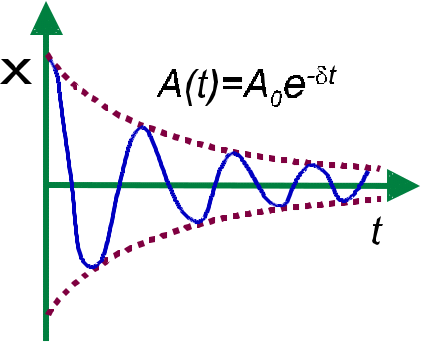 Рис.5.4.1
Рис.5.4.1
выбирается
в виде гармонической функции
![]() амплитуда которой
экспоненциально убывает со временем
(рис 5.4.1):
амплитуда которой
экспоненциально убывает со временем
(рис 5.4.1):
![]() .
.
Циклическая
частота затухающих колебаний определяется
формулой
![]() .
.
Логарифмическим
декрементом затухания
![]() называется натуральный логарифм
отношения амплитуд соседних колебаний
в моменты времени:
называется натуральный логарифм
отношения амплитуд соседних колебаний
в моменты времени:
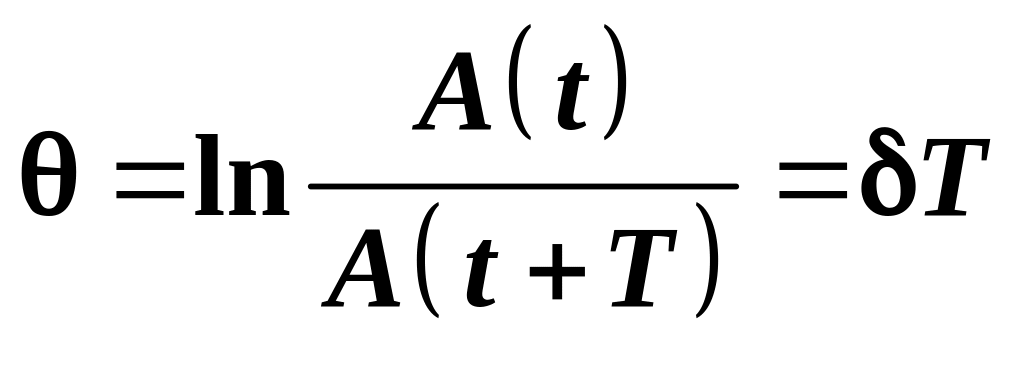 .
.
Время релаксации:
![]() — время за которое амплитуда колебаний
уменьшается в
— время за которое амплитуда колебаний
уменьшается в
![]() раз.
раз.
![]() — количество
колебаний после которых амплитуда
колебаний уменьшается в
— количество
колебаний после которых амплитуда
колебаний уменьшается в
![]() раз.
раз.
5.5. Вынужденные колебания
Вынужденные гармонические колебания происходят под действием трех сил: квазиупругой, сопротивления и внешней вынуждающей силы, которая меняется по гармоническому закону:
![]() ,
где
,
где
![]() – циклическая
частота вынуждающей силы,
– циклическая
частота вынуждающей силы,
![]() – максимальное
значение (амплитуда) силы.
– максимальное
значение (амплитуда) силы.
Установившиеся вынужденные колебания являются гармоническими и совершаются с частотой вынуждающей силы .
Дифференциальное уравнение вынужденных колебаний.
Для малых колебаний основной закон динамики будет иметь вид:
![]()
![]() ,
,
где
![]() — коэффициент затухания (5.4.),
— коэффициент затухания (5.4.),
![]() — собственная
частота свободных колебаний.
— собственная
частота свободных колебаний.
Решение дифференциального уравнения вынужденных колебаний выбирается в виде гармонической функции:
![]() ,
,
где
![]() — сдвиг фазы между смещением
— сдвиг фазы между смещением
![]() и вынуждающей силой
и вынуждающей силой
![]() .
.
![]() — амплитуда
колебаний зависит от соотношения
— амплитуда
колебаний зависит от соотношения
![]() и
.
и
.
Резонансные
кривые
 Рис.
5.5.1
Рис.
5.5.1
На рисунке 5.5.1
приведены кривые зависимости амплитуды
А
от циклической частоты вынуждающей
силы
![]() — резонансные кривые.
— резонансные кривые.
При
 амплитуда
амплитуда
 — статическая деформация системы под
действием постоянной внешней силы
.
— статическая деформация системы под
действием постоянной внешней силы
.При
 ,
,
 .
.При
 наступает резонанс
— явление резкого возрастания амплитуды
вынужденных колебаний при приближении
циклической частоты вынуждающей силы
к собственной частоте системы
(рис.5.5.1). Амплитуда увеличивается до
тех пор, пока работа сил трения не
сравняется с работой внешней силы. При
отсутствии трения
наступает резонанс
— явление резкого возрастания амплитуды
вынужденных колебаний при приближении
циклической частоты вынуждающей силы
к собственной частоте системы
(рис.5.5.1). Амплитуда увеличивается до
тех пор, пока работа сил трения не
сравняется с работой внешней силы. При
отсутствии трения
 возрастание амплитуды неограниченно.
возрастание амплитуды неограниченно.
5.6. Автоколебания.
 Рис.
5.6.1
Рис.
5.6.1 Рис.
5.6.2
Рис.
5.6.2
На рис.5.6.2. показана автоколебательная система с отрицательной обратной связью (сифон). Негармонические колебания совершает уровень воды в сосуде.
Рис.
5.6.3
а) Колебательная система.
б) Источник энергии, компенсирующий потери энергии.
в) Клапан – устройство, регулирующее поступление энергии в колебательную систему.
г) Обратная связь – основной признак автоколебательной системы – устройство для обратного воздействия автоколебательной системы на клапан.
Положительная обратная связь "раскачивает", возбуждает систему, отрицательная – возвращает систему в исходное положение.
