
- •Тема 1. Диференціальні рівняння.
- •2. Розв’язати задачу Коші значить:
- •8. Розв’язок диференціального рівняння називають особливим розв’язком, якщо:
- •9. Для того, щоб рівняння було б рівнянням в повних диференціалах, необхідно і достатньо виконання умови
- •11. Диференціальне рівняння , де - дійсні числа, називається:
- •22. Загальний розв’язок лінійного неоднорідного диференціального рівняння має вигляд:
- •24. Якщо права частина лінійного неоднорідного диференціального рівняння дорівнює , а і - розв’язки рівнянь та , то розв’язком даного рівняння є:
- •Тема 2. Ряди.
- •25. Вираз , де - послідовність дійсних або комплексних чисел, називають:
- •34. Вирази , де - послідовність дійсних або комплексних чисел, називають:
- •43. Число, яке визначається формулою , називають:
- •51. Для наближених обчислень використовують розклад функції в::
- •Тема 3. Диференціальне та Інтегральне числення функції багатьох змінних.
- •61. Знайти межі інтегрування для ,
- •63. Функція f(X) називається первісною для функції f(X) на проміжку (a;b), якщо виконується рівність:
- •64. Змінити порядок інтегрування в подвійному інтегралі
- •74. Знайти межі інтегрування для ,
- •86. Змінити порядок інтегрування в подвійному інтегралі
- •88. Подвійний інтеграл від функції по області, що обмежена прямими
- •89. Змінити порядок інтегрування в подвійному інтегралі
- •2. Завдання 2 рівня.
- •Тема 1. Диференціальні рівняння.
- •Тема 2. Ряди.
- •95. Знайти відповідність між сумою перших трьох членів ряду та його загальним виглядом:
- •Тема 3. Диференціальне та Інтегральне числення функції багатьох змінних.
- •99. Встановіть відповідність між функціями та їх похідними.
- •3. Завдання 3 рівня.
- •Тема 1. Диференціальні рівняння.
- •Тема 2. Ряди.
- •Тема 3. Диференціальне та Інтегральне числення функції багатьох змінних.
22. Загальний розв’язок лінійного неоднорідного диференціального рівняння має вигляд:
-
А
Б
В
Г
Д
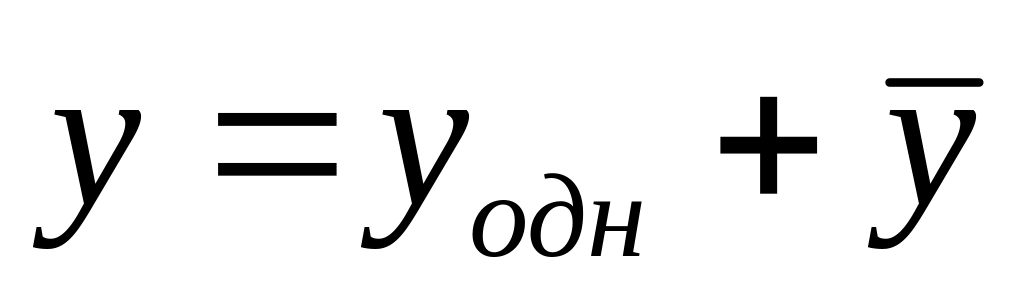 ,
де
,
де
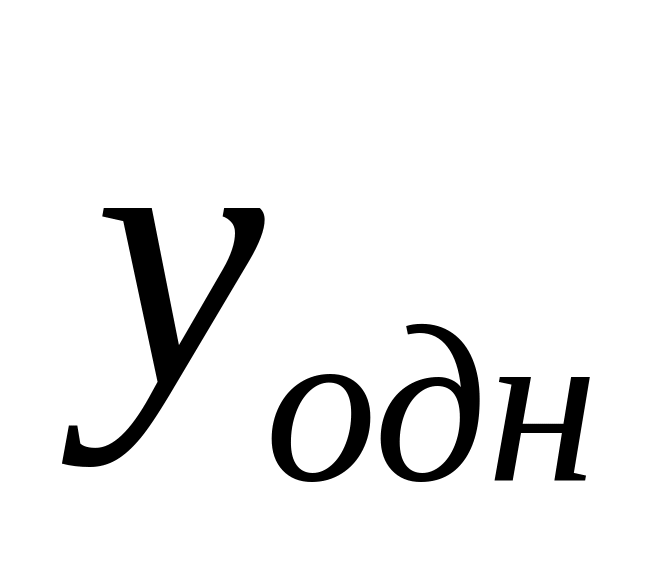 -
загальний розв’язок
відповідного однорідного лінійного
рівняння,
-
загальний розв’язок
відповідного однорідного лінійного
рівняння,
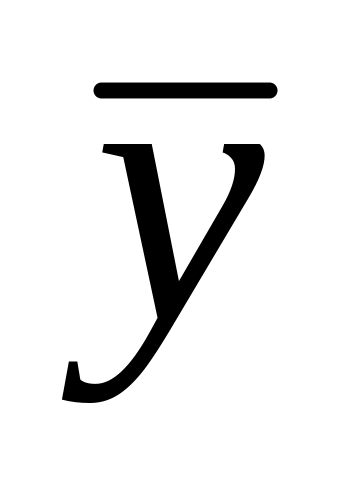 -
частинний розв’язок
заданого рівняння
-
частинний розв’язок
заданого рівняння, де - частинний розв’язок відповідного однорідного лінійного рівняння, - загальний розв’язок заданого рівняння
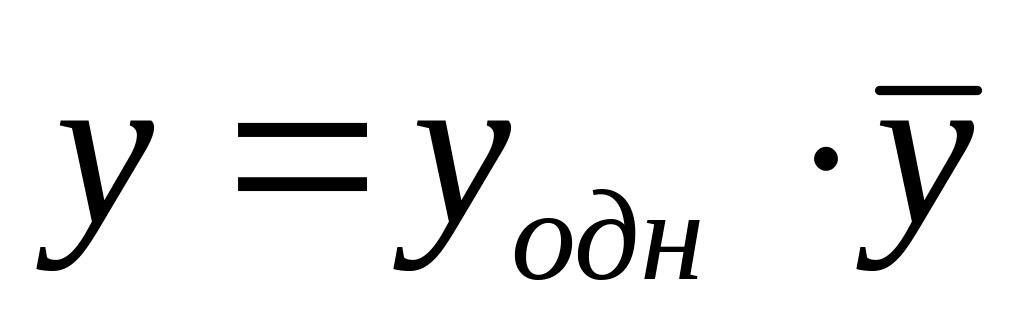 ,
де
-
загальний розв’язок
відповідного однорідного лінійного
рівняння,
-
частинний розв’язок
заданого рівняння
,
де
-
загальний розв’язок
відповідного однорідного лінійного
рівняння,
-
частинний розв’язок
заданого рівняння, де - довільний розв’язок відповідного однорідного лінійного рівняння, - довільний розв’язок заданого рівняння
, де - довільний розв’язок відповідного однорідного лінійного рівняння, - довільний розв’язок заданого рівняння
23.
Якщо права частина лінійного неоднорідного
диференціального рівняння дорівнює
![]() ,
де
і
,
де
і![]() -
многочлени степенів n
і s
відповідно, то фіксований розв’язок
цього рівняння шукають у вигляді:
-
многочлени степенів n
і s
відповідно, то фіксований розв’язок
цього рівняння шукають у вигляді:
-
А
Б
В
Г
Д
, де - многочлен степеня п з невизначеними коефіцієнтами, r – кратність кореня α відповідного характеристичного рівняння
де - многочлени степеня з невизначеними коефіцієнтами, r – кратність кореня відповідного характеристичного рівняння
де a і b – невідомі коефіцієнти , r – кратність кореня відповідного характеристичного рівняння
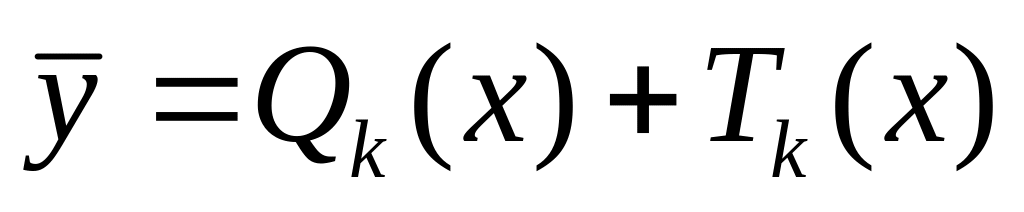 де
-
многочлени степеня
з
невизначеними коефіцієнтами
де
-
многочлени степеня
з
невизначеними коефіцієнтамиде - многочлени степеня з невизначеними коефіцієнтами
24. Якщо права частина лінійного неоднорідного диференціального рівняння дорівнює , а і - розв’язки рівнянь та , то розв’язком даного рівняння є:
-
А
Б
В
Г
Д
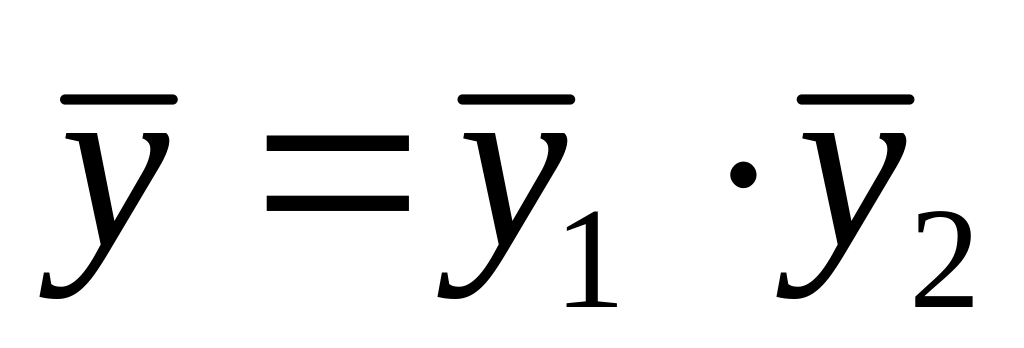
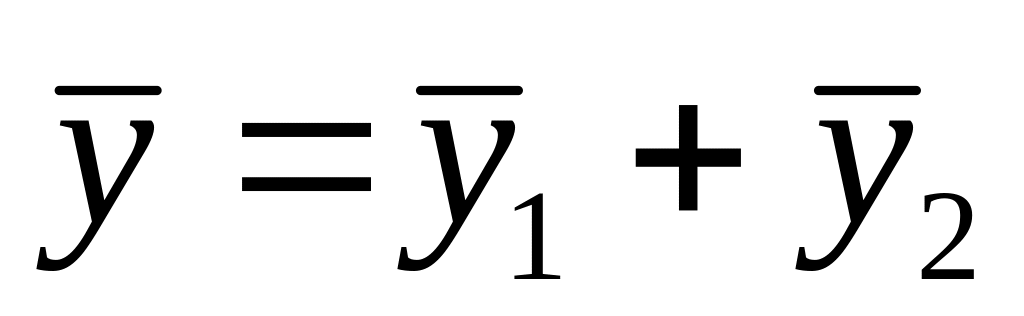
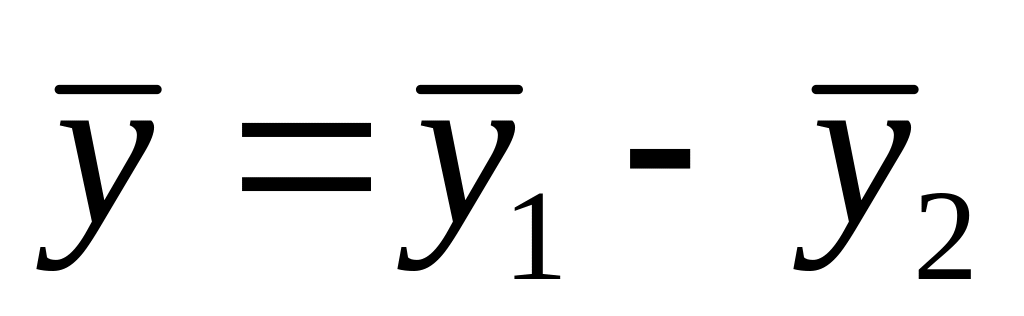
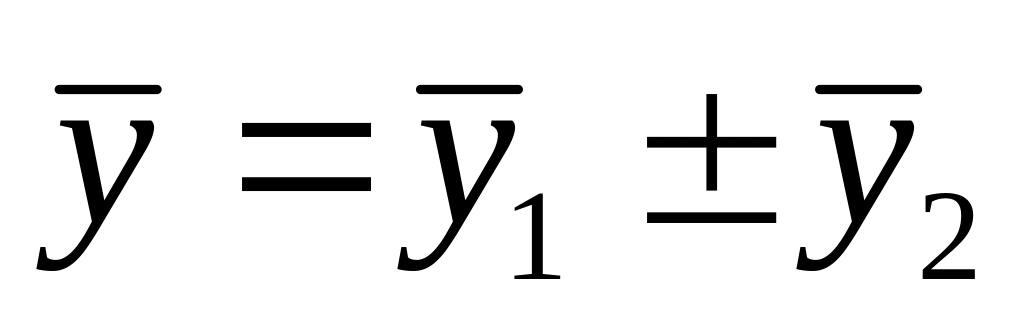
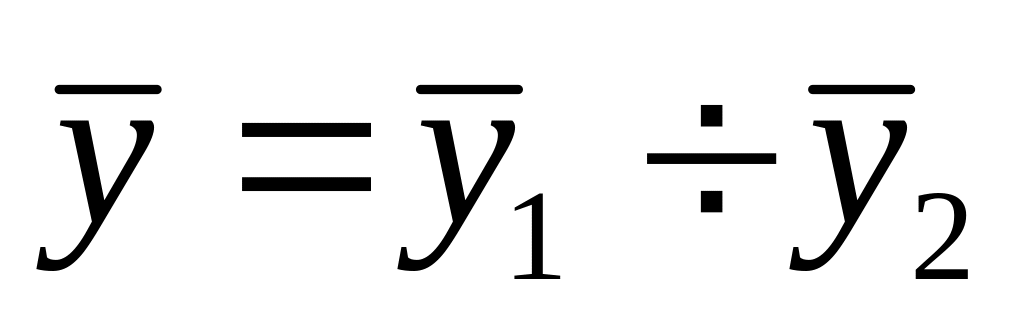
Тема 2. Ряди.
25. Вираз , де - послідовність дійсних або комплексних чисел, називають:
-
А
Б
В
Г
Д
сумою чисел
послідовністю
числовим змістом
частинними сумами
числовим рядом
26. Якщо
послідовність
![]() ряду
збіжна, тобто
ряду
збіжна, тобто
![]() ,
то ряд називається:
,
то ряд називається:
-
А
Б
В
Г
Д
збіжним
числовим
розбіжним
знакозмінним
степеневим
27. Якщо
загальний член ряду
![]() не
прямує до нуля при
не
прямує до нуля при
![]() ,
то ряд називається:
,
то ряд називається:
-
А
Б
В
Г
Д
збіжним
числовим
розбіжним
знакозмінним
степеневим
28. Якщо
задано два ряди з невід’ємними членами
![]() та
та
![]() і
для всіх п
виконується нерівність
і
для всіх п
виконується нерівність
![]() ,
тоді:
,
тоді:
-
А
Б
В
Г
Д
ряди рівні
якщо ряд розбіжний, то і ряд також розбіжний
якщо ряд збіжний, то ряд розбіжний
якщо ряд збіжний, то і ряд також збіжний
якщо ряд розбіжний, то ряд збіжний
29.
Якщо для ряду
існує
границя
![]() ,
тоді:
,
тоді:
-
А
Б
В
Г
Д
при 0≤d<1 ряд розбіжний, при d>1 ряд збіжний, при d=1 ряд може бути як збіжним так і розбіжним
при 0≤d<1 ряд збіжний, при d>1 ряд розбіжний, при d=1 ряд може бути як збіжним так і розбіжним
ряд збіжний
при d<1 ряд збіжний, при d≥1 ряд розбіжний
знакододатній
30. Якщо
для ряду
![]() виконуються
умови:
виконуються
умови:
![]() >
>![]() >…>
>…>![]() >…для
кожного
>…для
кожного
![]() ,
,
![]() ,
тоді він:
,
тоді він:
-
А
Б
В
Г
Д
збіжний
розбіжний
степеневий
функціональний
знакододатний
31. Ряд
![]() ,
де
,
де
![]() - функції, визначені на деякій множині
Е,
називається:
- функції, визначені на деякій множині
Е,
називається:
-
А
Б
В
Г
Д
числовим
знакозмінним
степеневим
функціональним
знакододатним
32. Якщо
степеневий ряд
![]() збіжний
при х=х0,
то для всіх значень х,
що задовольняють нерівність
збіжний
при х=х0,
то для всіх значень х,
що задовольняють нерівність
![]() <
<![]() ,
він буде:
,
він буде:
-
А
Б
В
Г
Д
числовим
знакозмінним
розбіжним
умовно збіжним
абсолютно збіжним
33. Вираз
![]() називається:
називається:
-
А
Б
В
Г
Д
набором функцій
множиною похідних функцій
рядом Тейлора
рядом Маклорена
функцією від похідних
