12. Системный анализ

Системный анализ — научный метод познания, представляющий собой последовательность действий по установлению структурных связей между переменными или элементами исследуемой системы. Опирается на комплекс общенаучных, экспериментальных, естественнонаучных, статистических, математических методов.

Истоки системного анализа

Системный анализ возник в эпоху разработки компьютерной техники. Успех его применения при решении сложных задач во многом определяется современными возможностями информационных технологий. Н.Н. Моисеев приводит, по его выражению, довольно узкое определение системного анализа [1]: «Системный анализ — это совокупность методов, основанных на использовании ЭВМ и ориентированных на исследование сложных систем — технических, экономических, экологических и т.д. Результатом системных исследований является, как правило, выбор вполне определенной альтернативы: плана развития региона, параметров конструкции и т.д. Поэтому истоки системного анализа, его методические концепции лежат в тех дисциплинах, которые занимаются проблемами принятия решений: теории операций и общей теории управления».

Существо системного анализа

Ценность системного подхода состоит в том, что рассмотрение категорий системного анализа создает основу для логического и последовательного подхода к проблеме принятия решений. Эффективность решения проблем с помощью системного анализа определяется структурой решаемых проблем.

Классификация проблем

Согласно классификации, все проблемы подразделяются на три класса:

хорошо структурированные (well-structured), или количественно сформулированные проблемы, в которых существенные зависимости выяснены очень хорошо;

неструктурированные (unstructured), или качественно выраженные проблемы, содержащие лишь описание важнейших ресурсов, признаков и характеристик, количественные зависимости между которыми совершенно неизвестны;

слабо структурированные (ill-structured), или смешанные проблемы, которые содержат как качественные элементы, так и малоизвестные, неопределенные стороны, которые имеют тенденцию доминировать.

Методы решения

Для решения хорошо структурированных количественно выражаемых проблем используется известная методология исследования операций, которая состоит в построении адекватной математической модели (например, задачи линейного, нелинейного, динамического программирования, задачи теории массового обслуживания, теории игр и др.) и применении методов для отыскания оптимальной стратегии управления целенаправленными действиями.

Процедура принятия решений

Для решения слабо структурированных проблем используется методология системного анализа, системы поддержки принятия решений (СППР). Рассмотрим технологию применения системного анализа к решению сложных задач.

Процедура принятия решений согласно [2] включает следующие основные этапы:

формулировка проблемной ситуации;

• определение целей;

• определение критериев достижения целей;

• построение моделей для обоснования решений;

• поиск оптимального (допустимого) варианта решения;

• согласование решения;

• подготовка решения к реализации;

• утверждение решения;

• управление ходом реализации решения;

• проверка эффективности решения.

Для многофакторного анализа, алгоритм можно описать и точнее:

• описание условий (факторов) существования проблем, И, ИЛИ и НЕ связывание между условиями;

• отрицание условий, нахождение любых технически возможных путей. Для решения нужен хотя бы один единственный путь. Все И меняются на ИЛИ, ИЛИ меняются на И, а НЕ меняются на подтверждение, подтверждение меняется на НЕ-связывание;

• рекурсивный анализ вытекающих проблем из найденных путей, т.е. п.1 и п.2 заново для каждой подпроблемы;

• оценка всех найденных путей решений по критериям исходящих подпроблем, сведенным к материальной или иной общей стоимости.

14.Основные определения матричных игр. Оптимальные чистые стратегии

Принципиально иная ситуация возникает при изучении процессов принятия решений несколькими субъектами, ин­тересы которых могут не совпадать. При этом возникают за­дачи со многими целевыми функциями (критериями). Об­ласть математики, изучающая данные проблемы, получила название теории игр. Задачи теории игр относятся к области принятия решений в условиях неопределенности, а их специ­фика состоит в том, что, как правило, подразумевается нео­пределенность, возникающая в результате действий двух или более «разумных» противников, способных оптимизировать свое поведение за счет других. Среди типичных примеров та­кого поведения могут быть названы действия конкурирующих фирм на одном рынке или планирование военных операций.

Особенностью теории игр как научной дисциплины стала употребляемая в ней специфическая терминология. Термин «игра» применяется для обозначения совокупности правил и соглашений, которыми руководствуются субъекты, поведе­ние которых мы изучаем. Каждый такой субъект k, где , или игрок характеризуется наличием индивидуаль­ной системы целевых установок и стратегий , т. е. возможных вариантов действии в игре.

Достаточно распространенный способ математического опи­сания игры основан на задании функций каждая из которых определяет результат (платеж, выигрыш), получаемый k-м игроком в зависимости от набора стратегий , примененного всеми участниками игры. Функции также называют функциями выигрыша или платежными функциями. В том случае, если для любых S , то игра называется игрой с нулевой суммой.

Игру с двумя участниками и нулевой суммой называют антагонистической. Антагонистические игры, т. е. игры, в ко­торых выигрыш одного участника равен проигрышу другого, в силу относительно простой постановки задачи являются наиболее изученным разделом теории игр. Однако содержа­ние теории игр, безусловно, не исчерпывается ими. В класси­фикации игровых моделей выделяют игры с конечными и бесконечными наборами стратегий у игроков, выделяют игры по возможным количествам ходов у участников. Также игры делят на некооперативные и кооперативные, т. е. те, в кото­рых функции выигрыша участников зависят от образуемых ими коалиций. Помимо этого игры можно различать по объе­му информации, имеющейся у игроков относительно про­шлых ходов. В этой связи они делятся на игры с полной и не­полной информацией.

Рассмотрим более подробно антагонистические игры, и их основные свойства. Удобным способом задания игры двух участников с нулевой суммой является платежная матрица. Каждый элемент платежной матрицы ai,j содержит числовое значение выигрыша игрока I (проигрыша игрока II), если первый применяет стратегию i, а второй — стратегию j. Термины выигрыш и проигрыш следует понимать в широком смысле, так как они могут принимать отрицательные значе­ния и с житейской точки зрения означать противоположное. Нетривиальность задачи, прежде всего заключается в том, что каждый из игроков делает свой выбор, не зная о выборе дру­гого, что существенно осложняет процесс оптимизации вы­бираемой стратегии.

К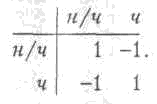 лассическим примером антагонистической игры являет­ся игра с двумя участниками, загадывающими независимо друг от друга числа. Предполагается, что если их сумма ока­зывается четной, то выигрыш, равный 1, достается первому игроку, а если нечетной, то второму. Если для обоих игроков загадывание нечетного числа является первой стра­тегией, а четного — второй, можем записать платежную матрицу данной игры:

Строки матрицы соответствуют стратегиям игрока I, столбцы — стратегиям игрока II, а ее элементы — результа­там первого игрока. Также из определения игры следует, что элементы данной матрицы, взятые с обратным знаком, соот­ветствуют выигрышам второго игрока.

Более сложная и содержательная платежная матрица мо­жет быть получена, если несколько модифицировать предло­женную игру. Допустим, что оба участника имеют право зага­дывать числа от 1 до 4, что составляет их соответствующие стратегии. В случае, если результат сложения задуманных чисел будет четным, то второй игрок выплачивает первому получившуюся сумму, а, если нечетным, то первый — второ­му. Запишем платежную матрицу для такой игры:

К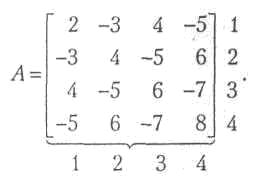 ак уже отмечалось, важнейшим в теории игр является вопрос об оптимальности решения (выбора стратегии) для каждого из игроков. Проанализируем с этой точки зрения не­которую матричную игру, для которой задана платежная матрица

При выборе игроком I стратегии i, его гарантированный доход независимо от действий игрока II составит minj(аi,j) По­скольку он может выбирать i самостоятельно, то целесооб­разно этот выбор сделать таким, чтобы он при любой страте­гии противника максимизировал величину гарантированно­го дохода, т. е. обеспечивал получение maxi(minj(ai,j))

Такой принцип выбора стратегии получил название «принцип максимина». С другой стороны, аналогичные рассуждения могут быть проведены по поводу, действий второго игро­ка. Его наибольший проигрыш при выборе стратегии j соста­вит maxi(ai,j) и, следовательно, ему следует выбирать стратегию так, чтобы минимизировать величину проигрыша при любых действиях соперника, т. е. обеспечить minj(maxi(ai,j)) В этом суть принципа минимакса.

Можно доказать справедливость следующего соотношения: maxi(minj(ai,j)) minj(maxi(ai,j))

Однако очевидный интерес представляет ситуация, при которой значение выигрыша (платежа), получаемого игро­ком I при выборе им максиминной стратегии, равно платежу (проигрышу) II игрока при минимаксной стратегии maxi(minj(ai,j))=minj(maxi(ai,j))

В этом случае говорят, что игра имеет седловую точку. Совпадение значений гарантированных выигрышей игроков при максиминной и минимальной стратегии означает воз­можность достижения в игре некоторого оптимального состояния, от которого не выгодно отклоняться ни одному из участников. Понятие «оптималь­ность» здесь означает, что ни один разумный (осторожный) игрок не стремится изменить свою стратегию, так как его про­тивник, в принципе, сможет выбрать такую стратегию, которая даст худший для первого результат. Стратегии i* и j*— стра­тегии, образующие седловую точку, называются оптимальны­ми, а значение =ai*,j* называют ценой игры. Тройка (i*,j*, ) считается решением матричной игры с седловой точкой.

Н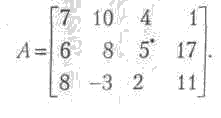 етрудно заметить, что не всякая игра обладает седловой точкой. Примером игры, имеющей седловую точку, является игра с платежной матрицей.

В данной матрице минимальные (гарантированные) вы­игрыши первого игрока по строкам равны 1, 5 и (-3). Следовательно его максиминному выбору будет отвечать стратегия 2, гарантирующая выигрыш 5. Для второго игрока макси­мальные проигрыши по столбцам матрицы составят 8, 10, 5, 17, поэтому имеет смысл остановиться на стратегии 3, при ко­торой он проиграет только 5. Таким образом, вторая страте­гия первого игрока и третья стратегия второго образуют сед­ловую точку со значением 5, т. е. игра с матрицей имеет решение (2; 3; 5).

16. Методи обчислення власних векторів та власних чисел лінійних операторів. Рассматриваемые здесь алгоритмы предназначены для поиска собственных значений матрицы A, т.е. вычисление корней характеристического уравнения

Проблема же нахождение соответствующих собственных векторов является более простой, так как если корни характеристического уравнения известны, то задача сводится к отысканию не нулевых решений некоторых однородных линейных систем.

Основной прием использующийся при отыскании собственных значений матрицы это развертывание определителя в полином n-й степени. Отыскание же корней полученного полинома является отдельной, отнюдь не тривиальной задачей. Здесь могут пригодится методы из раздела Полиномиальные и трансцендентные уравнения..

Следует заметить, что попытка решение задачи развертывания определителя в полином "в лоб", требует значительных вычислений, и весьма трудоемка. Нетрудно показать, что непосредственное вычисление коэффициентов характеристического полинома эквивалентно вычислению 2ⁿ-1 определителей различных порядков.

Из приведенных здесь методом наилучшую скорость при больших n показывает метод Данилевского, поэтому именно ему уделено наибольшее внимание. Единственным недостатком данного метода на мой взгляд является необходимость для некоторых матриц использовать рекурсивный вызов.

Нахождение собственных значений матрицы методом А.M. Данилевского.

Сущность метода Данилевского заключается в приведении векового определителя к так называемому нормальному виду Фробениуса

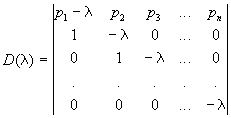
    Если нам удалось записать вековой определитель в такой форме, то, разлагая его по элементам первой строки будем иметь:

    Таким образом задача сводится к нахождению матрицы P в форме Фробениуса подобной матрице A, так как собственные числа инвариантны относительно операции подобия.     Процедура последовательно преобразует строки исходной матрицы, начиная с последней, к виду описанному выше, при этом преобразование осуществляется таким образом, чтобы полученные матрицы были подобны.     Опишем первое из преобразований, которое приводит n-ую строку исходной матрицы A к необходимому виду. Вначале преобразуем матрицу A в матрицу B по следующим формулам:

b_{i j}=a_{i j} - a_{i n-1}a_{n i} / a_{n n-1} при i=1,..,n; j не равно n-1;

b_{i n-1}=a_{i n-1} / a_{n n-1}, при i=1,..,n

Последняя строка построенной матрицы B будет удовлетворять нашим условиям, но не будет подобна матрице A, поэтому проведем еще одно преобразование и получим матрицу С подобную A и сохраняющую последнюю строку:

с_{i j}=b_{i j} при i=1,..,n-2

c_{n-1 j}=a_{n 1}b_{1 j}+a_{n 2}b_{2 j}+ . . . +a_{n n}b_{n j} при j=1,...,n

    Таким образом получили матрицу С подобную A и с последней строкой как в матрице привеленного вида Фробениуса. Продолжая, преобразуем аналогично n-1 строку матрицы С и т.д.     Допустим, что при преобразовании матрицы A в матрицу Фробенниуса P мы пришли к матрице вида:

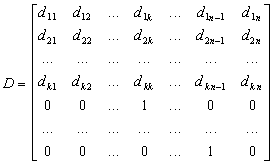
причем оказалось, что d_{k k-1}=0.     Тогда преобразования методом Данилевского нельзя продолжить. Здесь возможны два случая:    1. Существует элемент d_{k l} отличный от нуля, где l < k-1 , тогда переставляем местами (k-1) и l столбцы и (k-1) и l строки получаем матрицу подобную D для которой возможны дальнейшие преобразования по методу Данилевского.    2. Все элементы k строки равны нулю, тогда полученная матрица имеет вид:

Причем D₂ имеет нормальный вид Фробениуса, а матрицу D₁ можно привести к нему методом Данилевского. Полином же порождающий собственные значения матрицы А, есть произведение аналогичных полиномов для D₁ и D₂, при этом коэффициенты полинома для D₂ определены.     Процедура на вход получает матрицу A, а на выходе выдает матрицу C подобную A, при этом С имеет нормальный вид Фробениуса. Флаговая переменная S используется для определения случая когда дальнейшее преобразование не возможно, точнее: S=0 когда алгоритм успешно отработал, S > 0 когда на некотором шаге возник случай описанный в пункте 2, при этом S колличество строк в матрице D₁.

Нахождение собственных значений матрицы методом Леверрье.

Процедура определяет коэффициенты характерестического полинома

матрицы A. Положим:

тогда справедливы формулы Ньютона:

Отсюда получаем линеиную алгебраическую систему:

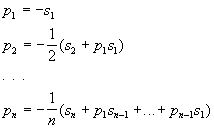
Из которой шаг за шагом определяются коэффицитенты p₁,...,p_n. Следует заметить, что s_k равен следу матрицы A^k, которая находятся непосредственным перемножением используя алгоритм умножения матриц.

Нахождение собственных значений матрицы методом неопределенных коэффициентов.

Процедура определяет коэффициенты характеристического полинома

матрицы A. Для этого полагаем в предыдущем равенстве =0,1,...,(n-1), таким образом получим систему из n линейных уравнений относительно p₁,...,p_n. Корни системы находим используя любой из методов.