9. Файловый ввод-вывод

Библиотечные подпрограммы Си для работы с файлами можно разделить на 2 группы - потоковые и префиксные. И те, и другие обращаются в принципе к одним и тем же вызовам MS DOS, но потоковые выполняют дополнительную буферизацию информации, что приводит к двойной буферизации - на уровне ОС и на уровне библиотечной подпрограммы.

Префиксные - это блок-ориентированные функции, обращающиеся к префиксным функциям ОС без дополнительной буферизации и их использование дает выигрыш в производительности при переносе сразу группы байтов за одно обращение к функции.

Для обеих групп функций файлового ввода-вывода возможны 2 режима доступа к файлу: текстовый и двоичный. В текстовом режиме производится трансляция символьных кодов 0DH, 0Ah - при чтении из файла в один символ новой строки ‘\n’, а при записи в файл этот символ преобразуется в пару CR LF; кроме того, при считывании символа Ctrl Z считается, что достигнут конец файла и прочитать информацию после этого символа в текстовом режиме не удается.

В двоичном режиме никакого преобразования байтов не происходит и не делается никаких предположений об их смысле.

Режим доступа к файлу задается при его открытии через параметры библиотечной функции или присвоением значения специальной внешней переменной _fmode, описанной в <fcntl.h> или <stdlib.h> и могущей принимать 2 значения: O_BINARY или O_TEXT(по умолчанию).

Потоковый ввод-вывод.

Поток (stream) - абстрактное понятие, связанное с переносом данных между устройством чтения-записи и потоком этих данных, “движущихся” мимо устройства (воображаемой головки). Потоком информации можно считать данные на диске или поступающие с клавиатуры или дисплей, или порты ввода-вывода - любое устройство с последовательной структурой информационных записей.

Для каждого файла, открытого для доступа через поток, Си создает внутреннюю структурную переменную по шаблону FILE.

Открытие файла:

FILE *f=fopen(const char * Filename, const char * mode);

Строка mode может принимать значения:

r - открыть для чтения

w - создать для записи с усечением

a - открыть для добавления в существующий файл

a+ - открыть для обновления или создать для чтения и записи

r+ - открыть файл для чтения и записи

w+ - открыть файл для чтения и записи

b двоичный режим

t текстовый режим

Общепринятая схема:

#include <stdio.h>

FILE *f;

main() { if((f=fopen("myFile.txt","r"))!=NULL... else...}

Закрытие файла:

int fclose(FILE*fp)

int fcloseall(void)

Переоткрытие файла с другими правами доступа:

FILE *freopen(const char *Filename, const char *mode, FILE *stream)

Открытие безымянного временного файла, уничтожаемого при закрытии или завершении программы: FILE *tmpfile(void)

Внимание! При задании имени файла с маршрутом доступа не забывайте ставить разделитель между именами каталогов в виде двойного обратного слэша:

c:\\dir1\\dir2\\Filem\\name или c:/dir1/dir2/Filem/name

Стандартные потоки: stdin, stdout, stderr, stdaux, stdprn являются указателями на переменные типа FILE и могут использоваться наравне с возвращаемыми функцией fopen.

Библиотеки Си содержат функции потокового посимвольного, построчного, блокового и форматированного ввода-вывода.

10, 13. Прямые методы решения систем линейных алгебраических уравнений. Метод решения задачи называют прямым, если он позволяет получить решение после выполнения конечного числа элементарных операций. Метод решения задачи называют итерационным, если в результате получают бесконечную последовательность приближений к решению. Если эта последовательность сходится к решению задачи, то говорят, что итерационный процесс сходится. К прямым методам решения относятся метод Гаусса и его модификации, метод Холецкого и метод прогонки. В методе Гаусса для вычисления масштабирующих множителей требуется делить на ведущие элементы каждого шага. Если элемент равен нулю или близок к нулю, то возможен неконтролируемый рост погрешности. Поэтому часто применяют модификации метода Гаусса, обладающие лучшими вычислительными свойствами. Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора). На k-ом шаге прямого хода в качестве ведущего элемента выбирают максимальный по модулю коэффициент при неизвестной в уравнениях с номерами i = k+1, ... , m.Затем уравнение, соответствующее выбранному коэффициенту с номером , меняют местами с к-ым уравнением системы для того, чтобы главный элемент занял место коэффициента . После этой перестановки исключение проводят как в схеме единственного деления. В этом случае все масштабирующие множители по модулю меньше единицы и схема обладает вычислительной устойчивостью.

Метод Холецкого. Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU-разложения матрицы A, в результате чего она приводится к виду A= . Если разложение получено, то как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами: и . Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам: , , i = 2, 3, ..., m,

, , i = 3, 4, ..., m,

...............

, , i = k+1, ... , m.

Метод прогонки. Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:

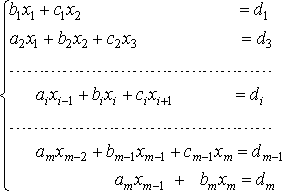
Преобразуем первое уравнение системы к виду , где , Подставим полученное выражение во второе уравнение системы и преобразуем его к виду и т.д. На i-ом шаге уравнение преобразуется к виду , где , . На m-ом шаге подстановка в последнее уравнение выражения дает возможность определить значение : . Значения остальных неизвестных находятся по формулам: , i = m-1, m-2, ..., 1.

Итерационные методы решения СЛАУ

Для решения задачи методом итераций система уравнений должна быть преобразована к виду:

x1k+1=f(x2k, x3k, ..., xnk), x2k+1=f(x1k, x3k, ..., xnk), ……………………… xnk+1=f(x1k, x2k, ..., xn-1k, xnk).

Итерационный процесс начинается при k=0 заданием начальных значений компонент вектора решения х (в общем случае произвольных); эти значения подставляются в правые части приведенных уравнений для вычисления следующего приближения, это следующее значение становится предыдущим, подставляется в систему для получения следующего и т.д. либо до достижения заданного приращения значений корней на очередной итерации, либо до выполнения заданного числа итераций. Это метод простых итераций. Его можно видоизменить, если в каждое следующее уравнение подставлять значения уже вычисленных компонент вектора решения:

x1k+1=f(x2k, x3k, ..., xnk), x2k+1=f(x1k+1, x3k, ..., xnk), ………………………. xnk+1=f(x1k+1, x2k+1, ..., xn-1k+1, xnk).

Эта модификация носит название метода Зейделя.

Сравнение прямых и итерационных методов

Системы линейных алгебраических уравнений можно решать как с помощью прямых, так и и итерационных методов. Для систем уравнений средней размерности чаще использют прямые методы.

Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограниченииий в доступной оперативной памяти ЭВМ или из-за необходимости выполнения черезмерно большого числа арифметических операций. Большие системы уравнений, возникающие в основном в приложениях, как правило являются разреженными. Методы исключения для систем с разреженным и матрицами неудобны, например, тем, что при их использовании большое число нулевых элементов превращается в ненулевые и матрица теряет свойство разреженности. В противоположность им при использованнии итерационных методов в ходе итерационного процесса матрица не меняется, и она, естественно, остается разреженной. Большая эффективность итерационных методов по сравнению с прямыми методами тесно связанна с возможностью существенного использования разреженности матриц. Применение итерационных методов для качественного решения большой системы уравнений требует серьезного использования ее структуры, специальных знаний и определенного опыта.

11. (Задача нелінійного програмування в 5 питанні.) Градиентные методы решения задач безуслов­ной оптимизации. Ведущее место среди прямых методов ре­шения экстремальных задач занимает градиентный метод (точнее, семейство градиентных методов) поиска стационар­ных точек дифференцируемой функции. Напомним, что стаци­онарной называется точка, в которой и которая в со­ответствии с необходимым условием оптимальности является «подозрительной» на наличие локального экстремума. Таким образом, применяя градиентный метод, находят множество точек локальных максимумов (или минимумов), среди которых определяется максимум (или минимум) глобальный.

Идея данного метода основана на том, что градиент функции указывает направление ее наиболее быстрого возрастания в окрестности той точки, в которой он вычислен. Поэтому, если из некоторой текущей точки х⁽¹⁾ перемещаться в направлении вектора , то функция f будет возрастать, по крайней мере, в некоторой окрестности х⁽¹⁾. Следовательно, для точки , , лежащей в такой окрестности, справедливо неравенство . Продолжая этот про­цесс, мы постепенно будем приближаться к точке некоторого локального максимума (см. рис. 2.1).

Однако как только определяется направление движения, сразу же встает вопрос о том, как далеко следует двигаться в этом направлении или, другими словами, возникает проблема выбора шага , в рекуррентной формуле

(2.8)

задающей последовательность точек, стремящихся к точке мак­симума.

В зависимости от способа ее решения различают различные варианты градиентного метода. Остановимся на наиболее изве­стных из них.

Метод наискорейшего спуска

Название метода можно было бы понимать буквально, если бы речь шла о минимизации целевой функции. Тем не менее, по тра­диции такое название используется и при решении задачи на максимум.

Пусть f(x) = f(x_l,x_l,...x_n) — дифференцируемая функция, заданная на Rⁿ, а — некоторая текущая точка. Оговоримся, что каких-либо общих рекомендаций, каса­ющихся выбора исходной точки (или, как еще говорят, началь­ного приближения) x⁽⁰⁾, не существует, однако по возможно­сти она должна находиться близко от искомого оптимального плана х^*. Как уже говорилось выше, если x^(q) — нестационарная точка (т. е. ), то при движении в направлении функция f(x) на некотором промежутке обязательно будет возрастать. Отсюда возникает естественная идея такого выбора шага, чтобы движение в указанном направлении продол­жалось до тех пор, пока возрастание не прекратится. Для этого выразим зависимость значения f(x) от шагового множителя  > 0 , полагая

(2.9)

или, в координатной форме,

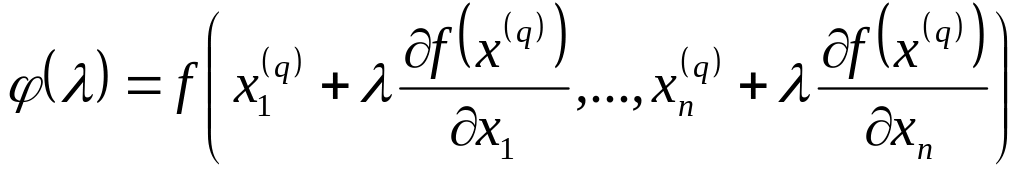(2.10)

Чтобы добиться наибольшего из возможных значений f при движении по направлению , нужно выбрать такое значе­ние , которое максимизирует функцию . Для вычисления , используется необходимое условие экстре­мума . Заметим, что если для любого  >0 , то функция f(x) не ограничена сверху (т. е. не име­ет максимума). В противном случае, на основе (2.10) получаем

(2.11)

что, в свою очередь, дает

(2.12)

Если считать, что следующая точка соответствует оп­тимальному значению , то в ней должно выполняться условие , и следует находить из условия или

(2.13)

Условие (2.13) означает равенство нулю скалярного про­изведения градиентов функции f точках х^(q+1) и х^(q) Гео­метрически оно может быть интерпретировано как перпендикулярность векторов градиентов функции f в указанных точ­ках, что и показано на рис. 2.2. Продолжая геометрическую интерпретацию метода наискорейшего спуска, отметим, что в точке х^(q+1) вектор , будучи градиентом, перпендику­лярен линии уровня, проходящей через данную точку. Стало быть, вектор является касательным к этой линии. Итак, движение в направлении градиента следует продолжать до тех пор, пока он пересекает линии уровня оп­тимизируемой функции.

После того как точка х^(q+1) найдена, она становится текущей для очередной итерации. На практике признаком достижения стационарной точки служит достаточно малое изменение коор­динат точек, рассматриваемых на последовательных итераци­ях. Одновременно с этим координаты вектора должны быть близки к нулю.