43. Методи розв'язування крайових задач системи звичайних диференціальних рівнянь. Різницеві схеми для рівнянь другого порядку. Методи прогонки.

Розглянемо задачу:

[0, 1] розіб'ємо на n частин, ,

Розглянемо розклади

Із (3),(4) одержимо

(5),(6),(7) – різницеві співвідношення, які апроксимують 1,2 похідну. Використовуючи різницеві співвідношення (5),(6),(7) апроксимуючи оператори L, l одержимо задачу:

Щоб порівнювати фунції u^(h) i u, f^(h) i f, введем норму

Означення 1:

Оператор L_h (l) апроксимує на функції u оператор L (l) з порядком апроксимації К, якщо , що має місце:

Означення 2:

f_h ( ) апроксимує f ( ) з порядком апроксимації К, якщо , що має місце:

Означення 3:

Різницева схема (8), (9) апроксимує крайову задачу (1), (2) з порядком апроксимації к, якщо виконуються умови (10-13).

Розглянемо апроксимацію оператора крайових або початкових умов.

Відзначимо, що розв'язок задачі (14-15) задовільняє і ряд тривіальних умов. Наприклад:

Оператор апроксимуєм різницевим оператором

Враховуючи, що , одержимо:

, тобто

Щоб одержати апроксимацію вищого порядку, треба використовувати тривіальні умови

Використаємо тривіальні умови для визначення ; із рівняння

Замість задачі (14), (15) можемо розглядати задачу

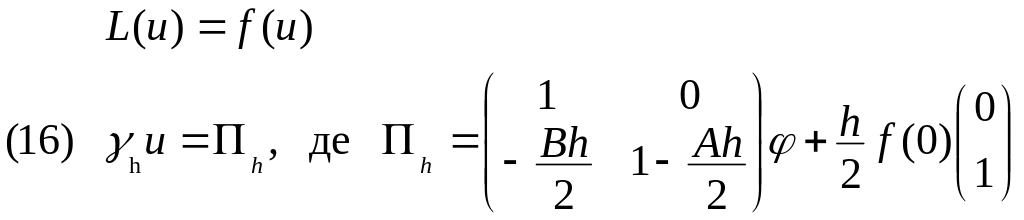
тому, що розв'язок задачі (14-15) однозначно визначається умовами (14), (16).

Для підвищення порядку апроксимації можна користуватись ще формулами:

Метод прогонки

Виберемо сітку х₀, х₁…х_N , x₀=a, x_n=b, h=(b-a)/n

Різницеву схему (3), (4) перетворимо до вигляду:

Розглянутий метод називається різницевим методом прогонки.

Якщо різницева задача (5),(6) має вигляд:

То проводячи аналогічні викладки одержимометод правої прогонки, якщо

то метод буде стійким до похибки округлень

Якщо виконуються умови:

то можна застосовувати метод лівої прогонки, який буде стійкий до похибок заокруглень

44. Повні системи булевих функцій та базиси.

Одна й теж сама логічна функція може бути задана декількома формулами, які містять різні набори логічних операцій . Існують набори логічних функцій, за допомогою яких можна виразити будь-яку іншу функцію алгебри логіки . Такі набори (системи) називаються повними системами функцій алгебри логіки, або базисами.

Означення 1.12. Система булевих функцій } називається функціонально повною, якщо будь-яка булева функція може бути записана у вигляді формули через функції цієї системи.

Як приклад повної системи, можна навести систему, яку складають всі булеві функції. Кількість функцій – . Так, усі 16 функцій двох змінних утворюють повну систему.

Повні набори (системи) функцій характеризуються певним набором властивостей функцій, які є її складовими.

Приклад 1.20. Наведемо приклади повних систем, використовуючи позначку інверсії :

1. ; 2. ; 3. ;

4. ; 5. ; 6. ;

7. ;    

Справедливе таке твердження :

Будь-яка функція алгебри логіки може бути задана формулою за допомогою диз’юнкції, кон’юнкції й заперечення. Із цього випливає, що система функцій  є функціонально повною.

Таким чином, для доведення функціональної повноти будь-якої системи функцій достатньо показати, як можна виразити  за допомогою функцій цієї системи.

Або навпаки, для доведення функціональної повноти будь-якої системи функцій, достатньо показати, як можна виразити функції цієї системи за допомогою операцій .

Приклад 1.21. Щоб довести повноту системи  із п.2 прикладу 1.20 достатньо показати, що операція  може бути виражена через  і , а щоб довести повноту системи  із п.3 прикладу 1.20 достатньо показати, що операція  може бути виражена через  і .

Це можна зробити за допомогою вже відомих вам законів де Моргана:

;

.

Повнота системи , яка складається із однієї операції штрих Шиффера, і системи , яка складається із однієї операції стрілка Пірса, доведено в попередньому параграфі.

В табл.1.11 наведені властивості булевих операцій , які є аналогічними властивостям звичайних алгебраїчних операцій додавання, віднімання, множення і ділення над числами. Множина значень 0 і 1, яких набувають булеві змінні, разом з операціями  утворюють булеву алгебру. Основними властивостями операцій булевої алгебри є властивості наведені в табл.1.11. Перетворення булевих формул згідно табл.1.11 називається алгебраїчними перетвореннями.

Виникає питання, навіщо потрібне поняття повноти системи булевих функцій. Відповідь полягає в наступному. Виходячи з деяких міркувань, можна обрати деяку повну систему і тоді будь-яку формулу представити за допомогою функцій обраної системи. Наприклад, в мікросхемотехніці завдяки простоті реалізації обирають систему . Крім того, обрана повна система дозволяє робити перехід від табличного подання булевих функцій, до подання у вигляді формули.