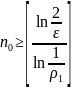- •Обчислювальний експеримент. Теорія попиту.
- •Абсолютна і відносна похибки
- •Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
- •Метод Гауса чисельного розв’язку слр.
- •Вивід розрахункових формул
- •Модифікація методу Гауса
- •Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
- •Обчислення визначника
- •Обчислення обернених матриць
- •Обумовленість с-ми лінійних рівнянь Стійкість слар
- •Обумовленість слар, число обумовленості
- •Метод прогонки для розв’язання слар
- •Ітераційні методи розв’язання слар
- •Ітераційний метод Якобі
- •Ітераційний метод Зейделя
- •Канонічна форма однокрокових ітераційних методів
- •Приклад розв’язання методом Зейделя та Якобі
- •Метод простої ітерації
- •Дослідження збіжності ітераційних методів
- •Необхідна і достатня умова збіжності у стаціонарних методах
- •Оцінки швидкості збіжності стаціонарних ітераційних методів
- •Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
- •Многочлен Чебишева на проміжку [a,b]
- •Ітераційні методи Чебишовським набором параметрів
- •Неявний Чебишевський ітераційний метод
- •Інтерполяція функцій
- •Інтерполяційний многочлен Лагранжа
- •Розділені різниці. Інтерполяційний многочлен Ньютона
- •Властивості розділених різниць
- •Побудова інтерполяційного многочлена Ньютона
- •Приклад
- •Скінченні різниці
- •Формула залишкового члена інтерполяційного многочлена Лагранжа
- •Інтерполяції за допомогою раціональних функцій
- •Інтерполювання періодичних функцій
- •Інтерполяційний многочлен Ерміта
- •Збіжність інтерполяційних процесів
- •Інтерполяція сплайнами
Многочлен Чебишева на проміжку [a,b]
Іноді виникає потреба побудови многочлена Чебишева на проміжку [a,b]

 ,
,  ,
,
 ,
, 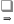
 (1)
(1)

 (2)
(2)
Причому
коефіцієнт при
 буде рівна
буде рівна

Тоді многочлен Чебишева із старшим коефіцієнтом «1», який найменше відхиляється від нуля
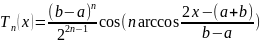 (3)
(3)
Це многочлен першого роду на проміжку [a,b], тоді відповідно корені цього многочлена :


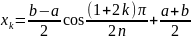 (4)
(4)  -
корені
-
корені
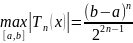
В теорії чисельних методів виникає задача:
Знайти
многочлени, які найменше відхиляються
від нуля на [a,b].
Це многочлени n-го
степеня, які при
 рівні
одиниці. Вигляд такого многочлена може
бути записаний
рівні
одиниці. Вигляд такого многочлена може
бути записаний
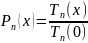 (5)
(5)
 , тоді із рівностей (3) і (5) ми одержимо
, тоді із рівностей (3) і (5) ми одержимо
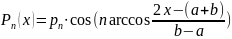 (6)
(6)
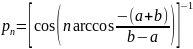 (7)
(7)
Введемо в розгляд заміну змінної
 ,
,
 ,
,


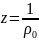

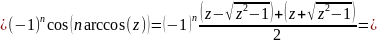 :::
:::
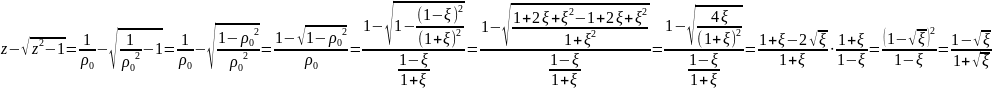

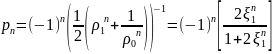 ,
де
,
де
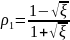
Серед всіх многочленів степеня (n) які при приймають значення «1» і найменше відхиляються на прміжку [a,b] від нуля.

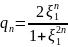 ,
,
,
,
,
,
Також ставиться інша задача, яка розглядається при виборі оптимальних параметрів для цілих процесів
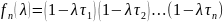 (9)
(9)
 підбираємо таким чином щоб мінімізувати
величину
підбираємо таким чином щоб мінімізувати
величину
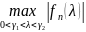 .
Многочлен
(9) задовольняє умову
.
Многочлен
(9) задовольняє умову
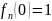 .
Цю задачу можна вирішити за допомогою
многочлена Чебишева(8). Корені (9) :
.
Цю задачу можна вирішити за допомогою
многочлена Чебишева(8). Корені (9) :

 тоді ці корені
повинні співпадати з коренями многочлена
(8)
тоді ці корені
повинні співпадати з коренями многочлена
(8)

Тоді,
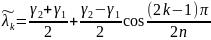 ,
,
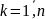
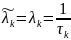 і тоді відхилення
від нуля буде мінімальним
і тоді відхилення
від нуля буде мінімальним

Ітераційні методи Чебишовським набором параметрів
Розглянемо
СЛАР виду
 (1) з симетричною додатньовизначеною
матрицею А. будемо розв’язувати систему
(1) за допомогою явного нестаціонарного
ітераційного методу.
(1) з симетричною додатньовизначеною
матрицею А. будемо розв’язувати систему
(1) за допомогою явного нестаціонарного
ітераційного методу.
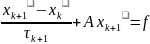 (2) де
(2) де
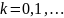 – початкове наближення
– початкове наближення
Поставимо
задачу про вибір оптимальних параметрів,
тобто в відшуканні таких чисел
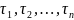 в яких
в яких
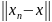 буде мінімальною
буде мінімальною
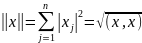 ,
де
,
де
 –
–
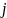 -а
компонента
-а
компонента
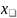
Теорема_1.
Нехай
матриця А симетрична додатньовизначена
і
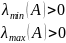 є відповідними min
і
max
власним значенням, і нехай задано число
ітерацій n,
тоді серед методів типу (2)
найменшу
похибку
має метод для якого
є відповідними min
і
max
власним значенням, і нехай задано число
ітерацій n,
тоді серед методів типу (2)
найменшу
похибку
має метод для якого
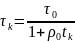 ,
,
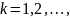
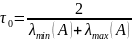
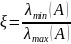 (4)
(4)
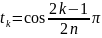
Тоді
якщо параметр
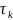 вибираєм з (3) і (4) то для похибки буде
справедлива оцінка.
вибираєм з (3) і (4) то для похибки буде
справедлива оцінка.
 (5)
(5)
 ,
,
,
,
Доведення.
Позначимо через
 де k
– точний розвязок
де k
– точний розвязок
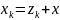
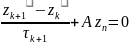 (7)
(7)
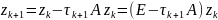
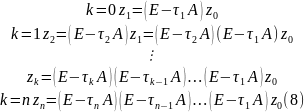
 (9)
(9)
(8):


Так
як E
і A
є симетричні
то
 також є симетричною і норма симетричної
матриці співпадає з її спектральним
радіусом, тобто з найбільшим власним
значенням по модулю, тоді
також є симетричною і норма симетричної
матриці співпадає з її спектральним
радіусом, тобто з найбільшим власним
значенням по модулю, тоді

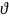 максимальне власне
значення матриці
максимальне власне
значення матриці
Тоді
треба так параметр
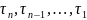 так щоб
так щоб
 було найменшим. Нехай власні значення
матриці А
розташуєм
їх у порядку
було найменшим. Нехай власні значення
матриці А
розташуєм
їх у порядку
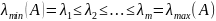 то власні значеня для матриці
будуть
відповідно числа
то власні значеня для матриці
будуть
відповідно числа
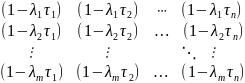
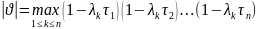
Треба вибрати та параметр щоб було мінімальним
 (10)
(10)

, тому ця задача розвязується за допомогою многочленів Чебишева. Корені многочлена (10) і вони повинні співпадати з коренями многочлена
 (11)
(11)
, , (12)
Тоді корені многочлена будуть знаходитись в точках
 (13)
(13)
То
відхилення
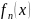 від нуля буде мінімальним і таке
максимальне відхилення буде дорівнювати
від нуля буде мінімальним і таке
максимальне відхилення буде дорівнювати
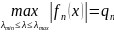 (14)
де
(14)
де
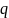 визначається
з (12)
визначається
з (12)
,
Доведено.
Знайдемо
кількість ітерацій які необхідні для
досягнення деякої точності

З нерівності(5):
 ,
де
визначається
з (12)
,
де
визначається
з (12)
 ,
,
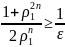 ,
,

 ,
,
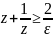 ,
,
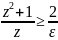 ,
,
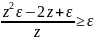
 ,
,
 ,
,

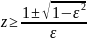 ,
,
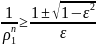
 ,
,

З (15) вибираємо кількість ітерацій яка необхідна для досягнення зданої точності .