
- •Обчислювальний експеримент. Теорія попиту.
- •Абсолютна і відносна похибки
- •Методи розв’язання системи лінійних рівнянь (слр). Прямі методи слр.
- •Метод Гауса чисельного розв’язку слр.
- •Вивід розрахункових формул
- •Модифікація методу Гауса
- •Умови застосування методу Гауса і його зв'язок з розкладом матриці на множники.
- •Обчислення визначника
- •Обчислення обернених матриць
- •Обумовленість с-ми лінійних рівнянь Стійкість слар
- •Обумовленість слар, число обумовленості
- •Метод прогонки для розв’язання слар
- •Ітераційні методи розв’язання слар
- •Ітераційний метод Якобі
- •Ітераційний метод Зейделя
- •Канонічна форма однокрокових ітераційних методів
- •Приклад розв’язання методом Зейделя та Якобі
- •Метод простої ітерації
- •Дослідження збіжності ітераційних методів
- •Необхідна і достатня умова збіжності у стаціонарних методах
- •Оцінки швидкості збіжності стаціонарних ітераційних методів
- •Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
- •Многочлен Чебишева на проміжку [a,b]
- •Ітераційні методи Чебишовським набором параметрів
- •Неявний Чебишевський ітераційний метод
- •Інтерполяція функцій
- •Інтерполяційний многочлен Лагранжа
- •Розділені різниці. Інтерполяційний многочлен Ньютона
- •Властивості розділених різниць
- •Побудова інтерполяційного многочлена Ньютона
- •Приклад
- •Скінченні різниці
- •Формула залишкового члена інтерполяційного многочлена Лагранжа
- •Інтерполяції за допомогою раціональних функцій
- •Інтерполювання періодичних функцій
- •Інтерполяційний многочлен Ерміта
- •Збіжність інтерполяційних процесів
- •Інтерполяція сплайнами
Необхідна і достатня умова збіжності у стаціонарних методах
 (4)
(4)
Система (4) є
однорідною відносно (3). Ітераційний
метод буде збігатися якщо
 .
Рівність (4) перепишемо в іншому виді
.
Рівність (4) перепишемо в іншому виді
 (5)
(5)

S- матриця перходу від n-ї до n+1 ітерації, тоді справедлива теорема.
Теорема
Ітераційний метод
(3) збігається при будь-якому початковому
наближенні тоді і тільки тоді, якщо всі
власні значення матриці S

Оцінки швидкості збіжності стаціонарних ітераційних методів
У попередній теоремі показано, що для дослідження збіжності ітераційного методу необхідно досліджувати всі власні значення матриці або володіти інформацією про спектр матриці. Для оцінки ітераційних методів важливим є не тільки факт збіжності, але й швидкість збіжності з яким метод збігається до точного розвязку. Так як ітераційний метод здійснюється за скінченну кількість кроків, то нам необхідно знати у скільки разів зменшиться початкова похибка після проведеного числа ітерацій.
Будемо говорити,
що метод збігається із швидкістю
геометричної прогресії, якщо виконується
така нерівність

 (7)
(7)
Оцінку (7) можна
використати для визначення кількості
операцій для того щоб початкова похибка
зменшувалася задане число разів. Введемо
число
 і будемо вимагати
і будемо вимагати
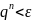


 (8)
(8)
Із (8)
бачимо, що після виконання
 ітерацій виконується нерівність
ітерацій виконується нерівність
 (9)
(9)
Після виконання
(9) і початкова похибка зменшиться на
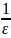 разів, тоді
- найменша кількість кроків, при яких
зменшується початкова похибка, а
разів, тоді
- найменша кількість кроків, при яких
зменшується початкова похибка, а
 –швідкість збіжності ітераційного
методу. Тоді швидкість збіжності повністю
визначає властивості матриці S
і не залежить від номера ітерації і від
вибору початкового наближення. Чим вища
швидкість збіжності, тим кращий
ітераційний метод, тому якість методів
прийнято порівнювати по їх швидкості
збіжності.
–швідкість збіжності ітераційного
методу. Тоді швидкість збіжності повністю
визначає властивості матриці S
і не залежить від номера ітерації і від
вибору початкового наближення. Чим вища
швидкість збіжності, тим кращий
ітераційний метод, тому якість методів
прийнято порівнювати по їх швидкості
збіжності.
Теорема 1
Нехай матриці А і В є симетричними і додатньовизначеними і для неї справедлива нерівність
 (10),
де
(10),
де

 , тоді при
, тоді при
 (11) ітераційний
метод (3) є збіжним і для похибки будуть
справедливі оцінки
(11) ітераційний
метод (3) є збіжним і для похибки будуть
справедливі оцінки
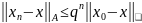



 (14)
(14)
Зауважимо,
що найбільш точними константами при
 при яких виконується нерівність (10)
являється
при яких виконується нерівність (10)
являється


 -оптимальний
параметр бо мінімізує вираз (14)
-оптимальний
параметр бо мінімізує вираз (14)
Наслідокю
розглянемо
метод простої ітерації



Многочлени Чебишева 1-го роду і многочлени Чебишева на відрізку [0,1]
В багатьох задачах чисельного аналізу ми зіштовхуємось з проблемою мінімізації похибки обчислювального алгоритму. Для мінімізації похибки ми будемо використовувати властивості многочлена Чебишева, тобто многочленів які мало відрізняються від нуля.
Задача.
Серед всіх многочленів n-го степеня з
старшим коефіцієнтом 1 знайти такий
многочлен
 для якого
для якого
 буде мінімальною. Многочлен який володіє
такою властивістю називається многочленом,
який якнайменше відмінний від нуля на
проміжку [-1,1]. Покажемо що многочлен
виду
буде мінімальною. Многочлен який володіє
такою властивістю називається многочленом,
який якнайменше відмінний від нуля на
проміжку [-1,1]. Покажемо що многочлен
виду
 являється многочленом Чебишева.
Розглянемо многочлен
являється многочленом Чебишева.
Розглянемо многочлен
 (2). Для такого многочлена
(2). Для такого многочлена
 можемо записати
можемо записати

 (3)
(3)



Із
(3) :
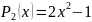

Многочлен
– многочлен
n-го
степення із старшим коефіцієнтом « »
де
»
де

Запишемо властивості многочлена
Для
 - многочлен
n-го
степеня з старшим коефіцієнтом
- многочлен
n-го
степеня з старшим коефіцієнтом
Многочлени
 степеня є парними функціями
степеня є парними функціями
Многочлен ( )
степеня є
непарними функціями
)
степеня є
непарними функціями

 парні
парні

 непарні
непарні
Із (3) :
 – парна
– парна
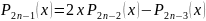 – непарна
– непарна
Многчлен має n дійсних коренів на [-1,1]



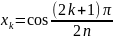
Многочлен приймає свої найбільші значення на проміжку [-1,1] в точках




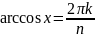

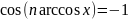




Тоді
многочлен
також є многочленом n-го степеня з із
старшим коефіцієнтом «1».
Корені
будуть розміщені в точках (4)
 де
де
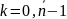 , а екстремуми
будуть знаходитись в точках (5)
, а екстремуми
будуть знаходитись в точках (5)
 .
.
При
чому
 (6)
(6)
 і відповідно
і відповідно
 (7)
(7)
Доведемо,
що серед многочленів степеня n із старшими
коефіцієнтами «1». Многочлен
найменше відхиляється від нуля на
проміжку [-1,1].
Введемо в розгляд многочлен
 степення
n
із старшими
коефіцієнтами «1». Введемо в розгляд
позначення
степення
n
із старшими
коефіцієнтами «1». Введемо в розгляд
позначення

Лема.
Нехай
система точок
 (8)
(8)
 (9) при чому
(9) при чому
 )
почергово міняє знак на проміжку [-1,1] ,
тоді серед всіх многочленів n-го степення
з старшими коефіцієнтами «1» многочлен
)
почергово міняє знак на проміжку [-1,1] ,
тоді серед всіх многочленів n-го степення
з старшими коефіцієнтами «1» многочлен
 якнайменше відхиляється від нуля.
якнайменше відхиляється від нуля.
Із умов (6) і (7) многочлен ,буде задовольняти умовам Леми і тому такий многочлен буде многочленом k-го степеня з старшим коефіцієнтом «1» який якнайменше відрізняється ві нуля.
