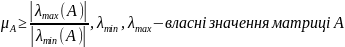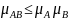Обчислення визначника

Одночасно з розв’язанням системи при застосуванні методу Гаусса шукають визначник матриці А.

; ,

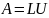
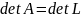
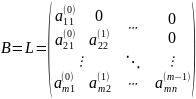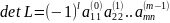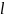- кількість перестановок рядків при відшуканні матриці L. Якщо ж матриця А є виродженою, тоді при використанні методу Гаусса на деякім k – кроці з вибором елемента у стовпці всі елементи k – го стовпця що знаходиться нижче головної діагоналі і на головній діагоналі будуть = 0.

Тоді при застосуванні методу Гаусса повинна виконуватись перевірка

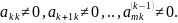
1. Якщо хоча б один з цих елементів 0, то система може бути розв’язана методом Гаусса;

2. Якщо всі = 0, тоді розв’язання за методом Гаусса припиняється.

Обчислення обернених матриць

Відшукання обернених матриць еквівалентне розвязку рівняння (1)

(1)

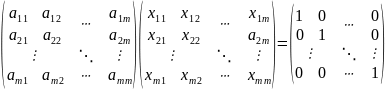(2)

Введем позначення

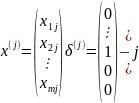
Розв’язання системи (2) еквівалентне розв’язанню m-систем (3)

При розвязанні кожної такої системи ми одержимо відповідний стовпець шуканої матриці.

Обумовленість с-ми лінійних рівнянь Стійкість слар

Під коректністю будемо розуміти, що розвязок поставленої задачі існує, він єдиний і неперервно залежить від початкових умов.

Будемо досліджувати с-му 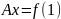. Задача буде корректно поставлена, коли матриця невироджена. Для встановлення неперервної залежності треба виділити:

1. Що є вхідними даними для даної задачі;

2. В якому сенсі розрізняти цю неперервну залежність.

Вхідними для даної задачі є будемо розрізняти стійкість у правій частині, коли матриця А є незмінна і вектор 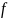має деякі зміни(збурення).

Стійкість коефіцієнта : коли - незмінний, змінні коефіцієнти матриці А.

Дослідимо стійкість у правій частині, коли -збурений. Зазвичай для задач які виникають із життя вектор не завжди можна точно отримати, тоді дивимось, яка неперервна залежність вхідних даних .

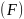Для визначеня неперервної залежності введемо поняття норми для m-вимірних векторів. Простір називається нормованим, якщо кожному 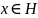ставиться у відповідність деяке дійсне число, яке називається нормою 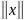і має задовольняти аксіомам норми:

1. ;

2. 

3. 

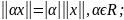
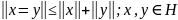
Найчастіше вживані норми:

;

;

;

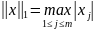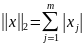Нормою матриці 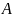наз. Таке число яка підпорядкована вектору x.

Матрична норма – максимум:

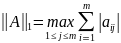
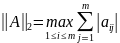
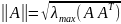
Властивості норми матриці:

1. 

2. 

3. ;

4. 

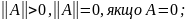
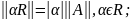
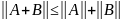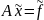(3) - система яка отримана з системи (1) зазнавши змін в правій частині.

Розв’язок буде називатися стійким, якщо для 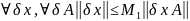(4) , де 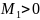і ця стала незалежить від правих частин, тоді нерівність (4) буде виражати факт неперервної залежності розвязку від правої частини, тобто якщ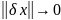о то .

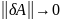Якщо 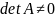, то с-ма (1) буде стійкою по правій частині. Із р-нянь (1) і (3) можемо записати с-му для похибок (5)

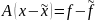
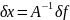
(6)

нерівність (6) еквівалентна (4)

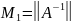
нерівність (6) показує стійкість системи із матрицею 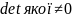відносно збурень правої частини. Відмітимо, чим ближче 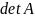до нуля тим більш точною є М1 і тим сильніша похибка правої частини може впливати на розвязок.

Обумовленість слар, число обумовленості

Розв’яжемо як зв’язні відносні похибки розвязку правої частини

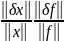
Перемножимо нерівності (6) і (7)

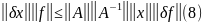
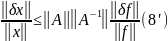
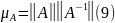
Число , яке виражене в (9) і входить в оцінку (8’) називається числом обумовленості матриці А. Це число характеризує ступінь залежності відносної похибки розв’язку від відносної похибки правої частини. Якщо число обумовленості є достатньо великим, то такі матриці називають погано обумовленими. На випливає також розмірність матриці і при чисельному розв’язанні систем з погано обумовленими матрицями можливе сильне накопичення похибки.

Властивості числа обумовленості:

1. 

2. 

3. 

Розглянемо систему, у якій збережена не тільки права частина, а і матриця А.

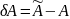
Теорема

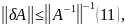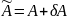Нехай матриця А має обернену і викнується нерівність тоді матриця має також обернену матрицю і тоді для відносної похибки розвязку буде справедлива нерівність