Обчислювальний експеримент. Теорія попиту.

Ефективне розв’язання задач,які виникають у реальному житті неможливе без використання ЕОМ. У теперішній час вироблена технологія дослідження складних систем, яка базується на побудові і аналізі за допомогою ЕОМ математичних моделей об’єктів, що вивчаються. Такий метод ––дослідження дістав назву обчислювального експерименту.

На першому етапі при розгляді деякого реального об’єкту даний об’єкт формується у математичних термінах (системи лінійних, системи нелінійних, диференційованих рівнянь ), іншими словами формується математична модель об’єкту.

На другому етапі математична модель перетворюється до такого виду, щоб в неї входили тільки ті операції, які може виконувати ЕОМ. Такі перетворення можуть здійснюватись за допомогою чисельних методів (методів обчислень). І тоді наслідок такого перетворення ми дістаємо модель, яку називають дискретною.

На третьому етапі складається програма реалізації. На четвертому етапі – підлагоджуємо роботу програми.

На п’ятому етапі – обробка результатів обрахунків ЕОМ з порівнянням з реальним об’єктом, на основі чого робиться висновок про відповідність або адекватність складеної моделі з реальним об’єктом.

Реальний об’єкт

Математична модель

Дискретна модель

Програмна реалізація

Відлагоджувана програма

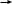
Модель – метод – програма

Предметом вивчення чисельних методів є вивчення одного з етапів обчислювального експерименту, тобто побудова і дослідження чисельного методу.

Процес дослідження об’єкту методом математичного моделювання і чисельного експерименту носить наближений характер,тому на кожному етапі вносяться ті або інші похибки.

Абсолютна і відносна похибки

а – наближене значення числа А,якщо число а не дуже відрізняється від значення числа А і може замінити його в обчисленні.

Тоді абсолютною похибкою наближеного числа а називається рівність ∆=│А-а│ (1)

Відносною похибкою наближеного числа а називається рівність 𝛿 ∆/А

Похибки виникають при чисельних розв’язаннях реальних задач із використанням математичного апарату. Ці похибки можна розділити на 5 груп:

1) Похибка задачі. Ці похибки пов’язані із самою постановою задачі. При побудові математичної моделі неможливо врахувати всі фактори,що впливають на розв’язок задачі,тому деякими доводиться нехтувати або приймати деякі припущення,цим самим спрощується задача і приводить до похибки.

2) Похибка методу. Інколи задачі складні у формулі,які заміняємо на близькі їм за результатами задачі (диференційоване рівняння заміняється різницевим).

3) Залишкові похибки. Ці похибки виникають у зв’язку з наявністю нескінченних процесів у математичному аналізі. Обривання нескінченних процесів породжує ці похибки.

4) Початкові похибки. Виникають коли ми деякі фізичні константи замінюємо наближеними значеннями(число е,π…).

5) Заокруглені похибки.

Х=±Мrр

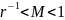
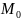- найменше дійсне число,яке може бути представлене у вигляді з плаваючою крапкою.

- машинний нуль

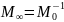- машинна нескінченність

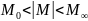
Похибка розв’язку задачі, яка виникає через неточність початкової інформації називається неусувною похибкою.

Неусувними похибками є похибка задачі і початкової похибки.

При вибраному чисельному методі залишається широка свобода у виборі алгоритму. Так як для зображення чисел використовується обмежена кількість десяткових розрядів, то під час проведення експерименту не вдається уникнути похибок заокруглення. Виявлено,що деякі алгоритми є чутливими до похибок заокруглення і у випадку застосування такого алгоритму одержана похибка на будь-якому етапі може сильно нагромаджуватись і ми одержимо велику похибку результату. Такі алгоритми є нестійкими.

Алгоритми, в яких допущена похибка на одному із кроків не нагромаджується прийнято називати стійкими.