11. Проективний простір. Принцип двоїстості. Т. Дезарга

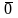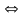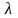О.: Нехай Р – мн елементів довільної природи. Мн Р наз проективним простором, якщо існує таке відображення П: V|{ } Р, що задовольняє умови: 1) П – сюрєкція 2) П(х)=П(у) х= у , 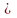0. 2 осн моделі:

1. Модель пучка. Зафіксуємо на Евкл пл. т. О-центр пучка і співставимо кожному ненульовому вектору пл. пряму, що прох через т.О // цьому вектору. Одержимо пучок прямих ­Е, який задов озн проект простору розмірності 1(кожна пр має напрямний вектор) 2.Модель розширеної прямої. Зафікс на евкл пл. пряму d, т. .Визначимо проект пр з пучком з центром в т.О.Співставимо прямим пучка їх точки перетину з d.Поставимо прямій пучка у відпов невласну т.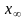 і доповнемо цією т. пр d. .Принц двоїстості. Розгл т.А(а₁,а₂,а₃)і т.В(в₁,в₂,в₃).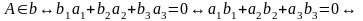

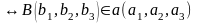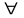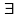–відношення інцедентності.1 малий принцип: якщо в твердженні про точки,пр і їх інцедентність на проект пл. поміняти місцями слова т. та пр. то одержимо твердж. вихідному твердж. Прикл.:на проект пл. безліч т. – на проект пл. безліч пр. 2. Великий: в твердж. про інцидент. точок,прямих і пл., слово т. можна замінити на пл. і навпаки.Прикл.: якщо пр пл. то вона перет її в 1 т. – через т. і пр. поза нею проходить єдина пл..

О: тривершин. наз фігура,що склад з 3-х т. загального положення і 3-х пр., які їх попарно сполуч. Знайдемо двоїсту фігуру до 3-вершинника. 3-вершинник двоїстий сам собі за малим принципом 2. інколи двоїсту фігуру на до 3-вер наз 3-сторонником. дана фігура: точок 3, прямих 3, через кожні 2 точки проходить 1 пряма, 2 пр перетинаються в 1 т. ДВОЇСТА ФІГУРА: прямих 3, точок 3, через 2 пр проходить 1 т, 2 т перет в 1 пр.

Т. Дезарга: якщо пр.,що сполуч відпов вершини 2-х триверш. в 1т., то прямі, які містять відповідні сторони тривірш, перетинаються в точках, які лежать на 1 пр. ДОВ: нехай А,В,С і А^/,В^/,С^/ - тривершинник, А і А^/ , В і В^/, С і С^/ відповідні. Нехай виконується умова теореми. Т. О є АА^/ , О є ВВ^/, О є СС^/. Розглянемо т. А, А^/ , О – колінеарні, породжуються П(а)=А, П(а^/)=А^/ . П(0)=0, вектори а не = а^/, отже, вони утворюють базис векторного простору. Тоді 0=л₁а+л₂а^/. (1) аналогічно 0=м₁в+м₂В^/,(2) 0=v₁c+v₂c^/.(3)

(1)-(2), (2)-(3), (3)-(1) . л₁а+л₂а^/- м₁в+м₂В^/=0, м₁в+м₂В^/- v₁c+v₂c^/=0, v₁c+v₂c^/- л₁а+л₂а^/=0. л₁а- м₁в= м₂В^/- л₁а=р, м₁в- v₁c= v₂c^/- м₂В^/=n, v₁c- л₁а= л₂а^/- v₂c^/=m. П(р)=Р, П(n)=N, П(m)=М. р+ n+ m=0. (біля всіх 0 вектори стоять). А отже, всі точки М, N, Р лежать на 1 прямій, що й треба було довести.

12. Група проективних перетворень площини. Аналітичний запис

О: проективним пертворенням ф наз таку відповідність між точками проективних просторів, при якому 4 т. 1 пр переходять у 4 т. іншої прямої і при цьому зберігається складне відношення 4 т. якщо при цьому відобр точки що леж на 1 пр.

Т: - репери на проект пл. тоді єдине проект перетв пл.,т.що 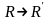Дов: Існування: співставимо кожній т.М(х₁,х₂,х₃)_R т.M’(x₁,x₂,x₃)_R’ і познач -перетворення. Покажемо що задов умові теореми. R з коорд (1,0,0);(0,1,0);(0,0,1);(1,1,1).Образами цих т. будуть т. з коорд.. але в R’.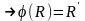 Єдиність: припуст що 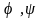-проект перетв пл. які задов умові теореми 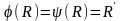. Розгл пр А₁А₂ і нех Е₃=А₁А₂ А₃Е тоді за умовою ,

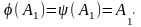де 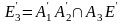Розгл т.М на пр А₁А₂ і позначемо 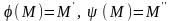.За означ зберігає відношення 4-ох точок:

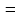
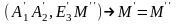.Розгл випадок т.М міститься поза коорд прими.Через т.М проведемо пр яка перетне коорд вісі в точках P,Q,R-лежать на коорд вісях

. Якщо ж 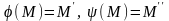одержимо

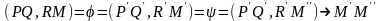Отже

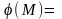
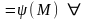т.М пл., отже 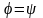Доведено

Щоб одержати ф-ли аналіт задання скорист попер теоремою тоді аналог до випадків рухів і афінних перетв пл. одержимо:

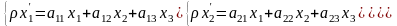.В матричному вигляді: ,де

А-матриця переходу, - коеф пропорційності.

Познач 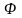- м-ну всіх проект перетвор пл.. Задамо на Ф композицію перетворень і покажемо що побудована алгебра є групою: 1. композиція перетворень є асоціативною операцією, отже і проект перетворень теж 2. тотожнє перетворення є проект і відіграє роль нейтрального елемента. 3. перетворення обернене до проективного є проективним. 4. композиція проект перетв є проект перетворенням так як при виконанні 2-ох проект перетв послідовно не зміниться а ні належність точок до пр а ні їх складне відношення. Таким чином маємо групу проект перетв пл.