8. Група рухів площини. Задання рухів.

О:Перетворення площ., яке зберіг. Відстані між точками наз. Рухом площини.Рухи:тотожні перетворення, паралельне перенесення, поворот навколо фіксованої точки, осьова симетрія.Т. Нех. на площ. Зад. 2 ортонорм. реперів 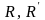. Тоді існує єдиний рух 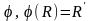.Дов.1). Існування. Спів ставимо кожній т. в репері 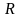т. в репері і покажемо, що відображення 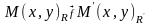задов. умовам теореми.а) 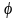-рух. Розгл. 2 точ. 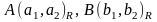тоді .Образи цих точок матимуть такі ж координати в репері 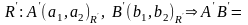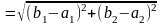. В рез. маємо . Отже, -рух. б) 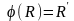.Нех. 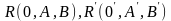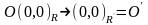.Т. . т. , т. 2). Єдність. Прип, що існує 2 різ. рухи 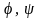, такі що 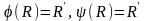. За припущ. 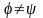, отже існує т. , для якої . Познач. 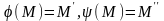.Позн. 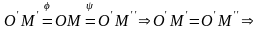репери .Маємо т. належить серединному перпендикуляру до 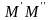.Аналогічно 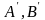належ. Тому самому серед перпендик.Отже, 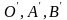леж. На 1 пр., що суперечить озн. Репера.

Рух І роду: ІІ роду: Рухи утворюють групу т.я

9. Група перетворень подібності. Гомотетія.

О: Перетворенням подібності з коефіцієнтом 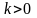наз. таке перетвор. Площини, при якому усі відстані змінюються в к разів. Тобто для точок А,В і їх образів А^/, В^/ рівність .

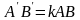О: Гомотетією з центром в точці 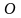і коеф. 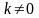наз. таке перетвор. Площини, при якому для б-якої т.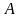 та її образа 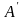вик. рівність .

Т: Гомотетія є перетворенням подібності. Дов. Нех. -гомотетія з центром в т. і коеф. .Розгл. дов. Точ. 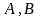та їх образи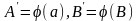 .За озн. 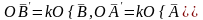.Віднявши ці рівності одерж. 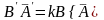.З ост. Рів. 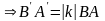.Отже -є перетвор. Подібності з коеф. .

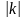Теорема: Нехай f – перетворення подібності з коеф к, g – гомотетія з центром в деякій т О і коеф к. тоді існує і до того ж єдиний рух h, що f=hg. Дов. Нехай g^-1 – гомотетія з центром в т.О і коеф 1\к тоді g*g ^-1= g ^-1*g=е. розглянемо перетворення fg^-1 і покажемо, що воно задовольняє умовам теореми.

1. це перетворення є рухом так як спочатку відстані змінюються в 1\к , а потім – в к разів, тобто не змінюються.

2. (f g ^-1) g = f (g ^-1*g) =fе=f

Припустимо, що існує 2 рухи h₁ h₂ такі, що f= h₁g, f= h₂g. h₁g= h₂g. (h₁g)g ^-1 =(h₂g) g ^-1. h1(gg ^-1 )=h₂ (g g ^-1). h₁e= h₂e. h₁= h₂ . доведено.

10. Група афінних перетворень. Задання афінних перетворень.

О: Афінним перетворенням площини наз. Таке перетвор. При якому б-які точки 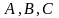, що леж на одній прямій відображаються в точ. , які теж леж. На одній пр. і при цьому зберіг. Їх просте відношення, тт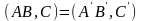 .Т: Нех. на площ. Зафіксовано 2 афінні репери 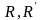.Тоді існує єдине аф. Перетвор. .Дов. 1) існування. Визначимо перетвор. площини наступ. способом.В т. 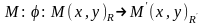.Покажемо, задов умові теореми.: А). - афінне. Розгл. т , що леж на , причому 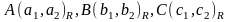. Тоді колінеарні, тт. 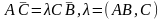.В репері 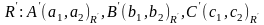З одержаних рівностей випливає 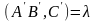.Б)Покажемо, що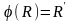 . Т. -старий початок перейде в новий. , 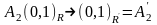.2)Єдиність.Нех 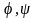-2 афін. Перетвор, які відобр.в .Прип. тт. існує т. і покаж, що це неможливо. Розгул. можливе розташ. т. відносно репера . За озн. а)Образи точ, які леж на 1 пр, теж леж на 1 пр., тому .Крім того 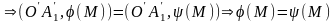Отже т. 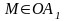Більш того на прямій 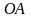та збігаються. б) Аналогічно розглянем випадок коли т. 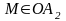в) проведемо через т. яка не належить корд. вісям пряму , яка перетинає вісі у т. 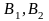Тоді за п. а),б): 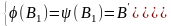Аналіт задання(ф-ли). 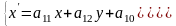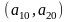де –поч. корд. інші корд базисних векторів

Композицією афінних перетворень є теж афінне перетворення. Отже, афінне перетворення утворює групу. Основними підгрупами цієї групи є:група рухів, група перетворень, афінні перетворення І роду.