30. Аналог алгебраїчного критерію стійкості Гурвіца для дискретних систем.

Алгебраїчні критерїї стійкості. Ці критерії було розроблечо стосов-но безперервних систем. Вони дозволяють визначити, чи всі корені ха­рактеристичного рівняння знаходяться в лівій напівплощині комплексно'! площини коренів. Застосувати ці критерії безпосередньо для дослідження імпульсних систем неможливо. Дійсно, характери-стичне рівняння імпульсної системи можна подати у вигляді

або

Для рівняння (10. 70) умовою стійкості є розміщення всіх коренів всередині кола одиничного радіуса в площині коренів z, а не в лівій напівплощині. Для рівняння (10. 71) умовою стійкості залишається розміщення всіх коренів р, в лівій напівплощині коренів р. Проте кри-терії стійкості застосовуються лише до характеристичних рівнянь у вигляді поліномів, а рівняння (10. 71) є трансцендентним. Щоб застосу­вати відомі алгебраїчні критерії стійкості безперервних систем для дослідження імпульсних систем, необхідно виконати w-перетворення, яке полягає в заміні комплексної змінної z в рівнянні (10. 70) на комплексну змінну w за допомогою формули Внаслідок цього перетворення утворюється поліноміальне рівняння

(10. 72)

Зоною стійкості для його коренів буде ліва напівплощина коренів w (рис. 10. 12, в). До цього рівняння можна застосувати всі алгебраїчні критерії стійкості — Вишнєградського, Гурвіца і Рауса, тому що умова стійкості для рівняння (10. 72) збігається з умовами стійкості безперер-вних систем.

Наприклад, для використання критерію Гурвіца необхідно визначи-ти передаточну функцію замкнутої системи і записати характеристичне рівняння Потім у цьому рівнянні треба виконати підстановку

Після приведения цього виразу до загального знаменника дістанемо нове характеристичне рівняння того самого порядку

де а'. — коефіцієнти, що є комбінаціями доданків і сум коефіцієнтів а,

Згідно з критерієм Гурвіца для стійкості імпульсної системи не-обхідно і достатньо, щоб при визначник Гурвіца і всі його діагональні мінори були додатними:

Приклад 10. 6. Визначити за критерієм Гурвіца стійкість системи, характеристичне рівняння якої мае вигляд

31. Аналог частотного критерію стійкості Найквіста для дискретних сау.

Аналог критерію Найквіста. Подібно до безперервних систем для дослідження стійкості замкнутих імпульсних систем можна використо-вувати АФХ розімкнутих систем.

Аналог критерію Найквіста стосовно імпульсних систем форму-люеться так:

1) якщо система стійка в розімкнутому стані або нейтральна, тобто мае нульові полюси pt, то для стійкості замкнутої Системи необхідно і достатньо, щоб_АФХ розімкнутої системи при змінюванні відносної частоти и> від 0 до п не охоплювала точку з координатами (-1, j0) і не проходила через неї;

2) якщо система нестійка в розімкнутому стані, то для стійкості замкнутої системи необхідно і достатньо, щоб АФХ розімкнутої системи при змінюванні частоти ш від 0 до л охоплю­ вала точку з координатами (-1, j0) к/2 разів, де к — кількість коренів характеристичного рівняння безперервної частини розімкнутої системи, що мають додатну дійсну частину, або, що те саме, кількість коренів zi характеристичного рівняння ро-зімкнутої імпульсної системи, модулі яких більші за одиницю.

Отже, під час дослідження стійкості за критерієм Найквіста передусім треба перевірити стійкість розімкнутої системи і, якщо вона нестійка, визначити кількість коренів р. з додатною дійсною частиною. Це зробити неважко, якщо мати на увазі, що основні полюси передаточних функцій безперервної W{p) та імпульсної W*(p) розімкнутих систем збігаються, тоб­то робити висновок про стійкість розімкнутої імпульсної системи можна на підставі перевірки стійкості її безперервної частини.

АФХ розімкнутої стійкої імпульсної системи, що відповідають стійкій (крива I) і нестійкій (крива 2) замкнутим імпульсним системам,

зображено на рис. 10. 14, а. На рис. 10. 14, б наведено АФХ розімкнутих систем, стійкої (крива 1) і нестійкої (крива 2 ) в замкнутому стані при к = 2.

Як бачимо, формулювання критерію Найквіста для імпульсних систем залишаеться таким самим, як і для безперервних. Відмінність полягае в тому, що АФХ імпульсних систем при w = Пи закінчуються на дійсній осі, а не стягуються в початок координат.

Другою особливістю є залежність АФХ імпульсної системи від періоду квантування Т₀ імпульсного елемента. Це неважко виявити, як-що проаналізувати побудову АФХ імпульсної системи за АФХ безпе-рервної системи (див. рис. 10. 11, б).

Введения імпульсного елемента в деяких випадках може бути засобом стабілізації нестійких замкнутих безперервних систем. рекомендуеться період квантування вибирати з умови

де су — частота, при якій АФХ безперервної частини розімкнутої сис­теми перетинає додатну уявну піввісь.

Відповідно до критерію Найквіста стійкість замкнуто! системи мож-на визначати не тільки за АФХ розімкнутої системи, але й за логарифмічними характеристиками — амплітудною L (Я) і фазовою <р (Я). Для цього попередньо треба виконати w-перетворення і перейти до псевдочастоти (лямбда), застосувавши підстановку

Стосовно логарифмічних характеристик критерій Найквіста формулюеться так:

1) якщо система стійка або нейтральна в розімкнутому стані, то для стійкості замкнутої системи необхідно і достатньо, щоб на частоті зрізу λ_з, що відповідає L(λ) = О, фаза за модулем була менша π;

2) якщо система нестійка в розімкнутому стані і характеристичне рівняння мае к коренів z, модулі яких перевищують одиницю, то для стійкості замкнутої системи необхідно і достатньо, щоб при L(X) > 0 кількість перетинів фазовою характеристикою рівня -л зни-зу вгору була в А/2 разів більшою кількості перетинів у протилеж-ному напрямку.

Приклад 10. 7. Виконати дослідження стійкості замкнуто! імпульсної САК за допо-могою логарифмічних характеристик і визначити запаси стійкості no фазі й амплітуді, якщо передаточна функція системи в розімкнутому стані мае вигляд

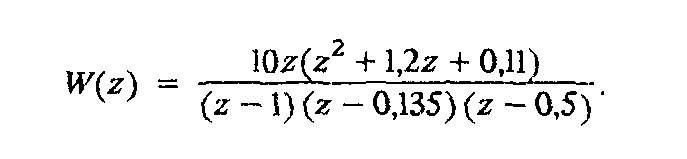
Розв'язання. Полюси передаточної функціі розімкнутої сисіеми z_{ — 1; z₂ — -0,135; г_ъ - 0,5, тому розімкнута система нейтральна і для дослідження стійкості замк-

нутої системи застосовується перше формулювання критерію Найквіста в логарифмічній формі.

Для побудови логарифмічних характеристик спочатку подамо чисельник переда-точної функції W(z) у вигляді добутку елементарних співмножників

а потім виконаємо w-перетворення, зробивши підстановку z - (1 + w)l<\ — w). Після спро-щень дістанемо

Подамо передаточну функцію W(w) у вигляді, зручному для побудови лога-рифмічних характеристик:

Виконаємо підстановку w - Д

і побудуємо ЛАХ Ј(І) і ЛФХ ір(Х).

Методика побудови Ј(Я) така сама, як і методика побудови асимптотичних ЛАХ без-перервних систем^ Низькочастотна (початкова) частина ЛАХ проходить через точку з координатами dA") = 201g26,7 = 28,5дБ, Ig X = 0 з нахилом -20 дБ/дек, тому що пе-редаточна функція мае співмножник VjX. Логарифми частот сполуки:

Фазова характеристика розраховується за формулою

Побудовані ЛАХ І ЛФХ зображено на рис. 10. 15.

Система регулювання на псевдочастоті зрізу А_з = 5(lg J₃ = 0,7) мае запас стійкості по фазі AjP - 64 °. Запас стійкості по амплітуді AZ. - 11 дБ.