2. Последовательность шагов по доказательству корректности схем-алгоритмов программ

Пример.

Рассмотрим определение результата деления двух натуральных чисел А и В в виде пары чисел «частное» и «остаток», не используя операции умножения и деления.

Обозначим:

СН – частное;

АА – остаток;

А – делимое;

В – делитель.

Схема алгоритма деления приведена на Рис. 5 .3.

Представим алгоритм, приведённый на рис. 5.3, в форме, принятой при верификации программ (Рис. 5 .4).

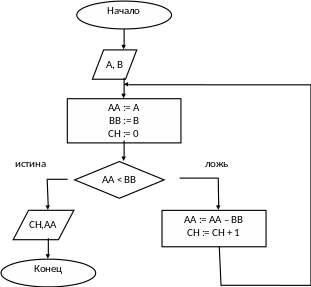
Рис. 5.3. Пример алгоритма деления натуральных чисел

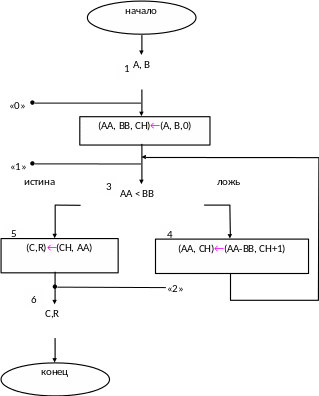
Рис. 5.4. Представление алгоритма в форме, принятой при верификации программ

Обычно при доказательстве правильности (корректности) операторы ввода вывода игнорируется.

Шаги по доказательству корректности программ выглядят следующим образом.

1. На схеме алгоритма выделяем точки разреза. Всегда будет нулевая точка лежащая на дуге исходящей из вершины “начало” и точки, на каждой дуге ведущей к вершине “конец” алгоритма. Кроме того, вводятся точки разреза как минимум на каждый цикл по одной точке.

2. На алгоритме выделяем множество путей, при этом путь должен обладать следующими свойствами:

1. путь должен начинаться и заканчиваться в точке разреза;

2. путь не должен содержать других точек разреза;

3. множество всех выделенных путей должно покрывать все ветви алгоритма, т.к. в данной схеме алгоритма 3 ветви, то выделяем 3 следующих пути:

α₀₁ = {«0», 2, «1»}

α₁₁ = {«1», 3, 4, «1»}

α₁₂ = {«1», 3, 5, «2»}

3. Формулируем предикаты, т.е. с каждой точкой разреза связывается предикат или некоторое индуктивное утверждение.

Назначение предиката состоит в том, чтобы описать соотношение между переменными в этой точке. Это индуктивное утверждение должно обладать тем свойством, что всякий раз, когда исполнение программы достигает данной точки, предикат должен быть истинным для текущих значений входящих в него переменных в данной точке.

Входной предикат связывается с начальной точкой разреза программы, а выходной с конечной точкой разреза.

Р₀: А, В – натуральные числа

Р₁: АА = А – СН * ВВ

Р₂: С = (A – R) / В

АА - это текущий остаток в цикле;

СН – текущее частное;

ВВ – делитель;

R – конечный остаток от деления.

Входное утверждение Р₀ (входной предикат) описывает все необходимые условия для нашего алгоритма. Выходное утверждение Р₂ (выходной предикат) описывает связь выхода с входом, т.е. ожидаемый результат. Предикат Р₁ вводится таким образом, чтобы он отражал основные свойства цикла.

4. Формулируем условия прохождения пути:

α_01: W₀₁ = истина

α_11: W₁₁ = AA ≥ BB

α_12: W₁₂ = AA < BB

5. Строим для каждого пути α_ij, ведущего из точки разреза i в точку j, некоторое верификационное условие

α_01: [P₀ ^ W₀₁]→[P₁] (5.1)

α_11: [P₁ ^ W₁₁]→[P₁] (5.2)

α_12: [P₁ ^ W₁₂]→[P₂]. (5.3)

Cуть метода заключается в демонстрации того, что из входного утверждения P₀ и преобразование выполняемого на данном пути следует утверждение, сформулированное в конце пути, например в точке “1” и так вплоть до выходного утверждения P₂

6. Доказательство корректности верификационных условий. Все три условия имеют вид p→q. Обычный метод доказательства таких утверждений сводится к тому, чтобы показать, что q истинно всякий раз, когда истинно Р, т.е. нужно доказать истинность q при условии истинности p.

Докажем истинность предложения (5.1) для пути α_01.

α_01: [(А, В: натуральные числа) ^ истина] → [АА = А – СН*ВВ]

P₁

Подставляем в предикат P₁ значения переменных после выполнения блока 2 схемы алгоритма (рис. 5.4).

А = А – 0 * В следовательно А = А (истинно)

Т.о. всё предложение истинно. Докажем истинность предложения (5.2) для пути α_11.

α_11: [(AA=A – CH*BB) ^ (AA ≥ BB)] → [AA = A – CH*BB] (5.4)

P₁ P₁

Чтобы доказать истинность предиката в конце пути (точка разреза «1»), достаточно доказать:

1. истинность P₁ при первом попадании в точку «1»;

2. истинность P₁(n+1) при условии, что справедливо P₁(n), где n – параметр цикла.

Т.о. необходимо доказать истинность предложения P₁(n) → P₁(n+1), т.е. при условии, что P₁(n) – истинно, доказать, что P₁(n+1) – истинно, и т.о. P₁(n) будет истинным для любого значения n.

Докажем истинность предиката P₁ при первом попадании в точку разреза «1», т.е. докажем истинность предложения (5.4).

AA – BB = A – (CH+1)*BB

AA – BB = A – CH*BB – BB

AA = A – CH*BB

Т.о. истинность предложения (5.4) на первой итерации доказана.

Пусть P₁ истинно на n-й итерации.

AA – n*BB = A – (CH+n)*BB

Докажем истинность на (n+1)-ой итерации:

AA – (n+1)*BB = A – (CH+n+1)*BB

AA – n*BB – BB = A – (CH+n)*BB – BB

AA – n*BB = A – (CH+n)*BB

Т.о. истинность на (n+1)-ой итерации доказана и т.о. предложение (5.4) истинно для любого n в рамках ограничений предложения (5.4).

Докажем истинность предложения (5.3) на пути α_12.

α_12: [(AA = A – CH*BB) ^ (AA < BB)] → [C = (A – R)/B]

P₁ P₂

Подставляем в предикат P₂ значения переменных после выполнения блока 5 схемы алгоритма (рис. 5.4).

CH = (A – AA)/B

AA = A – CH*B

Т.к. B ≡ BB (нигде не менялось), то получаем предикат P₁, истинность которого доказана.

AA = A – CH*BB

Поэтому предложение (5.3) истинно.

Данный подход позволяет обнаруживать ошибки. Например, внесём ошибку в блок 2 схемы алгоритма (рис. 5.4).

(AA, BB, CH) ← (A, B, 1)

Тогда α_01: [(A, B: натуральные числа) ^ истина] →

[AA = A – CH*BB]

A = A – 1*B

A ≠ A – B (ошибка).

Т.о. мы доказали, что схема алгоритма правильна по отношению к входному и выходному утверждению Р₀ и Р₂ , но то что программа не будет находиться в бесконечном цикле еще не доказано. Нет общего метода доказательства завершаемости программ, но обычно бывает достаточно неформальных рассуждений. В нашем случае алгоритм заканчивается только тогда когда AA < BB. Согласно входному утверждению Р₀, АА первоначально положительно и уменьшается при каждом повторении цикла на положительное число равное ВВ. Т.о. неформально установлено, что выполнение программы закончится.

Из анализа данного примера видно, что доказательство правильности весьма трудоемкий процесс и доказательство всегда длиннее самой программы