Потенциальное поле

Векторное поле называется потенциальным (или безвихревым или градиентным), если во всех точках поля ротор равен нулю,

Основные свойства потенциального поля:

1. Циркуляция потенциального поля по любому замкнутому контуру в этом поле равна нулю.

Для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости, равенство Ц=0 означает, что в потоке нет замкнутых струй, т.е. нет водоворотов. В потенциальном поле отсутствуют вихри.

2. В потенциальном поле криволинейный интеграл вдоль любой кривой L с началом в точке и концом в точке зависит только от положения точек и и не зависит от формы кривой.

3. Потенциальное поле является полем градиента некоторой скалярной функции U(x,y,z), т.е. если , то функция U(x,y,z) такая, что

Потенциальное поле определяется заданием одной скалярной функции

U=U(x,y,z) – его потенциал.

Потенциал векторного поля может быть найден по формуле

Пример: Установить потенциальность поля и найти его потенциал.

В качестве фиксированной точки (х₀, y₀, z₀) возьмем точку (0;0;0)

U(x,y,z)=

Примером потенциального поля является электрическое поле напряженности точечного заряда q.

Гармоническое поле

Векторное поле называется гармоническим, если оно одновременно является потенциальным и соленоидальным, т.е. если и .

Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.

Оператор Гамильтона.

Основными дифференциальными операциями (действиями) над скалярным полем U=U(x,y,z) и векторным полем являются , и . Действия взятия градиента, дивергенции и ротора называются векторными операциями первого порядка (в них участвуют только первые производные). Эти операции удобно записывать с помощью так называемого оператора Гамильтона (читается «набла»)

Этот символический вектор называется ещё оператором набла . Этот оператор приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями.

Умножение вектора на скалярную функцию U и вектор производится по обычным правилам векторной алгебры, а умножение символов на величины U, P, Q, R означает взятие соответствующей частной производной от этих величин.

Применяя оператор Гамильтона, получим дифференциальные операции первого порядка:

1. 

2. 

3. 

Векторные дифференциальные операции второго порядка.

После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка.

диф. операции 1-го порядка диф. операции 2-го порядка

U(M)		grad U(M)		div grad U(M)
				rot grad U(M)
		div		grad div
				div rot
		rot		rot rot

Существует пять дифференциальных операций второго порядка. Запишем некоторые формулы для дифференциальных операций 2-го порядка:

1. div grad U=

Наряду с оператором Гамильтона в векторном анализе и его приложениях используется оператор Лапласа, обозначаемый символом ∆. Оператор Лапласа определен следующей формулой - или .

Выражение для div grad U можно записать следующим образом

div grad U=

2. Применяя оператор Гамильтона легко получить , т.к. векторное произведение двух одинаковых векторов равно нулю. Это означает, что поле градиента есть безвихревое поле.

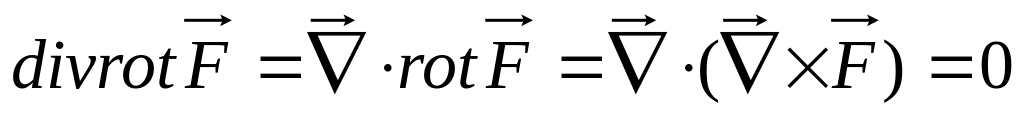3. , т.к. смешанное произведение трех векторов, из которых два одинаковые, равно нулю. Это означает, что поле вихря – соленоидальное, не имеет источников и стоков.