7. Звено связи

Звено связи между скоростью двигателя и углом поворота.

(2.22)

Применим преобразование Лапласа к (2.22):

(2.23)

Найдем передаточную функцию звена:

(2.24)

3. Составление структурной схемы и определение передаточной функции неизменяемой части системы

В соответствии с определёнными передаточными характеристиками звеньев и (рисунком 2.1) составим структурную схему системы:

Рисунок 3.1 – Структурная схема системы

Для упрощения схемы перенесем узел суммирования сигналов с выхода звена с передаточной функцией на его вход и с учетом равенства получим схему на рис. 4. Новая переменная на рис 4. Соответствует ошибке слежения, которая равна .

Рисунок 3.2 – Структурная схема системы

Определим передаточную функцию разомкнутой нескорректированной системы по управляющему воздействию, пологая, что и обратная связь разомкнута:

. (3.1)

Коэффициент усиления неизменяемой части системы равен:

(3.2)

При составлении уравнений динамики были приняты следующие допущения:

• все элементы системы не содержат существенных нелинейностей, поэтому могут быть описаны линейными уравнениями;

• момент инерции звена робота Jпостоянный;

• рассматривается режим холостого хода, то есть внешний момент нагрузки равен нулю;

• к.п.д. редуктора .

1. Определение коэффициента усиления усилителя мощности. Построение логарифмических частотных характеристик нескорректированной системы и определение устойчивости системы

Коэффициент усилителя мощности определяется на основе заданных параметров: максимальной амплитуды допустимой ошибки слежения , максимальной скорости слежения и максимального ускорения . На основе заданных параметров строится «запретная зона».

При синтезе следящих систем обычно неизвестен закон изменения входного сигнала и при определении условий работы систем оговаривают только максимальную скорость слежения и максимальное ускорение . В этом случае можно подобрать эквивалентный гармонический входной сигнал ₃ = _мах * sin (_кt). Найдем режим, при котором амплитуды скорости и ускорения эквивалентного сигнала равны максимальным заданным значениям. Для этого необходимо выполнение условий:

с^-1, (3.3)

град (3.4)

Введем понятие контрольной точки А_К с координатами:

, (3.5)

где – допустимое значение ошибки отработки входного сигнала.

дБ. (3.6)

По этим величинам можно построить контрольную точку А_К. С учетом ее в общем случае строится запретная область, в которую не должна заходить ЛАЧХ разомкнутой следящей системы. При этом слева от точки А_К строится прямая с наклоном –20 дБ/дек, а справа с наклоном –40 дБ/дек.

Если скорости и ускорения не превышают и , то при ЛАЧХ, расположенной выше запретной области, максимальная ошибка слежения не будет превышать _доп.

Рисунок 3.3 – График запретной зоны

Таким образом, ЛАЧХ скорректированной системы не должна заходить в запретную область, это условие необходимо учитывать при построении низкочастотной части характеристики.

Полагая, что коэффициент усилителя мощности равен единице, строится логарифмическая частотная характеристика неизменяемой части системы (L_H(ω, =1)) по передаточной функции , (рисунок 3.3). Чтобы максимальная допустимая ошибка не превышала заданную, необходимо поднять низкочастотную часть характеристики (L_H(ω, =1)) на 6 дБ выше запретной зоны.

Построив эту характеристику, находим необходимый коэффициент усиления неизменяемой части из рисунка 3.3.

дБ. (3.7)

дБ, дБ. (3.8)

дБ. (3.9)

дБ. (3.10)

Откуда .

Подставив в (3.2) значение определим общий коэффициент усиления:

. (3.11)

Передаточная функция незамкнутой системы имеет вид (3.1):

Рассмотрим передаточную функцию звена второго порядка:

.

Определим корни характеристического уравнения звена второго порядка:

(3.9)

Так как дискриминант:

то корни комплексные, следовательно, звено является колебательным и его

передаточную функцию можно записать в виде:

с (3.11)

(3.12)

Построение ЛАЧХ.

Определяем частоты сопряжения:

c^-1 (3.13)

c^-1 (3.14)

На оси абсцисс отметим сопрягающие частоты и через полученные точки проводим вертикальные прямые.

Найдем величину: L_К = 20 lg К₀+10=20 lg98.14+10=49.837дБ.

Строим точку «А» с координатами: ω=1, L_К=49.837дБ.

Через полученную точку «А» проводим прямую с наклоном –20 дБ/дек, так как передаточная функция содержит сомножитель p в знаменателе.

При пересечении с первой вертикальной прямой, соответствующей частоте сопряжения ω₁, наклон асимптотической характеристики изменяется на – 40 дБ, так как ω₁ соответствует звену второго порядка, находящемуся в знаменателе. Поэтому наклон характеристики на этом участке будет равен –60 дБ/дек. Правее частоты сопряжения ω₂ наклон изменится еще на –20 дБ и станет равным –80 дБ/дек.

Построенная характеристика нескорректированной системыL_Н(ω) приведена на рис. 3.3.

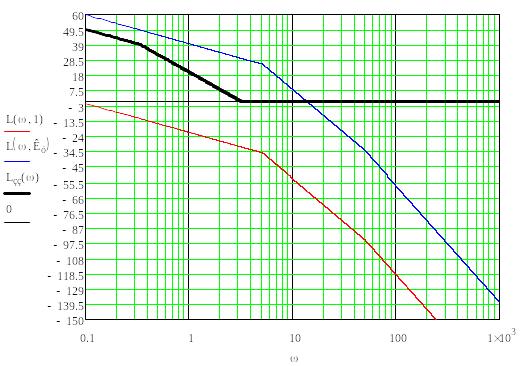
Рисунок 3.4 – ЛАЧХ неизменяемой части

Построение ЛФЧХ.

Определим устойчивость системы по ЛАЧХ.

Для этого построим ЛФЧХ и определим запас по фазе на частоте среза

ω_c=6.807с^-1.

Суммарная фазовая характеристика разомкнутой системы строится алгебраическим сложением ординат фазовых характеристик звеньев:

, (3.15)

где

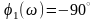(3.16)

(3.17)

(3.18)

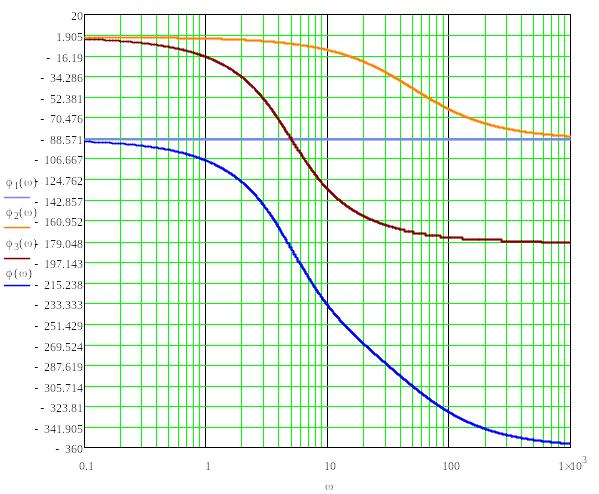
Рисунок 3.5 – ЛФЧХ неизменяемой части

Критерий устойчивости Найквиста, применительно к логарифмическим частотным характеристикам разомкнутой системы L(ω) иφ(ω), может быть сформулирован следующим образом:

замкнутая система автоматического регулирования устойчива, если разность между числами положительных и отрицательных переходов фазовой характеристики разомкнутой системы φ(ω) через линию φ = -180° в диапазоне частот, где L(ω)>0, равна q/2, где q– число корней с положительной вещественной частью характеристического уравнения разомкнутой системы.

Положительным переходом считается переход характеристикиφ(ω)снизу вверх через линию φ = -180°, а отрицательным сверху вниз.

Из рисунка 3.4 следует, что в диапазоне частот, в котором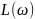 больше нуля, разность между числами положительных и отрицательных переходов 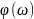через линию равна единице (имеется один отрицательный переход), то есть не равна нулю (q/2=0, где q - число корней с положительной вещественной частью характеристического уравнения разомкнутой системы). Следовательно, замкнутая система неустойчива.

Упрощенная формулировка критерия для случая q = 0.

Электромеханические системы, как правило, состоят из устойчивых звеньев, поэтому число корней с положительной вещественной частью

характеристического уравнения разомкнутой системы равно нулю. В этомслучае можно использовать упрощенную формулировку критерия.

Система в замкнутом состоянии устойчива, если на частоте срезаω_С ЛФЧХ разомкнутой системы проходит выше линии φ = – 180⁰. Частота срезаω_С - это значение частоты ω,при которой L (ω_С) = 0.

Определим корни характеристического уравнения звена второго порядка:

,

,

.

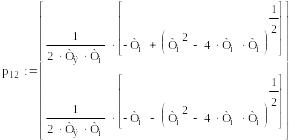
Так как число корней характеристического уравнения разомкнутой системы с положительной вещественной частью равно нулю(q=0), то можно использовать упрощенную формулировку критерия.

По логарифмической амплитудно-частотной характеристике разомкнутой системы L(ω) в точке пересечения характеристикой оси абсцисс определяем частоту среза ω_c=8.116 с^-1 (рис. 3.3).

Проводим вертикальную линию до пересечения с логарифмическойфазочастотной характеристикойφ(ω)и определяем значение фазы, которое равно -217°. Таким образом, на частоте среза фазочастотная характеристика расположена ниже линии φ = -180°.

Следовательно, система в замкнутом состоянии неустойчива.