Контрольные вопросы

1. Что такое сочетание из п различных элементов, содержащее элементов?

2. Какие два сочетания считаются различными?

3. Как определить максимальное число различных сочетаний из п различных элементов по т элементов в каждом?

4. Как определяется символ 0! ?

2.3. Размещения

Определение. Любой упорядоченный набор различных элементов, взятых из множества, состоящего из элементов, называется размещением.

Для каждого из сочетаний существует различных размещений. Следовательно, число размещений из элементов по составляет

. (1)

Пример. В соревновании участвуют 8 команд. Какое количество различных способов распределения первых трех мест существует?

Решение. .

Контрольные вопросы

1. Что такое размещение из различных элементов, содержащее элементов?

2. Какие два размещения считаются различными?

3. Как вычислить максимальное число различных раз­ме­щений из различных элементов по элементов в каждом?

2.4. Формула Стирлинга

Для приближенного вычисления факториала в случае больших значений аргумента используется формула Стирлинга⁵ [10]

. (1)

2.5. Формула бинома Ньютона

Примечательно, что числа сочетаний из элементов по являются коэффициентами в формуле бинома Ньютона [9]

. (1)

При этом так как , то

. (2)

§ 3. Геометрическое определение вероятности событий

Во многих случаях применение классического способа вычисления вероятности оказывается невозможным по причине бесконечного числа возможных исходов испытаний. Например, пусть в результате испытания внутри круга радиусом размещается точка (см. рис. 1). Предположим, что вероятность попадания точки в область Ц, составляющую часть круга, не зависит от формы и положения этой области, а зависит только от ее площади. Тогда естественно определить вероятность попадания точки в область Ц как

, (1)

где - площадь области Ц.

Рис. 1. Геометрический способ вычисления вероятности

Аналогичная ситуация возникает в задаче о встрече. Два человека договорились встретиться в определенном месте между 12 часами и часом. Человек, пришедший первым, ждет другого 20 минут и уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанного часа происходит случайно и моменты прихода независимы.

Решение

Пусть - время прихода лица , - время прихода лица . Встреча состоится, если

. (2)

Представим задачу графически в Декартовой системе координат, в которой по оси Х отложим время х прихода лица А, а по оси Y – время y прихода лица В (рис. 2).

Приход лиц и в назначенное место встречи описывается случайной точкой в квадрате на указанной плоскости со стороной 60 мин. Событие "встреча" соответствует попаданию точки в область, определяемую неравенством (2). Более подробно это неравенство можно записать в виде:

если , то

или

если , то .

Эта область на рисунке заштрихована.

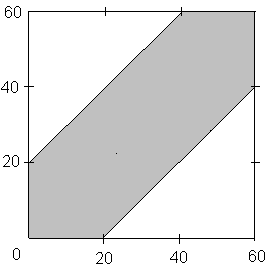
Рис. 2. Геометрический способ вычисления вероятности в задаче о встрече

Вероятность встречи можно вычислить как отношение площади заштрихованной области к площади квадрата, т.е.

.

Приведенные примеры можно использовать при решении задач, в которых целесообразно применение геометрического способа вычисления вероятности.