- •Тема 12.1. Теория вероятностей
- •1. Случайные события
- •1.1. Классификация событий
- •1.2. Алгебра событий. Диаграммы Эйлера-Венна1
- •Сумма и произведение любого числа событий.
- •Виды событий и их множеств, свойства операций над событиями
- •Свойства основных операций над событиями
- •Контрольные вопросы
- •2. Вычисление вероятностей
- •2.1. Классическое определение вероятности событий
- •1.1. Классическая схема испытаний
- •1.2. Свойства функции вероятности, определенной по классической схеме
- •Контрольные вопросы
- •2. Элементы комбинаторики
- •2.1. Перестановки
- •Контрольные вопросы
- •2.2. Сочетания
- •Теорема
- •Контрольные вопросы
- •2.3. Размещения
- •Контрольные вопросы
- •§ 4. Аксиоматическое определение вероятности событий
- •4.1. Аксиоматическое построение теории вероятностей
- •4.2. Свойства функции вероятности
- •Пример.
- •Контрольные вопросы
- •§ 5. Статистическое определение вероятности событий
- •Контрольные вопросы
Тема 12.1. Теория вероятностей
Пример. 27
1. Случайные события
Предметом теории вероятностей являются процессы, на протекание которых оказывают влияние не только контролируемые, но и неконтролируемые факторы. В силу этого традиционный детерминистический подход оказывается невозможным. Теория вероятностей исследует те процессы, которые в принципе могут быть воспроизведены неограниченное количество раз при одинаковом наборе условий их воспроизведения и характеризующиеся свойством повторяемости результатов их осуществления.
Вероятность является следствием неисчерпаемости природы вглубь и вширь. Не все можно точно знать.
1.1. Классификация событий
Событие
это то, что может произойти или нет при
выполнении определенного комплекса
условий
или как говорят при проведении испытания.
Среди возможных событий выделяют
достоверные
и невозможные.
Если при каждом испытании всегда
происходит некоторое событие, то оно
называется достоверным.
Для обозначения достоверного события
будет использоваться символ
![]() .
Если при испытании некоторое событие
заведомо не может произойти, то оно
называется невозможным.
Невозможное событие обозначается
символом
.
Если при испытании некоторое событие
заведомо не может произойти, то оно
называется невозможным.
Невозможное событие обозначается
символом
![]() .
.
Если
событие
![]() не является достоверным или невозможным,
то оно часто называется случайным.
не является достоверным или невозможным,
то оно часто называется случайным.
Понятие испытания в теории вероятности является одним из основных понятий. Оно несколько отличается от понятия испытания или эксперимента в физике или химии.
Часто
при проведении физического испытания
не все его возможные исходы заранее
известны. В отличие от этого теория
вероятностей предполагает, что известен
перечень всевозможных исходов испытания.
Обычно считается также, что испытание
может быть воспроизведено любое
количество раз. При этом события
характеризуются повторяемостью частоты
их появления при многократных испытаниях.
В этом случае используется количественная
оценка возможности появления событий.
Она осуществляется посредством
вероятности
![]() ,
которая отражает соотношение контролируемых
и неконтролируемых факторов, оказывающих
влияние на результаты испытания.
,
которая отражает соотношение контролируемых
и неконтролируемых факторов, оказывающих
влияние на результаты испытания.
Прежде чем перейти к изучению способов определения вероятности, остановимся более подробно на операциях над событиями.
1.2. Алгебра событий. Диаграммы Эйлера-Венна1
Обычно события обозначаются прописными буквами латинского алфавита. Некоторые из событий оказываются связанными друг с другом. Эта связь выражается отношениями включения и равносильности событий.
Отношение включения события в событие
 .
.
Пусть
из того, что произошло событие
,
следует, что произошло также событие
.
В этом случае говорят, что
влечет за собой
,
или
является частным случаем
,
или
включено в
.
Это обстоятельство обозначают символом
![]()
![]() или
или
![]() . (1)
. (1)
Отношение "влечет" является отношением порядка на множестве событий. Это означает, что
![]() (2)
(2)
Первое из выражений (2) называют свойством рефлексивности операции включения, а второе – свойством транзитивности.
Отношение равносильности событий и .
Если
событие
влечет за собой событие
(![]() )
и если событие
влечет за собой событие
(
)
и если событие
влечет за собой событие
(![]() ),
то говорят, что
и
равносильны.
Это записывают
),
то говорят, что
и
равносильны.
Это записывают
![]() . (3)
. (3)
Иначе говоря, эти события или наступают или не наступают вместе. Поэтому их можно рассматривать как эквивалентные и не отличать одно от другого.
Одни события могут использоваться для формирования других событий с применением некоторых операций. Совокупность таких операций и их свойства называют алгеброй событий. К этим операциям относят следующие.
Произведение (пересечение) событий.
Событие, состоящее в наступлении обоих событий и , называют произведением (пересечением) событий и . Его обозначают
![]() .
.
Сумма (объединение) событий.
Событие, состоящее в наступлении или события или события , или обоих событий вместе называют суммой (объединением) событий и . Его обозначают
![]() .
.
Унарная (выполняется над одним операндом) операция формирования противоположного события.
Событие
![]() состоит в том, что событие
не произошло. Два события
и
называют противоположными.
Для них, очевидно, одновременно выполняются
следующие соотношения
состоит в том, что событие
не произошло. Два события
и
называют противоположными.
Для них, очевидно, одновременно выполняются
следующие соотношения
![]() , (4)
, (4)
где - достоверное событие,
- невозможное событие.
Разность двух событий.
Событие, состоящее в том, что событие произошло, а событие не произошло, называется разностью событий и . Его обозначается
![]() или
или
![]() .
.
Графическая интерпретация перечисленных отношений и операций над событиями осуществляется диаграммами Эйлера-Венна [1], [18]. Они представлены на рис. 1-5.
В
А |
А
В
|
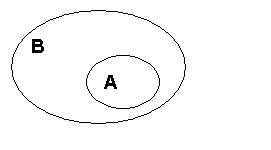
Рис. 1. Иллюстрация отношения включения события А в В (А В) |
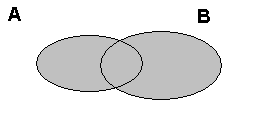
Рис. 2. Иллюстрация операции умножения событий А и В (А В) |
|
|
А
В
|
А
|
Рис. 3. Иллюстрация операции сложения событий А и В (А + В) |
Рис.
4. Иллюстрация операции взятия
противоположного
события А
|
|
В |
А |
|
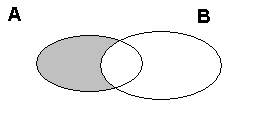
Рис. 5. Иллюстрация разности событий А и В (А – В) |
|
Операции сложения и умножения событий легко обобщаются на случай, когда число операндов больше двух.