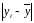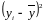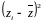Задача 1. Вычисление показателей вариации

Вычислите показатели вариации по каждой из выборок X, Y, Z:

• среднее арифметическое;

• моду;

• медиану;

• размах вариации;

• дисперсию;

• стандартное отклонение;

• среднее линейное отклонение;

• коэффициент вариации.

Решение:

Среднее значение ‑ средняя арифметическая простая:

где n ‑ объем выборки.

.

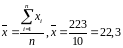
Например, если объем исследуемой совокупности n = 20, то номер медианы

Тогда медианой будет среднее из двух значений признака, стоящих в упорядоченном ряду под номерами 10 и 11:

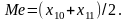
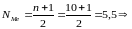
_{Размах вариации} ‑ разность между максимальным и минимальным значениями признака в совокупности:

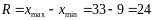
_Среднее линейное отклонение:

Среднее квадратическое отклонение ( ) представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней.

_{Формула расчета следующая:}

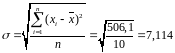
Квадрат среднего квадратического отклонения называется дисперсией (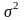 ). Дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, для проверки статистических гипотез.

Она вычисляется по формуле

:

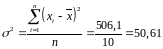
_{Аналогично рассчитаем показатели для выборок y и z:}

Найдем среднее значение по У:

Мода по У:

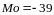
_{Медиана по У:}

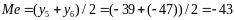
_{Размах вариации} ‑ разность между максимальным и минимальным значениями признака в совокупности:

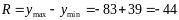
_Среднее линейное отклонение по У:

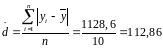
_{Среднее} квадратическое отклонение по У:

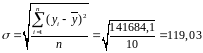
_{Дисперсия по У:}

Коэффициент вариации:

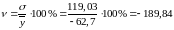
_{Расчет показателей вариации.}

_Табл.3

№
1	-83	145,7	21228,49
2	-82	144,7	20938,09
3	-77	139,7	19516,09
4	-72	9,3	86,49
5	-68	130,7	17082,49
6	-61	123,7	15301,69
7	-59	121,7	14810,89
8	-47	109,7	12034,09
9	-39	101,7	10342,89
10	-39	101,7	10342,89
	-627	1128,6	141684,1

Найдем среднее значение по Z :

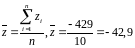
_{Медиана по Z:}

_{Размах вариации}

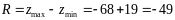
_{Среднее} квадратическое отклонение по Z:

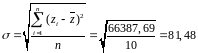
_{Дисперсия по Z:}

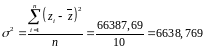
_Среднее линейное отклонение по Z:

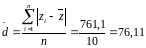
Коэффициент вариации:

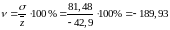
_{Расчет показателей вариации.}

_Табл.4

№
1	-83	27,9	778,41
2	-75	19,9	396,01
3	-67	11,9	141,61
4	-63	7,9	62,41
5	-62	6,9	47,61
6	-57	1,9	3,61
7	-51	4,1	16,81
8	-46	9,1	82,81
9	-33	22,1	488,41
10	-14	41,1	1689,21
	-551	152,8	3706,9