Еквівалентність множини. Потужність множини. Порівняння потужностей.
Озн.Множина наз.скінченною, якщо кількість її елементів визначається певним натуральним числом. В іншому випадку множина – нескінченна.
Нехай
,
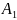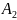– скінченні множини, порівняємо їх за
кількістю елементів.
І-й спосіб: перерахунок
Множина
-
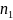елементів,
-
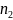елементів,для 2-ох натуральних чисел
та
має місце одне і лише одне із співвідношень:
Або
=
або
або
А |
а |
б |
в |
г |
В |
𝛼 |
𝛽 |
𝛾 |
𝛿 |
А – множина укр.літер
В – латинські
Зауважимо,що першим способом можна порівнювати лише скінченні множини, а 2-м – нескінченні.
-
N
1
2
…
n
M
…
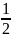
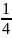
Нехай А, В – множ.елем. Якщо кожному елементу А за деяким правилом чи законом поставити у відповідність один і лише один елемент множини В, при цьому кожен елемент множини В відповідатиме єдиному елементу множини А, то говорять, що між множинами А і В встановлено взаємно однозначну відповідність. Так між множинами встановлено взаємно однозначну відповідність. Так між множинами M,N встановлено взаємо однозначну відповідність(n<=> ).Дві множини А і В назив. Еквівалентними, якщо між їх елементами можна встановити взаємооднозначну відповідність. Позначають А~ В. Відношення еквівалентності має такі властивості, що випливають із означення:1) А~ А – рефлективність; 2)А~ В тоді В~ А – симетричність;3) А~ В і В~ С тоді А~ С – транзитивність. Приклади: еквівалентними між собою є множини точок концентричних кіл та множини паралельних сторін паралелограма.
Потужність множини. Нехай А – множина елементів довільної природи. Розглянемо всі множини,які еквівалентні множині А. За властивістю транзитивності всі вони будуть еквівалентними між собою. А~ В і В~ С тоді А~ С. Назвемо таку сукупність множин класом еквівалентних множин. Таким способом розіб’ємо всі множини на класи: 2 –і множини попадають в один клас лише тоді,коли вони еквівалентні між собою.Очевидно,що скінченні множини утворять класи:2 елем.і так даліелем.множин. Подібна ситуація і з нескінченними множинами, бо не всі нескінченні множини між собою еквівалентні,вони теж розіб’ються на класи. Кожному класу еквівалентних множин поставимо у відповідність символ,наприклад μ, який називатимемо потужністю множин даного класу кожної з множин класу. Позначають А(подвійна риска над літерою А)=μ(потужність множини А дорівнює μ). Для скінченних множин,потужність дорівнює кількості елементів у множині. Для нескінченних множин потужність називають ще кардинальним числом.
Порівняння
потужностей.І)
Нехай А
і В
– скінченні, множина А
-
елемент,множина В
-
елемент.
Можливо одне і лише одне із 1)
=
2)
<
3)
>
.
Використовуючи поняття еквівалентності
робимо висновки,що 1)
=
тоді і тільки тоді, коли А~
В
тоді
(А=В);
2)
<
<=>,
коли А~
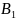⊂В;
3)
>
<=>,коли
В~
⊂А.ІІ)А
і В
– нескінченні:1)
А~ В;2) А~
⊂В;3)
В~
⊂А;
4) А~
⊂В
і В~
⊂А.
Теорема еквівалентності(Кантора-Берштейна). Якщо кожна з 2-х множин містить правильну підмножину, еквівалентну 2-ій множині, то ці множини еквівалентні. Отже, у 4-ому випадку А=В(над А і В ставити = і далі у висновку).Висновок:Для 2-ох множин А і В, як скінченних так і нескінченних має місце одне і лише одне співвідношення мі потужностями:1) А=В;2) А<В;3)А>В. Можна показати,що крім випадків 1- 4 інших бути не може. Існування потужності вищої від даної. Нехай множина А-скінченна,приєднання до множини одного або кількох елементів збільшує її потужність,навіть може стати нескінченною. Для нескінченних множин ситуація інша.Теорема:Потужність будь – якої множини менша за потужність всіх її підмножин.