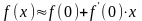- •1 . Матриці, основні поняття
- •2 ) Різновиди рівняння площини у просторі:за трьома точками, у відрізках на осях, нормальне.
- •2)Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння площини і його дослідження.
- •4)З означення диференціала функції випливає, що при достатньо малих і має місце наближена рівність
- •5) Диференціальні рівняння першого порядку. Основні поняття.
- •1) Визначники квадратних матриць. Способи обчислення визначників.
- •2) Кут між площинами. Умови паралельності і перпендикулярності двох площин.
- •4) Обчислення наближеного значення функції в точці за допомогою повного диференціала.
- •5) Диференціальні рівняння з відокремлюваннями змінними.
- •1)Визначник -го порядку. Теорема Лапласа
- •2) . Різновиди рівняння прямої в просторі: канонічне, параметричні, за двома точками.
- •3) Похідні вищих порядків.
- •4) Знаходження екстремуму функції кількох змінних
- •3/Застосування правила Лопіталя у невизначеностях виду ; ; ; .
- •4. Невизначений інтеграл та його властивості.
- •5. Диференціальні рівняння другого порядку, що допускають пониження порядку
- •1. Основні поняття системи n лінійних алгебраїчних рівнянь з n змінними. Правило Крамера
- •2.Парабола: означення, рівняння, графік
- •3. Необхідна і достатня ознаки зростання (спадання) функції
- •4.Метод безпосереднього інтегрування невизначених інтегралів
- •5. Рівняння Бернуллі.
- •Перший спосіб
- •Другий спосіб
- •3. . Екстремум ф-ції, необхідна та достатня умови існування екстремуму.
- •5.Лінійними неоднорідними диф. Рівняннями 2го порядку зі сталими коефіцієнтами
- •1,Система лінійних алгебраїчних рівнянь (слар) — в лінійній алгебрі це система лінійних рівнянь виду:
- •2,Поняття границі функції
- •3, Необхідною умовою існування екстремуму в точці диференційовної функції є рівність нулю її похідної: .
- •4.Інтегрування функцій, які містять у знаменнику квадратний тричлен.
- •5. Поняття ряду. Збіжність ряду та його сума.
- •1.Основні поняття слар. Системи лінійних однорідних рівнянь.
- •4.Метод невизначених коефіцієнтів.
- •5.Властивості збіжних рядів.
- •1.Скалярний і векторний добуток. Властивості векторного добутку.
- •2.Теорема про зв'язок між нескінченно малими і нескінченно великими функціями.
- •3.Функції двох змінних. Область визначення.
- •4.Інтегрування функцій, що містять ірраціональності.
- •5.Необхідна ознака збіжності ряду.
- •5. Питання
- •2)Якщо в деякому околі точки Хо,крім можливо самой точки Хо, виконується нерівність 0 і кожна з ф-цій та має границю в точці Хо, то .
- •3) Нехай в деякому околі точки Хо,крім можливо самой точки Хо, виконується нерівність
- •1) ,2) ,3) , Якщо .
- •4. Визначений інтеграл та його властивості.
- •5. Радикальна ознака Коші.
- •1. Записати рівняння прямої, яка проходить через точку з кутовим коефіцієнтом .
- •2. Неперервність функції в точці: Застосування поняття неперервності при обчисленні границь функцій.
- •3. Градієнт функції .
- •4. Формула Ньютона-Лейбніца для обчислення визначених інтегралів.
- •5. Інтегральна ознака Коші.
- •22. 1. Кут між двома прямими заданими канонічним рівнянням. Умови паралельності і перпендикулярності прямих.
- •2. Властивості функцій, неперервних у точці.
- •23. 1. Рівняння прямої з кутовим коефіцієнтом.
- •2. Властивості функцій, неперервних на відрізку.
- •1. Матриці основні поняття. Різновиди матриць.
- •Задачі, які приводять до поняття похідної: задача про продуктивність праці, задача про кутовий коефіцієнт дотичної.
- •Загальна схема побудови графіка функції за допомогою похідної.
- •Застосування визначеного інтеграла до обчислення площ фігур, обмежених лініями.
- •5. Степеневі ряди. Основні поняття. Теорема Абеля.
- •Дії над матрицями. Властивості дій над матрицями.
- •Означення похідної. Диференційовність та неперервність функції в точці і на проміжку.
- •5. Радіус, інтервал, область збіжності ряду.
- •Визначники квадратних матриць. Способи обчислення визначників.
- •Правила диференціювання сталої, суми, добутку, частки функцій, та наслідки з них.
- •Екстремум функції, необхідна та достатня умови існування екстремуму.
- •5. Ряд Тейлора.
- •Визначник -го порядку. Теорема Лапласа.
- •2.Геометричний зміст похідної. Рівняння дотичної. Поняття нормалі до графіка функції та її рівняння. Економічний зміст похідної.
- •3) Економічний зміст похідної: похідні V(X), d(X), p(X) дорівнюють маргінальній вартості, доходу та прибутку, відповідно.
- •3.Градієнт — це вектор з координатами , який характеризує напрям максимального зростання функції z - f(X,y) у точці р0 (х0, у0):
- •4.Невласний інтеграл іі роду.
- •5.Використання рядів до наближених обчислень функцій. Алгоритм наближеного обчислення функції f (X) в точці х0
- •1.Мінори та алгебраїчні доповнення елементів.
- •2.Похідна складної та оберненої функцій.
- •3.Частинні похідні вищих порядків. Теорема про рівність мішаних похідних.
- •4.Застосування визначеного інтеграла до обчислення площ фігур, обмежених лініями
1) ,2) ,3) , Якщо .
Якщо
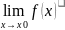 існує
то для довільного натурального m
існує
то для довільного натурального m
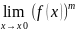 =
=
Питання 3 . Повний приріст і повний диференціал функції двох змінних.
 Нехай
маємо функцію двох змінних z
= f
(x;y).
Якщо х та у мають одночасно приріст Δх
та Δу, то різницю f
(x+Δx;
y+Δу)
– f(x;y)
називають повним приростом функції і
позначають Δz
= f
(x+Δx;
y+Δу)
– f(x;y)
Нехай
маємо функцію двох змінних z
= f
(x;y).
Якщо х та у мають одночасно приріст Δх
та Δу, то різницю f
(x+Δx;
y+Δу)
– f(x;y)
називають повним приростом функції і
позначають Δz
= f
(x+Δx;
y+Δу)
– f(x;y)
Головна лінійна відносно Δх та Δу частина повного приросту функції називається повним диференціалом:
dz = f´x(x,y) Δх + f´y(x,y) Δу
Питання 4 Інтегрування найпростіших раціональних дробів.
Інтеграли від найпростіших раціональних дробів І-го та П-го типів знаходять методом безпосереднього інтегрування. При інтегруванні найпростішого дробу Ш-го типу треба спочат-ку в знаменнику виділити повний квадрат, а потім той вираз, що під квадратом, замінити через нову змінну. Інтеграл від найпростішого дробу типу IV шляхом повторного інтегрування частинами зводять до інтеграла від найпростішого дро-бу типуIII.
Питання 5 . Гранична ознака порівняння.
Якщо
задано два ряди з додатними членами
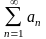 і
і
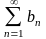 ,
причому існує скінченна границя
,
причому існує скінченна границя
 То
ряди одночасно є або збіжними, або
розбіжними.
То
ряди одночасно є або збіжними, або
розбіжними.
19 БІЛЕТ
1. Вивести рівняння прямої, що проходить через дві точки і рівняння прямої у відрізках на осях.
Рівняння прямої,що проходить через дві точки
Відомі
координати двох точок на прямій
L:
М
(x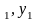 )
та М
)
та М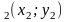 .
.
М
М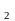 (х
(х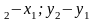 )
)

Рівняння прямої у відрізках на осях
Відомо,що пряма L відсікає на осях координат відрізки довжиною а і в
Точки
перетину прямої L
з
осями координат: М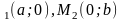
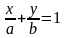 де
а – довжина відрізка на осі ОХ , а в- ОУ.
де
а – довжина відрізка на осі ОХ , а в- ОУ.
2.
Розкриття невизначеностей вигляду
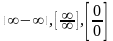 при
застосуванні ірраціональних функцій
та многочленів під час обчислення
границь функцій.
при
застосуванні ірраціональних функцій
та многочленів під час обчислення
границь функцій.
1)
Невизначеність
виду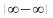 :
:
а)
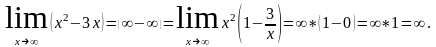
б)
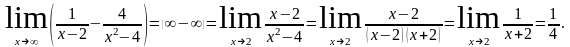
Для функцій, які мають границю на нескінченності, залишаються справедливі всі сформульовані теореми.
2)
Невизначеність
виду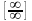 ,задана
відношенням двох многочленів:
,задана
відношенням двох многочленів:

Поділимо
чисельник і знаменник дробу на
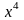 ,
одержимо:
,
одержимо:
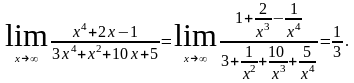
Отже, щоб розкрити невизначеність виду , задану відношенням двох многочленів, потрібно чисельник і знаменник поділити на найвищий степінь x цих многочленів.
3)
Невизначеність виду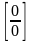 ,
задана відношенням двох многочленів:
,
задана відношенням двох многочленів:

Розкладемо чисельник і знаменник на множники і скоротимо дріб на спільний множник (x-1):
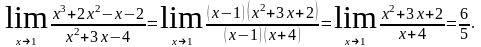
Скорочення
на (х-1) можливе тому, що при означенні
границі
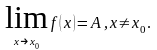 Тобто при
Тобто при
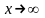
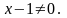
3. Використання повного диференціала до наближених обчислень.
При
досить малому прирості х
аргументу
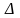 х
диференційованої функції f(x)
приріст у функції
у
буде близький за своєю величиною до
диференціала функції. Тому приріст
функції можна наближено прирівнювати
до диференціала функції
х
диференційованої функції f(x)
приріст у функції
у
буде близький за своєю величиною до
диференціала функції. Тому приріст
функції можна наближено прирівнювати
до диференціала функції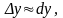 або
або
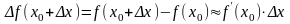 ,
,
якщо позначити х = х - х0, то це ж рівняння приймає вигляд:
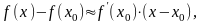 або
або
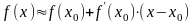 .
Таким чином, для значення де, близьких
до х0,
функцію f
(x)
наближено можна замінити лінійною
функцією. Геометричне це заміні ділянки
кривої y=f(x),
прилеглої до точки (x0,f(x0),
відрізком
дотичної до кривої в цій точці:
.
Таким чином, для значення де, близьких
до х0,
функцію f
(x)
наближено можна замінити лінійною
функцією. Геометричне це заміні ділянки
кривої y=f(x),
прилеглої до точки (x0,f(x0),
відрізком
дотичної до кривої в цій точці:
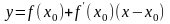 Беручи значення х0
= 0
і обмежуючись малими значеннями х,
одержимо наближену формулу
Беручи значення х0
= 0
і обмежуючись малими значеннями х,
одержимо наближену формулу